一文弄懂梯度下降算法
1、引言
在上一篇文章中,我们介绍了如何使用线性回归和成本损失函数为房价数据找到最拟合的线。不过,我们也看到,测试多个截距值可能既繁琐又低效。在本文中,我们将深入探讨梯度下降算法,这是一种更加强大的技术,可以帮助我们找到完美的截距并进而优化模型。我们将探究其背后的数学原理,看看如何将其应用到线性回归问题中。
闲话少说,我们直接开始吧!
2、梯度下降
梯度下降是一种强大的优化算法,旨在快速有效地找到曲线的最低点。将这一过程形象化的最佳方式就是想象你站在山顶,山谷中有一个装满黄金的宝箱在等着你。

然而,山谷的确切位置却不得而知,因为外面一片漆黑,什么也看不见。此外,你还想赶在其他人之前到达山谷(因为您想独自拥有所有宝藏)。梯度下降算法可以帮助你驾驭地形,高效快速地到达最佳点。在每个点上,它都会告诉你需要走多少步,朝哪个方向走。
同样,梯度下降算法的处理步骤也可以应用于线性回归问题。为了直观地展示寻找最小值的过程,让我们绘制 MSE 曲线。我们已经知道该曲线的方程为:

从上一篇文章中,我们知道问题中的 MSE 方程为:

如果我们把视角放大,就会发现在上式中代入一系列截距值,就能得到一条 MSE 曲线(与我们的山谷相似)。因此,让我们输入 10,000 个截距值,就能得到这样一条曲线:

我们的目标是达到 MSE 曲线的底部,我们可以通过下面的来步骤实现这一目标。
3、步骤一:随机初始化
在这种情况下,我们可以从截距值随机初始化开始,这里假设我们最初猜测的截距值为 0。
4、 步骤二:计算梯度值
曲线在某一点处的梯度值用该点的切线表示(切线是曲线在该点与曲线相切的一种特殊说法)。例如,在 A 点,当截距等于 0 时,MSE 曲线的梯度可用红色切线表示。

为了确定具体梯度值,我们需要运用微积分的知识。具体来说,梯度等于曲线相对于给定点截距的导数,计算公式表示为:

我们据此,计算 MSE曲线在截距为零处的导数如下:

现在,为了求出在A点的梯度,我们将 A 点的截距值代入上式。由于截距 = 0,所以 A 点的导数为:

因此,当截距为0时,梯度值为-190。
注意:当我们接近最佳值时,梯度值将趋近于零。在最佳值处,梯度值等于零。相反,离最佳值越远,梯度值越大
由此我们可以推断,步长应该与梯度有关,因为梯度会告诉我们应该迈小步还是大步。这意味着,当曲线的梯度值接近 0 时,我们就应该迈小步,因为我们已经接近最优值了。而如果梯度较大,我们就应该迈大步,以便更快地达到最优值。
注意:如果我们迈出了超级大的一步,那么我们可能会跳得很大,错过最佳点。因此,我们需要小心谨慎。

5、步骤三:更新
由于我们看到步长和梯度成正比,因此步长是通过梯度乘以一个预先确定的常量值(称为学习率)来确定的:

学习率控制步长的大小,确保步长不会过大或过小。
实际上,学习率通常是一个小正数,即 ≤ 0.001。但对于我们的问题,让我们把它设为 0.1。
因此,当截距为 0 时,计算步长公式为:

根据上述计算出的步长,我们使用以下任何一个等效公式更新截距(又称更改当前位置):

要在这一步中找到新的截距,我们只需要代入相关的值,如下:

求解得到新的截距 = 19。现在将这个值代入MSE 等式,我们会发现截距为 19 时的 MSE = 8064.095。我们又一步就接近了最佳值,降低了 MSE。

即使观察我们的图表,也会发现截距为 19 的新直线比截距为 0 的旧直线更适合我们的数据,如下:

6、步骤四:重复
接着我们使用更新后的截距值来重复步骤 2 和 3。
例如,由于本次迭代的新截距值为 19,因此在步骤 2 之后,我们将计算这一新点的梯度:

我们发现,在截距值 19 处,MSE 曲线的梯度为-152(如下图中红色切线所示)。

接下来,根据步骤 3,我们来计算步长:

随后,更新截距值:

现在,我们可以将截距为 19 的直线与截距为 34.2 的新直线进行比较,如下:

我们可以看到,新的直线更加符合数据的分布。总体而言,MSE 越来越小。

而我们的步长却越来越小:

我们反复重复这一过程,直到趋近于最优解:

当我们向曲线的最小点前进时,我们发现步长越来越小。13 步之后,梯度下降算法估计截距值为 95,这将被确认为 MSE 曲线的最小点。很明显,这种方法比我们在上一篇文章中看到的 "暴力 "方法更有效。
现在我们有了截距的最佳值,线性回归模型就应该是这样:

线性回归方程线可视化是这样的:

最佳拟合线,截距=95,斜率=0.069
最后,回到马克朋友的问题–他的 2400 平方英尺的房子应该卖多少钱?

将 2400 平方英尺的房屋面积代入上式,计算结果如下:

然后就可以了。我们可以告诉我们这位杞人忧天的朋友马克,根据他所在社区的 3 所房子的情况,他应该以 26.06 万美元左右的价格出售自己的房子。
7、 为什么梯度下降有用?
为了说明这一点,请考虑这样一种情况:我们试图到达曲线 C 的最小点,记为 x*。而我们目前在 A 点,位于 x* 的左边:

如果我们求出曲线在 A 点相对于 x 的导数(表示为 dC(x)/dx),会得到一个负值(这意味着梯度是向下倾斜的)。我们还观察到,我们需要向右移动才能到达 x*。因此,我们需要增加 x 才能达到最小值 x*。

由于 dC(x)/dx 为负值,x-𝛂*dC(x)/dx 将大于 x,从而向 x* 移动。
同样,如果我们位于最小点 x* 右侧的 A 点,那么我们会得到一个正梯度(梯度向上倾斜),即 dC(x)/dx。

因此, x-𝛂*dC(x)/dx 将小于 x,从而向 x* 移动。
8、梯度下降什么时候停止?
因此,当某一点的梯度接近 0 或在最小点附近时,步长也将接近 0,表明算法已达到最优解。

当我们接近最小点时,梯度接近 0,因此步长也接近 0
通常,最小步长 = 0.001 或更小

尽管如此,梯度下降法也有一个在终止前的步数限制,称为 “最大步数”。
通常,最大步数 = 1000 或更大
因此,即使步长大于最小步长,如果步数超过最大步数,梯度下降算法也会停止。
9、多个局部最优解
到目前为止,我们一直在处理一条很容易确定最小点的曲线(这类曲线称为凸曲线)。但如果我们有一条不那么漂亮的曲线(技术上又称非凸曲线),看起来像这样呢?

在这里,我们可以看到 B 点是全局最小值(实际最小值),而 A 点和 C 点是局部最小值(可能会被混淆为全局最小值的点,但其实不是)。因此,如果一个函数有多个局部最小值和一个全局最小值,并不能保证梯度下降一定能找到全局最小值。此外,找到哪个局部最小值还取决于初始猜测的位置(如梯度下降的步骤 1 所示)。

以上面这条非凸曲线为例,如果初始猜测点位于block A 或block C,梯度下降算法会宣布最小点分别位于局部最小点 A 或 C,而实际上它应该位于 B。
现在的问题是,我们如何做出正确的初始化猜测?
答案并不简单:从上图中可以看出,如果我们对 x 的最小值猜测是 0,因为它位于图块 A 中,那么它将导致局部最小值 A 的出现。此外,如果可行的话,使用不同的初始化猜测运行算法并比较其结果,可以让我们了解猜测之间是否存在显著差异。这有助于更有效地确定全局最小值。
10、总结
本文重点介绍了如何利用梯度下降法来求解线性回归问题,并给出了详细的图例说明。
您学废了吗?
相关文章:

一文弄懂梯度下降算法
1、引言 在上一篇文章中,我们介绍了如何使用线性回归和成本损失函数为房价数据找到最拟合的线。不过,我们也看到,测试多个截距值可能既繁琐又低效。在本文中,我们将深入探讨梯度下降算法,这是一种更加强大的技术&…...

确认偏差:金融市场交易中的隐形障碍
确认偏差,作为一种深刻影响交易员决策与表现的心理现象,其核心在于个体倾向于寻求与既有信念相符的信息,而自动过滤或轻视与之相悖的资讯。这种认知偏见严重扭曲了交易者的决策过程,导致他们过分依赖符合既有观念的数据࿰…...

Linux系统之部署linkding书签管理器
Linux系统之部署linkding书签管理器 一、linkding介绍1.1 linkding简介1.2 linkding特点二、本地环境介绍2.1 本地环境规划2.2 本次实践介绍三、检查本地环境3.1 检查本地操作系统版本3.2 检查系统内核版本四、部署Node.js 环境4.1 下载Node.js安装包4.2 解压Node.js安装包4.3 …...
springcloud-gateway 路由加载流程
问题 Spring Cloud Gateway版本是2.2.9.RELEASE,原本项目中依赖服务自动发现来自动配置路由到微服务的,但是发现将spring.cloud.gateway.discovery.locator.enabledfalse 启动之后Gateway依然会将所有微服务自动注册到路由中,百思不得其解&a…...

双减期末考试成绩怎么公布?
考试一直是衡量学生学习成果的重要手段。不过,随着"双减"政策的实施,我们就不得不重新审视传统的成绩公布方式。期末考试成绩,这个曾经让无数学生心跳加速的数字,如今该如何以一种更加合理、公正的方式呈现给学生和家长…...
2, 搭建springCloud 项目 测试demo
上篇文章 新建了父依赖服务,这篇文章就建两个demo测试服务。 因为后面需要做服务间的通讯测试,所以至少需要建两个服务 建个子模块 同样的方式建连个demo服务 给java 和resources目录添加属性 在resources目录下建一个applications.yml文件,…...

RabbitMQ消息积压比较厉害,然后突然丢弃
RabbitMQ中的消息积压陡降通常表明某些突发事件或操作已经显著减少了队列中的消息数量。这种现象可能由多种原因引起,以下是一些可能的原因及其解释: 消费者处理速度突然增加 原因: 你的消费者(消费者应用或服务)可能在某个时间点…...
QT中的样式表.qss文件
一、前言 qt中样式表的改变有几种方法,第一种就是直接在ui界面对应的组件右键修改样式表,还有一种就是直接在程序里面修改样式表,我知道的还有一种就是qss文件,这个文件就是将在程序中写的修改样式表的语句写道qss文件中ÿ…...

HTML图片链接缓存问题解决
关于解决HTML使用图片链接出现的缓存问题处理 1、项目上明明替换了图片却没发现更新,得去浏览器设置清除浏览器缓存或者其它一些操作才能解决,这也太麻烦了!加载过一次不会再加载第二次,其实这时候就存在浏览器图片缓存情况&…...
一个人 三个月 干了二十万
相信很多人是被这个标题吸引进来的,但我并不是标题党,我也很讨厌标题党,这篇文章也不在乎流量,更多的是想记录下。 出来创业三个多月了,给大家汇报一下这段时间的业绩吧。一个人,三个多月,干了…...

设计模式之【工厂模式、适配器模式】
工厂模式(Factory Pattern) 定义: 工厂模式是一种创建型设计模式,它提供了一个创建对象的接口,但由子类决定要实例化的类是哪一个。工厂方法使一个类的实例化延迟到其子类。 主要类型: 简单工厂模式&…...

云计算:重塑数字时代的基石
目录 一、引言 二、云计算的定义与特点 三、云计算的发展历程 四、云计算的应用场景 五、云计算面临的挑战 六、云计算的未来发展趋势 七、结语 一、引言 随着信息技术的飞速发展,云计算已经逐渐渗透到我们生活的方方面面。从个人用户的在线存储、在线办公&…...
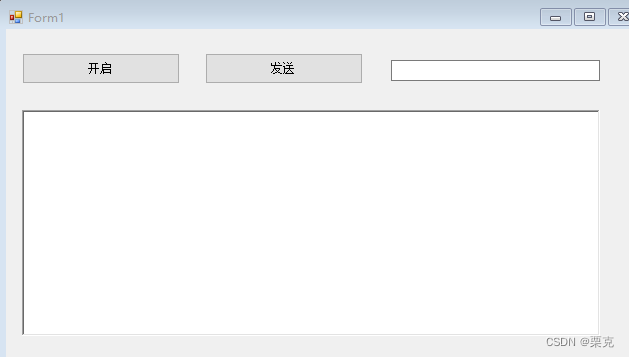
C# SocketUDP服务器,组播
SocketUDP 自己即是服务器又是客户端 ,在发消息只需要改成对方ip和端口号即可 前提对方必须开启服务器 socket.Bind(new IPEndPoint(IPAddress.Parse("192.168.107.72"), 8080)); 控件:Button,TextBox,RichTextBox 打开自己服务器 public…...

上市公司绿色投资者原始数据+计算代码(2008-2022年)
数据简介:“绿色”信号,意味着潜在环境风险更低,从而绿色投资者降低了对绿色债券的风险补偿要求,推动了信用利差的收窄。因此,绿色投资者会通过投资者风险意识影响债券信用风险。绿色投资者在推动企业绿色可持续发展方…...
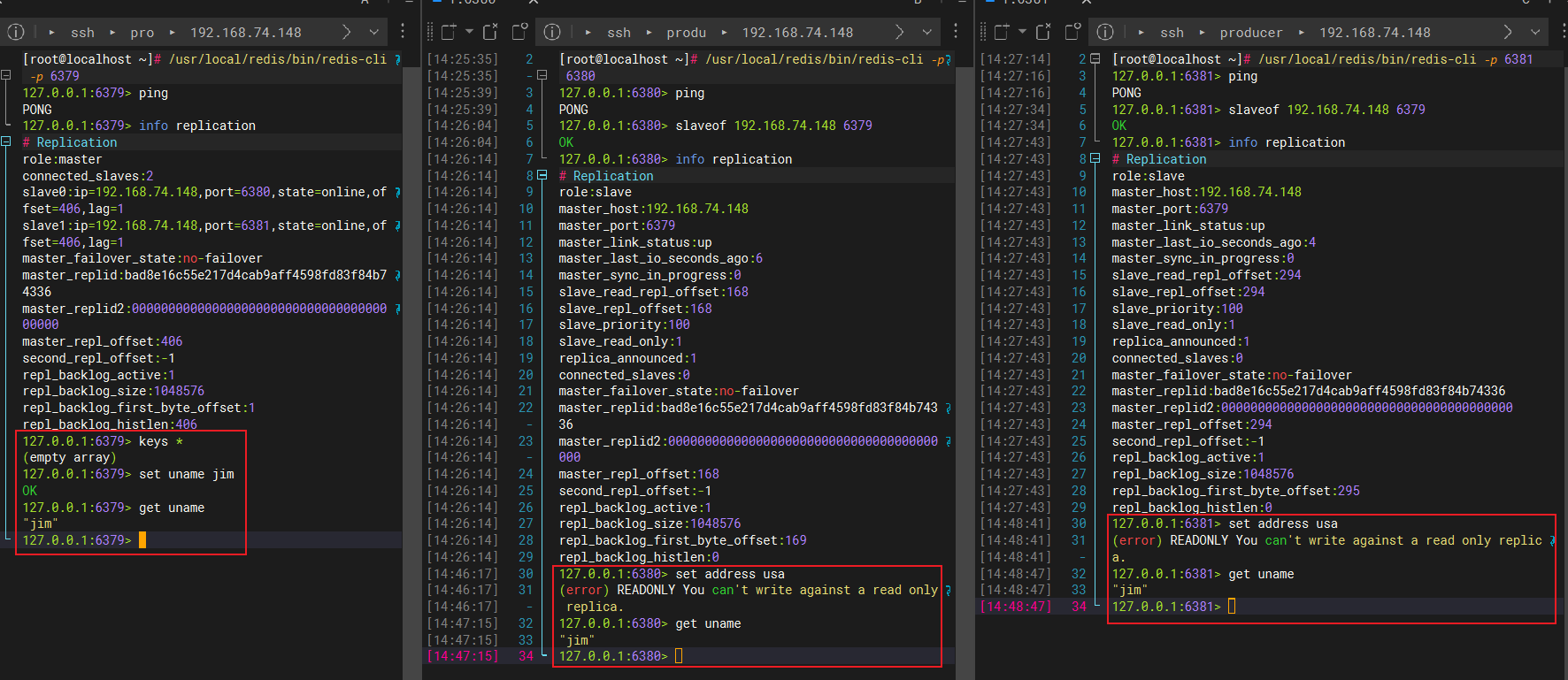
Redis-主从复制-测试主从模式下的读写操作
文章目录 1、在主机6379写入数据2、在从机6380上写数据报错3、从机只能读数据,不能写数据 1、在主机6379写入数据 127.0.0.1:6379> keys * (empty array) 127.0.0.1:6379> set uname jim OK 127.0.0.1:6379> get uname "jim" 127.0.0.1:6379>…...
Linux系统应用与设置(3):串口调试(minicom)
目录 1. 简述 2. 安装minicom 3. 配置串口参数 4. 打开相应的通信端口 5. 设置 6. 发送字符数据 7. 发送HEX(十六进制) 1. 简述 在Linux系统中,minicom是一个功能强大的串口通信工具,可用于与外部设备进行字符和HEX数据的收…...
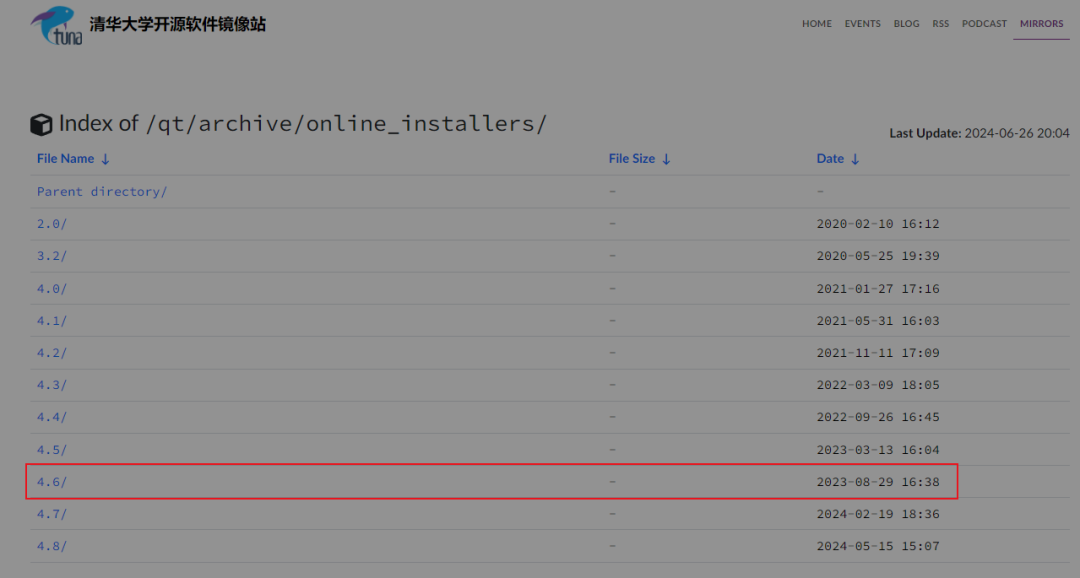
Qt | windows Qt6.5.3安卓环境搭建成功版(保姆级教程)
01、第一章 Qt6.5.3安装 资源 Qt 国内下载地址清华大学开源软件镜像站https://mirrors.tuna.tsinghua.edu.cn/qt/archive/online_installers/Qt 阿里云盘下载Qt 安卓开发https://www.alipan.com/s/kNaues6CHaG点击链接保存,或者复制本段内容,打开「阿里云盘」APP ,无需下载极…...

Chrome Extension如何让work flow在页面刷新、跳转继续执行任务
从Electron到Chrome Extension:流程自动化的跨平台探索 在之前的项目中,我使用Electron成功实现了一个流程自动化应用,它极大地提高了工作效率。然而,当面对Chrome扩展程序(Extension)的需求时,我意识到需要一种新的策略来应对浏览器环境下的限制。特别是Chrome Extens…...
数据库调优厂商 OtterTune 宣布停止运营
昨天刷到消息,得知数据库优化厂商 OtterTune 停止了运营。OtterTune 的成员主要来自 CMU Andy Pavlo 教授领导的数据库实验室。公司正式成立于 2021 年 5 月,融资了 1450 万美金。 按照 Andy 教授的说法,公司是被一个收购 offer 搞砸了。同时…...

4、面向对象-typescript
从面向过程转向面向对象,是一个由简易到复杂的过程,主要更多的考虑到对象的属性,方法,行为等。 一、类,对象 类:更偏向于模板,属于抽象类型,指向大类或泛指。 对象ÿ…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
