OpenGL3.3_C++_Windows(22)
材质:
- 决定物体在渲染过程中最终视觉呈现的关键因素之一,它通过一系列光学(投光物)和物理参数(反光度,反照率、金属度,折射率……)准确模拟现实世界中的材料特性,从而增强虚拟环境的逼真度和沉浸感。
float spec = pow(max(dot(viewDir, reflectDir), 0.0), material.shininess);首先看一下冯氏光照模型镜面反射的计算:
- 将(视线,反射光线)点乘,角度越小(0——90)cos越大,
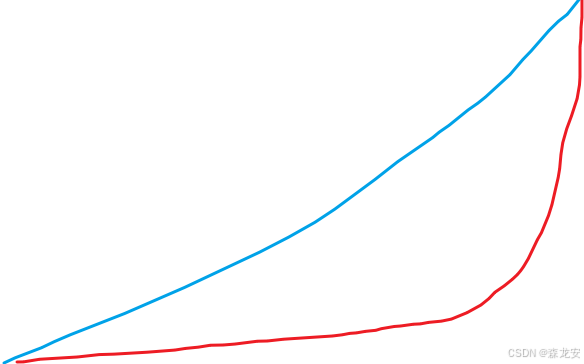
- 通过max控制结果非负,当(>90)度,结果为负值,取0,【0——1】
- 通过pow,取反光度^幂,当反光度越高,函数的曲线会陡增的越明显
- 反光度越高,反射光的能力越强,散射得越少,高光点就会越小
注意:
- 物体反光度很高时,没有什么大影响,大多数观察方向与反射方向的pow结果都很小,只有一小部分很亮,大部分都是暗的,这种一个小圆圈点的断层几乎每什么影响
- 物体反光度很低时,高光 的范围会很大,当(视线,反射光线)(>90)度,结果为负值取0,会出现了很大的的断层(亮部--暗部)
- 对于漫反射angle为负数是正确的,(入射光线,法线)点乘,如果>90度,光线位于物体片段的下方,确实不会产生漫反射结果。
Blinn-Phong着色模型:(解决了断层问题)
- 对镜面光模型的处理上有一些不同,不再依赖于反射向量
-
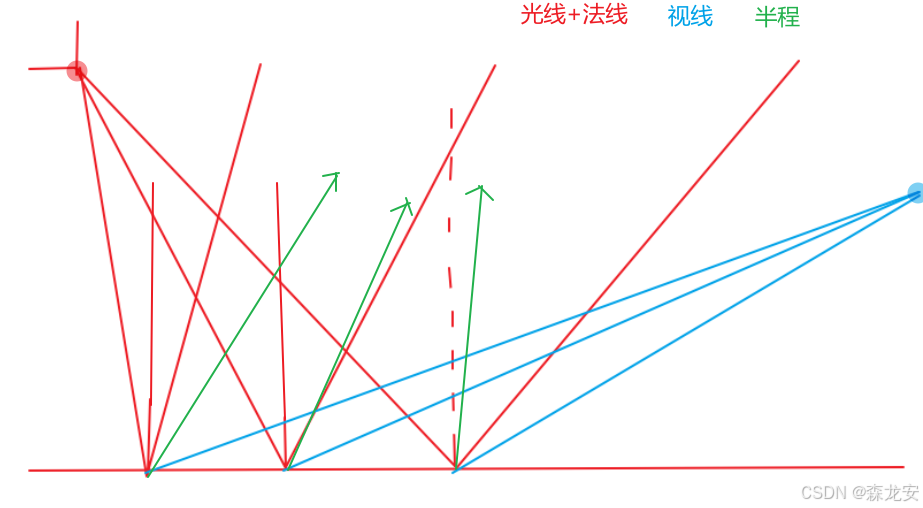
半程向量:
- 即光线与视线夹角一半方向上的一个单位向量,当半程向量与法线向量越接近时,镜面光分量就越大。
- 当视线正好与反射向量对齐时,半程向量就会与法线完美契合,当观察者视线越接近于原本反射光线的方向时,镜面高光就会越强
- 半程向量与表面法线之间的夹角都不会超过90度:(除非光源在表面以下)
- 首先如果视线在表面下,我们看不到片段,所以不必关心它的最终结果,光源在表面以下会照射底面,而照射不到上面,所以视线和光线都应在表面上方。而法线距离半程的最大值,为视线和光线都为0 / 180 度时
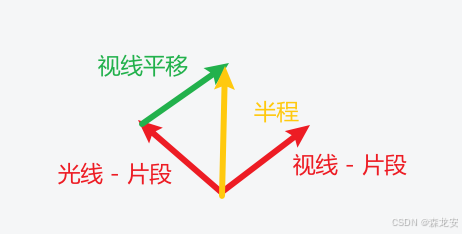
计算半程:
vec3 halfwayDir = normalize(lightDir + viewDir);
spec = pow(max(dot(normal, halfwayDir), 0.0), 16.0);-
向量相加(入射光线 + 视线 ) / |(入射光线 + 视线 )|正规化(只关心半程向量方向,不关系长度)
-
计算Blinn-Phong的镜面光:……只需要dot(半程,法线)……
- 半程向量与表面法线的夹角通常会小于观察与反射向量的夹角(意味着相同片段位置,dot结果更大,pow结果更大,高光散射范围广):
- 所以应将镜面反光度设置更高一点,让高光范围更集中
相关文章:

OpenGL3.3_C++_Windows(22)
材质: 决定物体在渲染过程中最终视觉呈现的关键因素之一,它通过一系列光学(投光物)和物理参数(反光度,反照率、金属度,折射率……)准确模拟现实世界中的材料特性,从而增…...
electron-builder 打包过慢解决
报错内容如下 > 6-241.0.0 build > electron-builder • electron-builder version24.13.3 os10.0.22631 • loaded configuration filepackage.json ("build" field) • writing effective config filedist\builder-effective-config.yaml • pack…...

leetcode226反转二叉树
本文主要讲解反转二叉树的要点与细节,按照步骤思考更方便理解 c和java代码如下,末尾 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 具体要点: 1. 首先我们要理解题意, 反转二叉树具体…...
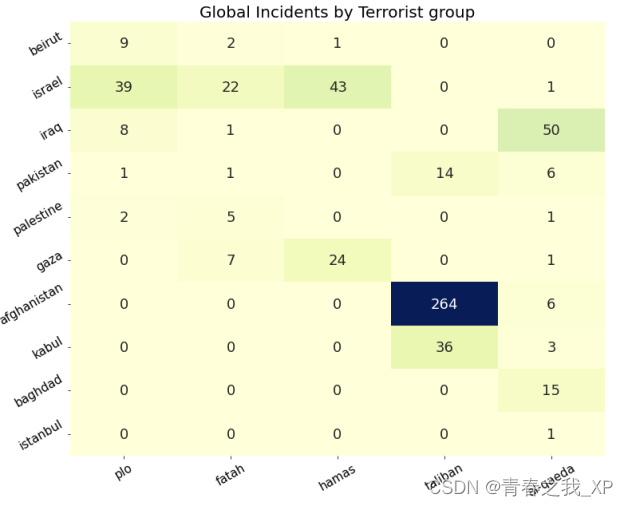
【自然语言处理系列】探索NLP:使用Spacy进行分词、分句、词性标注和命名实体识别,并以《傲慢与偏见》与全球恐怖活动两个实例文本进行分析
本文深入探讨了scaPy库在文本分析和数据可视化方面的应用。首先,我们通过简单的文本处理任务,如分词和分句,来展示scaPy的基本功能。接着,我们利用scaPy的命名实体识别和词性标注功能,分析了Jane Austen的经典小说《傲…...

【Rust】function和methed的区别
文章目录 functionmethedAssociated Functions 参考资料 一句话总结: function和methed很多都是相同的。 不同点在于: methed定义在结构体里面,并且它的第一个参数肯定是self,代表结构体实例。方法需要用实例名.方法名调用当然结…...

python基础语法 003-4 数据类型集合
1 集合 1.1 什么是集合 什么是集合?ANS:集合set是一个无序的不重复元素序列集合怎么表示?ANS: {} , 用逗号隔开打印元组类型,type()一个元素的集合怎么表示?:ANS:存储多种类型{"a", 1} """…...

Vue如何引用组件
在 Vue.js 中,你可以通过几种方式引用组件: 全局注册 在 main.js 或你的主入口文件中,你可以使用 Vue.component() 方法来全局注册一个组件。这意味着这个组件可以在你的 Vue 应用的任何地方使用。 import MyComponent from ./components/…...

vue3中省市区联动在同一个el-form-item中咋么设置rules验证都不为空的效果
在开发中出现如下情况,在同一个el-form-item设置了省市区三级联动的效果 <el-form-item label"地区" prop"extraProperties.Province"><el-row :gutter"20"><el-col :span"12"><el-select v-model&qu…...
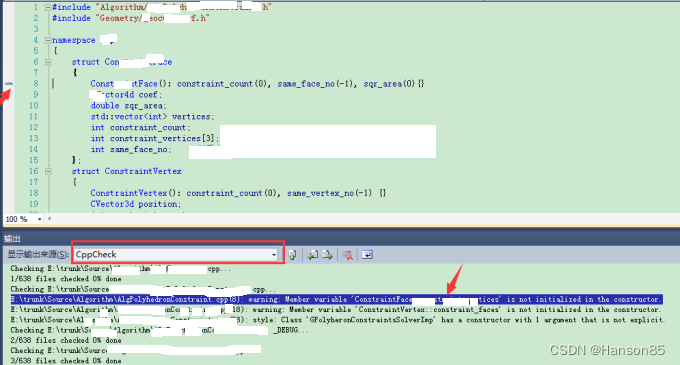
如何集成CppCheck到visual studio中
1.CPPCheck安装 在Cppcheck官方网站下载最新版本1.70,官网链接:http://cppcheck.sourceforge.net/ 安装Cppcheck 2.集成步骤 打开VS,菜单栏工具->外部工具->添加,按照下图设置,记得勾选“使用输出窗口” 2.…...

GWO-CNN-SVM,基于GWO灰狼优化算法优化卷积神经网络CNN结合支持向量机SVM数据分类(多特征输入多分类)
GWO-CNN-SVM,基于GWO灰狼优化算法优化卷积神经网络CNN结合支持向量机SVM数据分类(多特征输入多分类) 1. GWO灰狼优化算法 灰狼优化算法(Grey Wolf Optimizer, GWO)是一种启发式优化算法,模拟了灰狼群体的社会行为,包…...

Go-知识测试-工作机制
Go-知识测试-工作机制 生成test的maintest的main如何启动case单元测试 runTeststRunnertesting.T.Run 示例测试 runExamplesrunExampleprocessRunResult 性能测试 runBenchmarksrunNtesting.B.Run 在 Go 语言的源码中,go test 命令的实现主要在 src/cmd/go/internal…...

【小程序静态页面】猜拳游戏大转盘积分游戏小程序前端模板源码
猜拳游戏大转盘积分游戏小程序前端模板源码, 一共五个静态页面,首页、任务列表、大转盘和猜拳等五个页面。 主要是通过做任务来获取积分,积分可以兑换商品,也可用来玩游戏;通过玩游戏既可能获取奖品或积分也可能会消…...

JupyterServer配置
1. 安装jupyter pip install jupyter -i https://pypi.tuna.tsinghua.edu.cn/simple --default-timeout1000 2. 生成配置 jupyter notebook --generate-config 3. 修改配置,设置密码 获取密码的方式:命令行输入python后,用以下方式获…...
:MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS)
信息检索(57):MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS
MINIMIZING FLOPS TO LEARN EFFICIENT SPARSE REPRESENTATIONS 摘要1 引言2 相关工作3 预期 FLOPS 次数4 我们的方法5 实验6 结论 发布时间(2020) 最小化 Flop 来学习高效的稀疏表示 摘要 1)学习高维稀疏表示 2)FLOP 集成到损失…...

Python 面试【中级】
欢迎莅临我的博客 💝💝💝,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...
[Open-source tool]Uptime-kuma的簡介和安裝於Ubuntu 22.04系統
[Uptime Kuma]How to Monitor Mqtt Broker and Send Status to Line Notify Uptime-kuma 是一個基於Node.js的開軟軟體,同時也是一套應用於網路監控的開源軟體,其利用瀏覽器呈現直觀的使用者介面,如圖一所示,其讓使用者可監控各種…...

【2024最新华为OD-C/D卷试题汇总】[支持在线评测] 灰度图像恢复(100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C/D卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 …...

leetcode494. 目标和
1.思想方法 2.代码 class Solution { public int findTargetSumWays(int[] nums, int target) {int sum 0;for(int num : nums)sum num;if(sum < Math.abs(target) || (targetsum)%2 ! 0)return 0;int x (targetsum) / 2,n nums.length;//基于滚动数组的方法int[] dp…...

数据结构简介
在容器的基础之上,java引入了数据结构的概念。数据结构可以简单地理解成是一个以特定的布局方式来存储数据的容器。但是我个人觉得这种理解方式不太合理,根据我们学的数据结构的内容,我更倾向于数据结构是数据在容器中的布局方式,…...
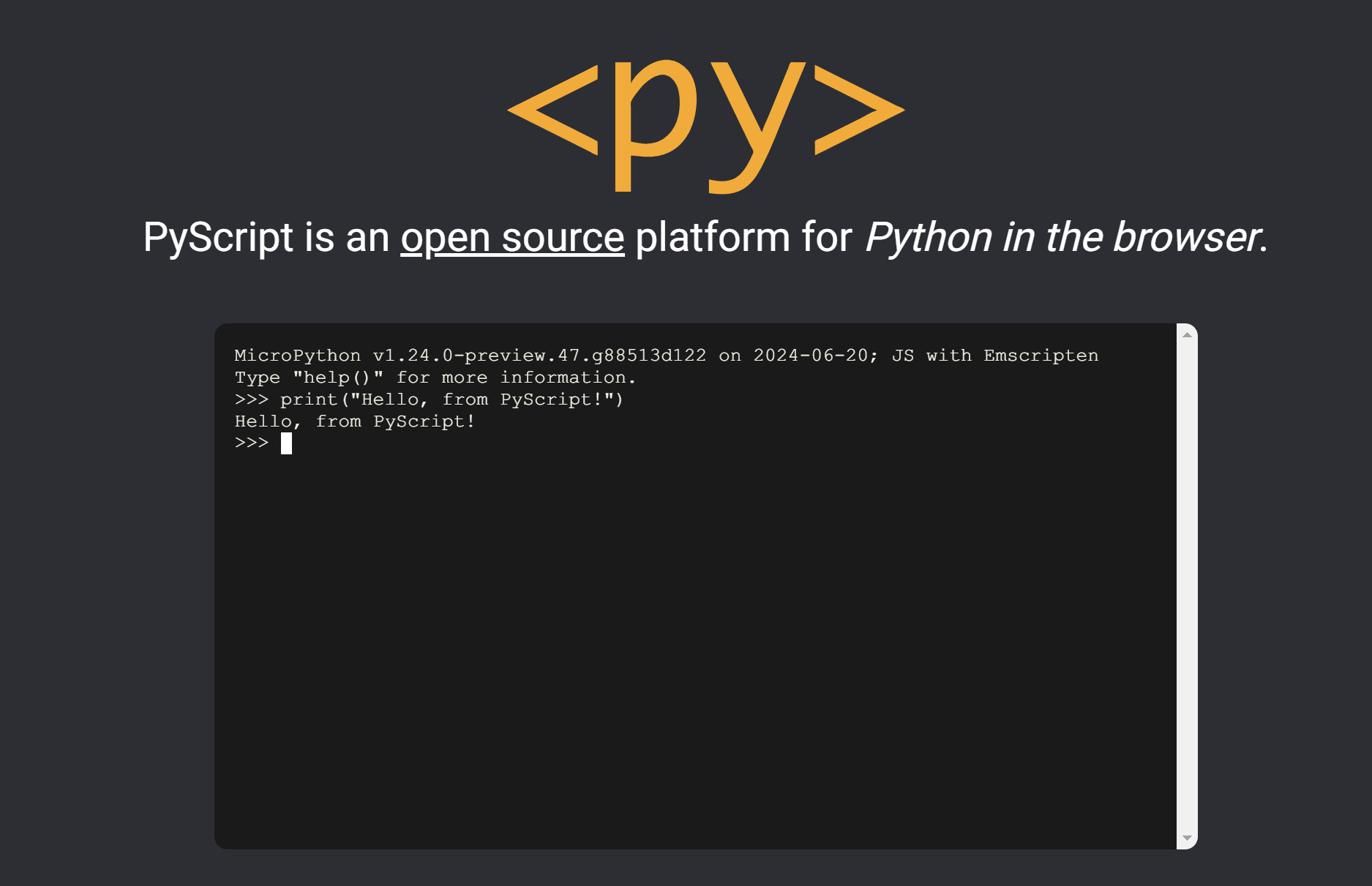
PyScript:在浏览器中释放Python的强大
PyScript:Python代码,直接在网页上运行。- 精选真开源,释放新价值。 概览 PyScript是一个创新的框架,它打破了传统编程环境的界限,允许开发者直接在浏览器中使用Python语言来创建丰富的网络应用。结合了HTML界面、Pyo…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
