Open3D 删除点云中重复的点
相关文章：
Open3D 删除点云中重复的点
目录 一、算法原理1、重叠点2、主要函数二、代码实现三、结果展示本文由CSDN点云侠原创，原文链接。如果你不是在点云侠的博客中看到该文章，那么此处便是不要脸的爬虫与GPT。 一、算法原理 1、重叠点 原始点云克隆一份 构造重叠区域 合并点云获得重叠点 2、主要…...
填报志愿选专业是兴趣重要还是前景重要？
进行专业评估，找到一个适合自己的专业是一件非常困难的事情。在进行专业选择时，身上理想化色彩非常严重的人，会全然不顾及他人的劝阻，义无反顾的以兴趣为主，选择自己热爱的专业。一些较多考虑他人建议，能听…...
python开发基础——day9 函数基础与函数参数
一、初识函数(function) 编程函数!数学函数，里面的是逻辑，功能，而不是套公式 编程函数的作用实现特定操作的一段代码 你现在请客，每个人都点同样的一份吃的，请100个人 1.薯条 2.上校鸡块 3.可乐 那…...
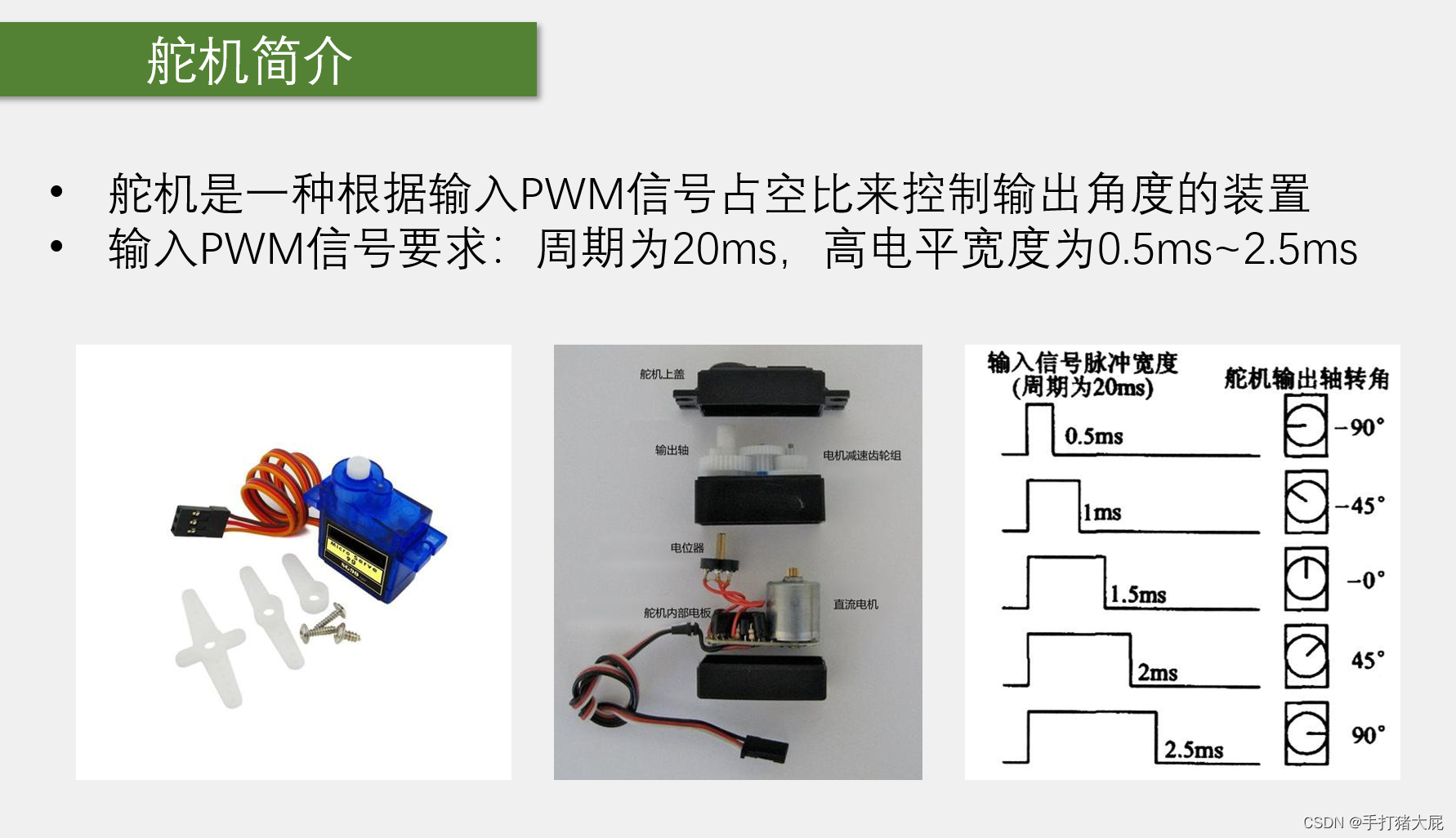
STM32——使用TIM输出比较产生PWM波形控制舵机转角
一、输出比较简介： 只有高级定时器和通用寄存器才有输入捕获/输出比较电路，他们有四个CCR（捕获/比较寄存器），共用一个CNT（计数器），而输出比较功能是用来输出PWM波形的。 红圈部分…...
第十五章 集合（set）（Python）
文章目录 前言一、集合 前言 集合（set）是一个无序的不重复元素序列。 一、集合 set {1, 2, 3, 4}...
面试-javaIO机制
1.BIO BIO：是传统的javaIO以及部分java.net下部分接口和类。例如，socket,http等，因为网络通信同样是IO行为。传统IO基于字节流和字符流进行操作。提供了我们最熟悉的IO功能，譬如基于字节流的InputStream 和OutputStream.基于字符流…...
在.NET Core中，config和ConfigureServices的区别和作用
在.NET Core中，config和ConfigureServices是两个不同的概念，它们在应用程序的启动和配置过程中扮演着不同的角色。 ConfigureServices：这是ASP.NET Core应用程序中的一个方法，位于Startup类的内部。它的作用是配置依赖注入(DI)容器…...
App Inventor 2 如何实现多个定时功能？
1、可以使用多个“计时器”组件。 2、也可以用一个计时器，定时一分钟。也就是一分钟就会触发一次事件执行，定义一个全局数字变量，在事件中递增，用逻辑判断这个变量的值即可完成多个想要定时的任务(о∀о) 代码块请参考…...
技术驱动的音乐变革：AI带来的产业重塑
📑引言 近一个月来，随着几款音乐大模型的轮番上线，AI在音乐产业的角色迅速扩大。这些模型不仅将音乐创作的门槛降至前所未有的低点，还引发了一场关于AI是否会彻底颠覆音乐行业的激烈讨论。从初期的兴奋到现在的理性审视࿰…...
重生之我要学后端0--HTTP协议和RESTful APIs
http和RESTful APIs HTTP协议RESTful APIs设计RESTful API设计实例 HTTP协议 HTTP（超文本传输协议）是用于分布式、协作式和超媒体信息系统的应用层协议。它是网页数据通讯的基础。工作原理简述如下： 客户端请求（Request…...
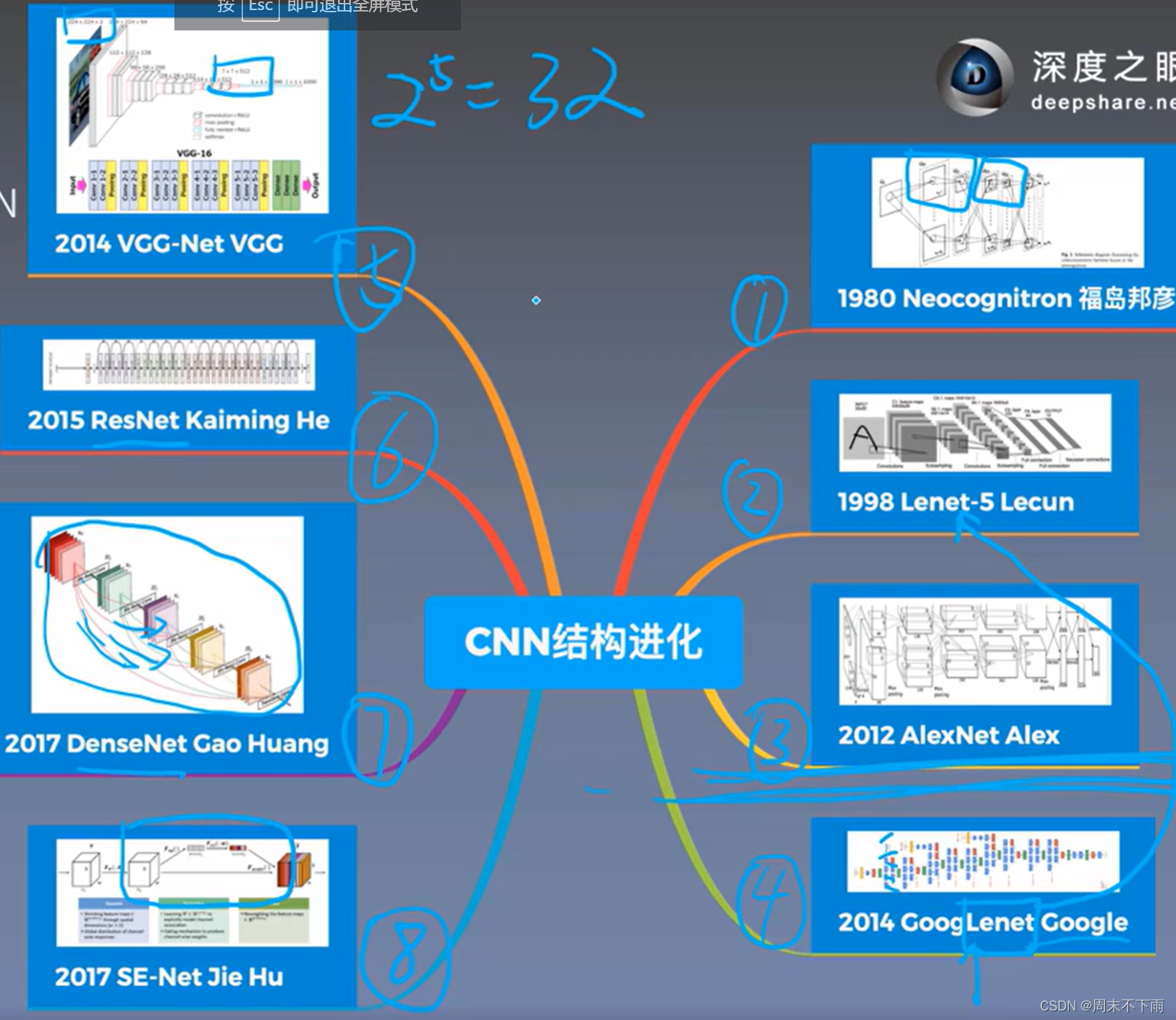
深度之眼（二十八）——神经网络基础知识（三）-卷积神经网络
文章目录 一、前言二、卷积操作2.1 填充（padding）2.2 步长2.3 输出特征图尺寸计算2.4 多通道卷积 三、池化操作四、Lenet-5及CNN结构进化史4.1 Lenet-5 一、前言 卷积神经网络–AlexNet(最牛)-2012 Lenet-5-大规模商用（1989） 二、…...
AI Infra简单记录
向量数据库的作用 1. 在AI大模型训练过程中，向量数据库可以有效提升数据检索、特征提取等任务的效率。 2、在AI大模型推理过程中，向量数据库为大模型提供外挂知识库，提升模型时效性与准确性，提供缓存能力，减少调用开…...
三英战吕布 | 第5集 | 温酒斩华雄 | 竖子不足与谋 | 三国演义 | 逐鹿群雄
🙋大家好！我是毛毛张! 🌈个人首页： 神马都会亿点点的毛毛张 📌这篇博客分享的是《三国演义》文学剧本第Ⅰ部分《群雄逐鹿》的第5️⃣集《三英战吕布》的经典语句和文学剧本全集台词 文章目录 1.经典语句2.文学剧本台…...
【C语言】自定义类型：结构体
目录 1. 结构体类型的声明 1.1. 结构的一般声明 1.2. 结构的特殊声明 2. 结构体变量的创建和初始化 3. 结构体的自引用 4. 结构体内存对齐 4.1. 对其规则（面试考点） 4.2. 为什么存在内存对齐？ 4.2.1. 平台原因（移植…...
算法金 | 决策树、随机森林、bagging、boosting、Adaboost、GBDT、XGBoost 算法大全
大侠幸会，在下全网同名「算法金」 0 基础转 AI 上岸，多个算法赛 Top 「日更万日，让更多人享受智能乐趣」 决策树是一种简单直观的机器学习算法，它广泛应用于分类和回归问题中。它的核心思想是将复杂的决策过程分解成一系列简单的决…...
[每周一更]-(第103期)：GIT初始化子模块
文章目录 初始化和更新所有子模块分步骤操作1. 克隆包含子模块的仓库2. 初始化子模块3. 更新子模块 查看子模块状态提交子模块的更改处理子模块路径错误的问题 该问题的缘由是因为：在写某些代码的时候，仓库中有些文件夹，只提交了文件夹名称到…...
单例模式---线程安全实现
文章目录 1.单例模式的特点😊2.单例模式两种实现🤣🤗😊2.1 饿汉式2.2 懒汉式 3.传统单例模式的线程安全问题4.解决方法4.1静态局部变量4.2加锁4.3双重检查锁（DCL）4.4pthread_once 1.单例模式的特点…...
Agent技术在现代软件开发与应用中的探索
一、引言 随着计算机科学的快速发展，Agent技术作为人工智能和分布式计算领域的重要分支，已经渗透到软件开发的各个方面。Agent技术通过赋予软件实体自主性和交互性，使得软件系统能够更加智能、灵活地响应环境变化和用户需求。本文将对Agent技…...
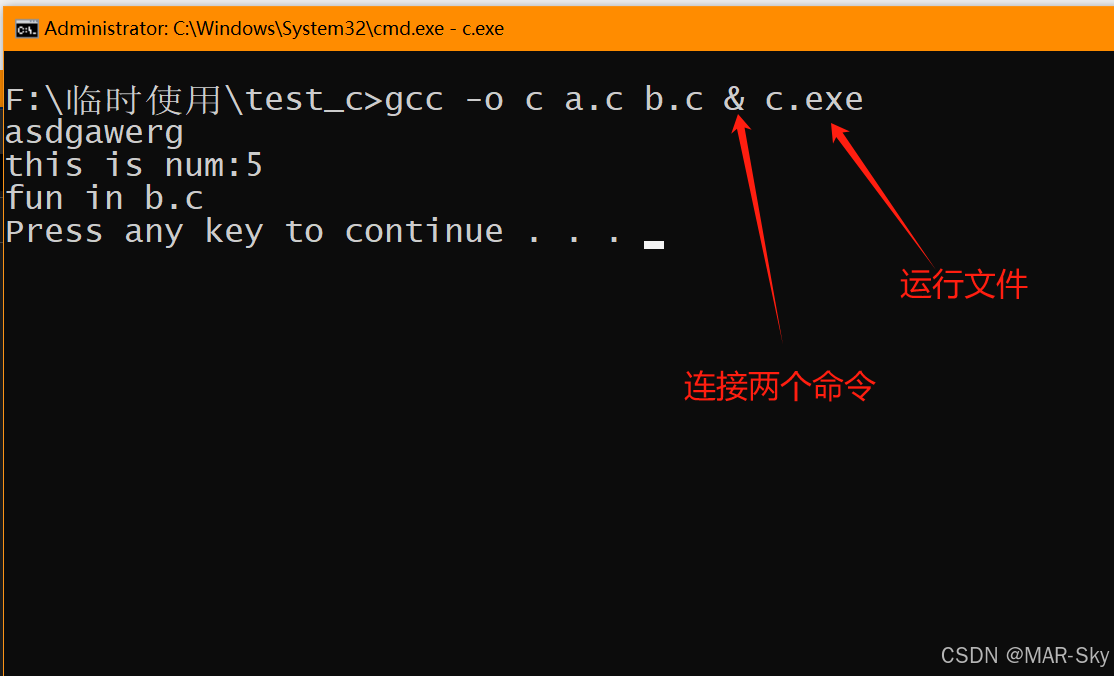
c语言中extern定义和引用其他文件的变量，（sublime text）单独一个文件编译不会成功
关键字extern的作用 这个很常见的都知道是定义一个外部变量或函数，但并不是简单的建立两个文件，然后在用extern 定义在另一个非最初定义变量的文件里 区分文件和编译运行的文件 例如，一个文件夹里有文件a.c和文件b.c,在sublime text中直接…...
时序数据中的孤立野点、异常值识别及处理方法
目录 参考资料 对时序数据做差分； 参考资料 [1] 离群点（孤立点、异常值）检测方法 2017.6；...
高等数学（下）题型笔记（八）空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...
七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
招商蛇口 | 执笔CID，启幕低密生活新境
作为中国城市生长的力量，招商蛇口以“美好生活承载者”为使命，深耕全球111座城市，以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子，招商蛇口始终与城市发展同频共振，以建筑诠释对土地与生活的…...
Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时，显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
【无标题】湖北理元理律师事务所：债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域，专业机构的核心价值不仅在于减轻债务数字，更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明，合法债务优化需同步实现三重平衡： 法律刚性（债…...
全面解析数据库：从基础概念到前沿应用
在数字化时代，数据已成为企业和社会发展的核心资产，而数据库作为存储、管理和处理数据的关键工具，在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理，到社交网络的用户数据存储，再到金融行业的交易记录处理&a…...
Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了，很多小伙伴想体验鸿蒙电脑版操作系统，可惜，鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机，来体验大家心心念念的鸿蒙系统啦！注意：虚拟…...
多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式，给定一个隐函数关系： F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标： 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...
【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud（一）Springcloud五大组件（二）服务注册和发现1、Eureka2、Nacos （三）负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...
统计学（第8版）——统计抽样学习笔记（考试用）
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征（均值、比率、总量）控制抽样误差与非抽样误差 解决的核心问题 在成本约束下，用少量样本准确推断总体特征量化估计结果的可靠性（置…...