240629_昇思学习打卡-Day11-Vision Transformer中的self-Attention
240629_昇思学习打卡-Day11-Transformer中的self-Attention
根据昇思课程顺序来看呢,今儿应该看Vision Transformer图像分类这里了,但是大概看了一下官方api,发现我还是太笨了,看不太明白。正巧昨天学SSD的时候不是参考了太阳花的小绿豆-CSDN博客大佬嘛,今儿看不懂就在想,欸,这个网络大佬讲没讲,就去翻了下,结果还真给我找到了,还真讲过,还有b站视频,讲的贼好,简直就是茅厕顿开,这里附大佬的b站首页霹雳吧啦Wz的个人空间-霹雳吧啦Wz个人主页-哔哩哔哩视频 (bilibili.com),强烈建议去看,附本期链接Transformer中Self-Attention以及Multi-Head Attention详解_哔哩哔哩_bilibili,记得给大佬三连,有能力的给大佬充充电(本人已充)。
本文就大佬所讲内容、查阅资料、昇思api及结合自己理解进行记录。
前言
在了解Vision Transformer之前,我们需要先了解一下Transformer,Transformer最开始是应用在NLP领域的,拿过来用到Vision中就叫Vision Transformer。而这里要提到的,就是Transformer中的self-Attention(自注意力)和Multiple-Head Attention(多头注意力)。
用在NLP领域中用到的注意力机制举例,一般为Encoder-Decoder框架,比如中英翻译,输入的英文是Source,我们要获取到的是Target(中文翻译),Attention机制就发生在Target的元素Query和Source中的所有元素之间,其同时关注自身和目标值。
而这里说的自注意力机制只关注自身,比如Source中会有一个注意力机制,Target中会有一个注意力机制,他两是没有关系的。
还是用中英翻译举例,注意力机制的查询和键分别来自于英文和中文,通过查询(Query)英文单词,去匹配中文汉字的键(Key),自注意力机制只关注自己一个语言,可以理解为:”我喜欢“后面可以跟”你“,也可以跟”吃饭“。
1)如果查询和键是同一组内的特征,并且相互做注意力机制,则称为自注意力机制或内部注意力机制。
2)多头注意力机制的多头表示对每个Query和所有的Key-Value做多次注意力机制。做两次,就是两头,做三次,就是三头。这样做的意义在于获取每个Query和所有的Key-Value的不同的依赖关系。
3)自注意力机制的优缺点简记为【优点:感受野大。缺点:需要大数据。】
以下是关于这两个自注意力机制的官方公式,很复杂也很难理解,但现在别盯着他不放,先慢慢往下看,这篇就是说明这个公式及其过程:

Self-Attention
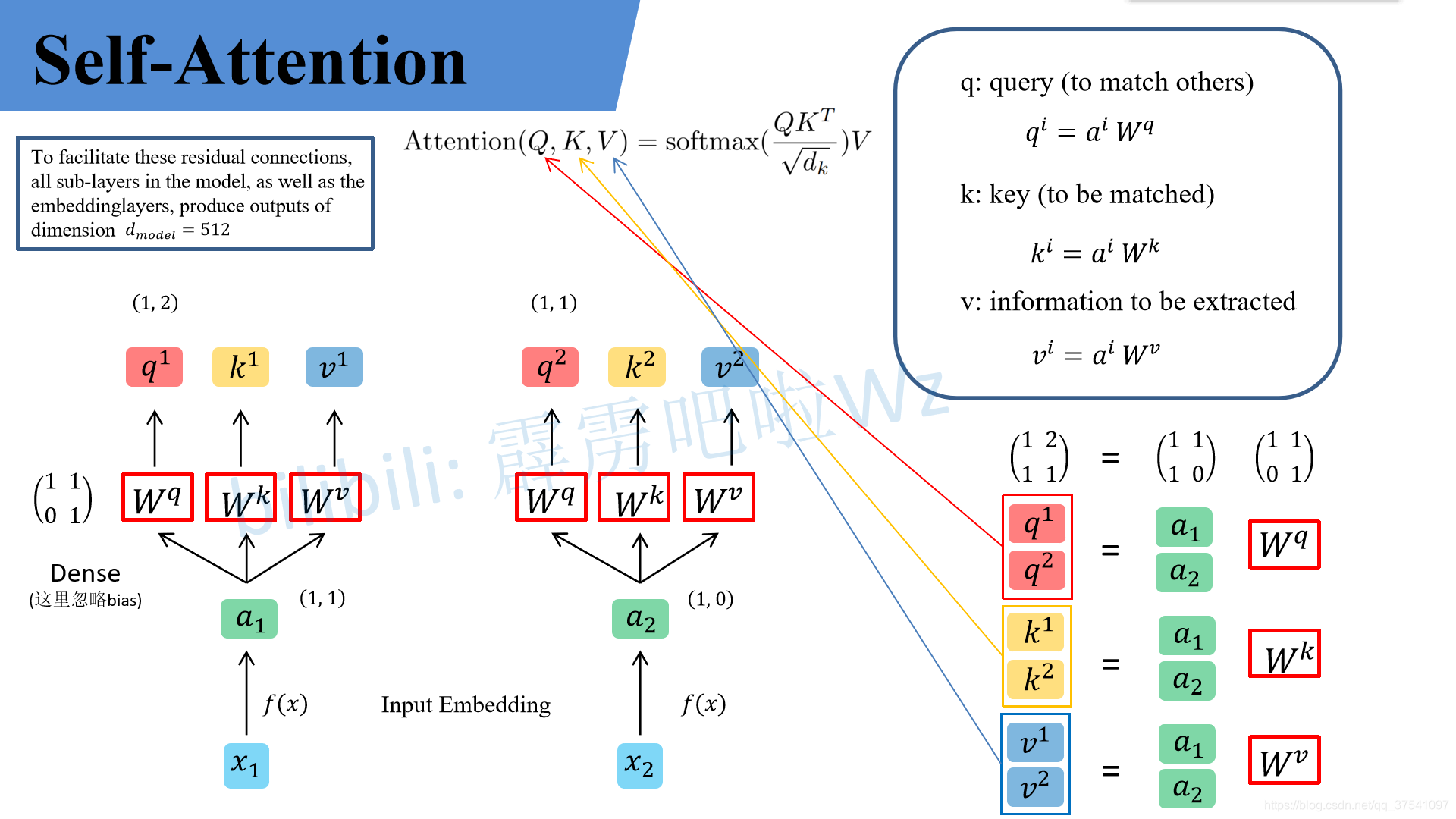
我们先说明白这里面这些符号都是干啥的,或者求出来用来干啥的,避免看半天还一头雾水:
q代表query,后续会去和每一个k进行匹配
k 代表key,后续会被每个q匹配
v 代表从a中提取得到的信息,后续会和q和k的乘积进行运算
d是k的维度
后续q 和k匹配的过程可以理解成计算两者的相关性,相关性越大对应v的权重也就越大
简单来说,最初的输入向量首先会经过Embedding层映射成Q(Query),K(Key),V(Value)三个向量,由于是并行操作,所以代码中是映射成为dim x 3的向量然后进行分割,换言之,如果你的输入向量为一个向量序列(𝑥1,𝑥2,𝑥3),其中的𝑥1,𝑥2,𝑥3都是一维向量,那么每一个一维向量都会经过Embedding层映射出Q,K,V三个向量,只是Embedding矩阵不同,矩阵参数也是通过学习得到的。这里大家可以认为,Q,K,V三个矩阵是发现向量之间关联信息的一种手段,需要经过学习得到,至于为什么是Q,K,V三个,主要是因为需要两个向量点乘以获得权重,又需要另一个向量来承载权重向加的结果,所以,最少需要3个矩阵。
后续我们要用q*k得到v的权重,然后进行一定缩放(除以根号d),再乘上v,就是第一个公式。
从数值上理解
wk我悟了,用引用的话行内公式不会乱
假设 a 1 = ( 1 , 1 ) a_1=(1,1) a1=(1,1), a 2 = ( 1 , 0 ) a_2=(1,0) a2=(1,0), W q = ( 1 1 0 1 ) W^q=\binom{1 \ \ \ 1}{0 \ \ \ 1} Wq=(0 11 1),那么根据以上的说法,我们可以计算出 q 1 q^1 q1、 q 2 q^2 q2。
q 1 = ( 1 , 2 ) ( 1 1 0 1 ) = ( 1 , 2 ) , q 2 = ( 1 , 0 ) ( 1 1 0 1 ) = ( 1 , 1 ) q^1=(1,2)\binom{1 \ \ \ 1}{0 \ \ \ 1}=(1,2),q^2=(1,0)\binom{1 \ \ \ 1}{0 \ \ \ 1}=(1,1) q1=(1,2)(0 11 1)=(1,2),q2=(1,0)(0 11 1)=(1,1)
此时可以并行化,就是把 q 1 q^1 q1和 q 2 q^2 q2在拼接起来,拼成 ( 1 1 1 0 ) \binom{1 \ \ \ 1}{1 \ \ \ 0} (1 01 1),在与 W q W^q Wq进行运算,结果不会发生改变
( q 1 q 2 ) = ( 1 1 1 0 ) ( 1 1 0 1 ) = ( 1 2 1 1 ) \binom{q^1}{q^2}=\binom{1 \ \ \ 1}{1 \ \ \ 0}\binom{1 \ \ \ 1}{0 \ \ \ 1}=\binom{1 \ \ \ 2}{1 \ \ \ 1} (q2q1)=(1 01 1)(0 11 1)=(1 11 2)
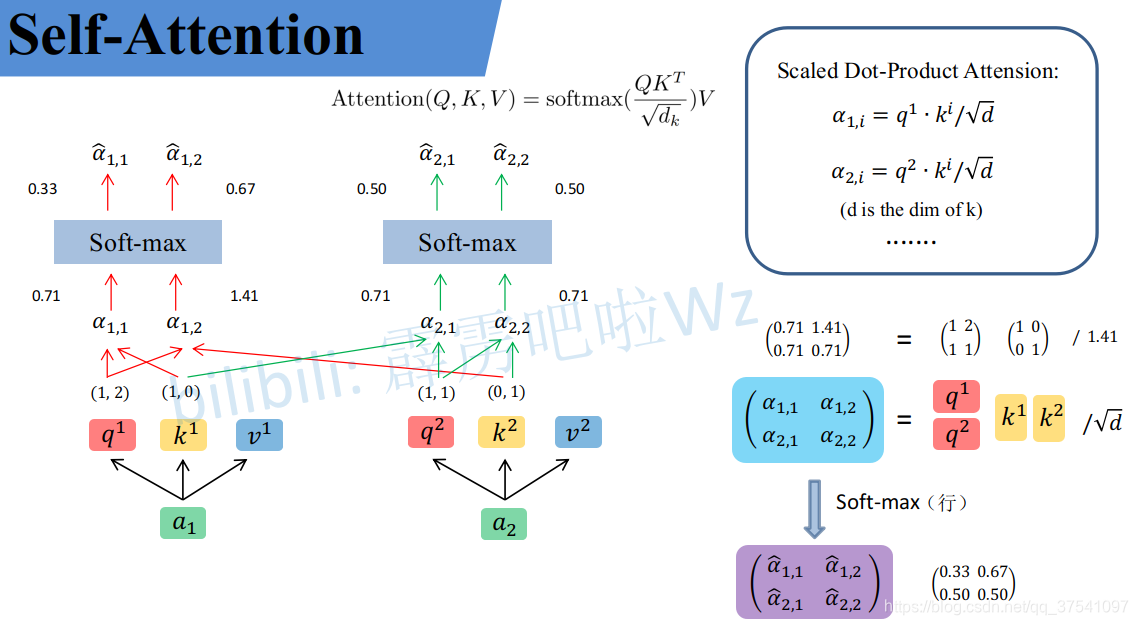
同理可以得到 ( k 1 k 2 ) \binom{k^1}{k^2} (k2k1)和 ( v 1 v 2 ) \binom{v^1}{v^2} (v2v1),求得的这些数值依次是q(Query),k(Key),v(Value)。接着先拿 q 1 q^1 q1和每个k进行match,点乘操作,接着除以 d \sqrt{d} d,得到对应的 α \alpha α,,其中 d d d代表向量 k i k^i ki的长度,此时等于2,除以 d \sqrt{d} d的原因在论文中的解释是“进行点乘后的数值很大,导致通过softmax后梯度变的很小,所以通过除以 d \sqrt{d} d来进行缩放,比如计算 α 1 , i \alpha_{1,i} α1,i:
α 1 , 1 = q 1 ⋅ k 1 d = 1 ∗ 1 + 2 ∗ 0 2 = 0.71 \alpha_{1,1}=\frac{{q^1} \cdot {k^1}}{\sqrt{d}}=\frac{1*1+2*0}{\sqrt2}=0.71 α1,1=dq1⋅k1=21∗1+2∗0=0.71α 1 , 2 = q 1 ⋅ k 2 d = 1 ∗ 0 + 2 ∗ 1 2 = 1.41 \alpha_{1,2}=\frac{{q^1} \cdot {k^2}}{\sqrt{d}}=\frac{1*0+2*1}{\sqrt2}=1.41 α1,2=dq1⋅k2=21∗0+2∗1=1.41
同理用 q 2 q^2 q2去匹配所有的k能得到 α 2 , i \alpha_{2,i} α2,i,统一写成矩阵乘法形式:
( α 1 , 1 α 1 , 2 α 2 , 1 α 2 , 2 ) = ( q 1 q 2 ) ( k 1 k 2 ) T d \binom{\alpha_{1,1} \ \ \ \alpha_{1,2}}{\alpha_{2,1} \ \ \ \alpha_{2,2}}=\frac{\binom{q^1}{q^2}{\binom{k^1}{k^2}}^T}{\sqrt{d}} (α2,1 α2,2α1,1 α1,2)=d(q2q1)(k2k1)T
然后对每一行即 ( α 1 , 1 , α 1 , 2 ) (\alpha_{1,1},\alpha_{1,2}) (α1,1,α1,2)分别进行softmax处理得到KaTeX parse error: Expected 'EOF', got '̂' at position 9: (\alpha ̲̂ _{1,1},\alpha …,这里的$\alpha ̂ 相当于计算得到针对每个 相当于计算得到针对每个 相当于计算得到针对每个v 的权重,到这我们就完成了第一个公式( 的权重,到这我们就完成了第一个公式( 的权重,到这我们就完成了第一个公式(Attention(Q,K,V) )中的 )中的 )中的softmax(\frac{QK^T}{\sqrt{d}})$部分
为啥这里又乱了。。

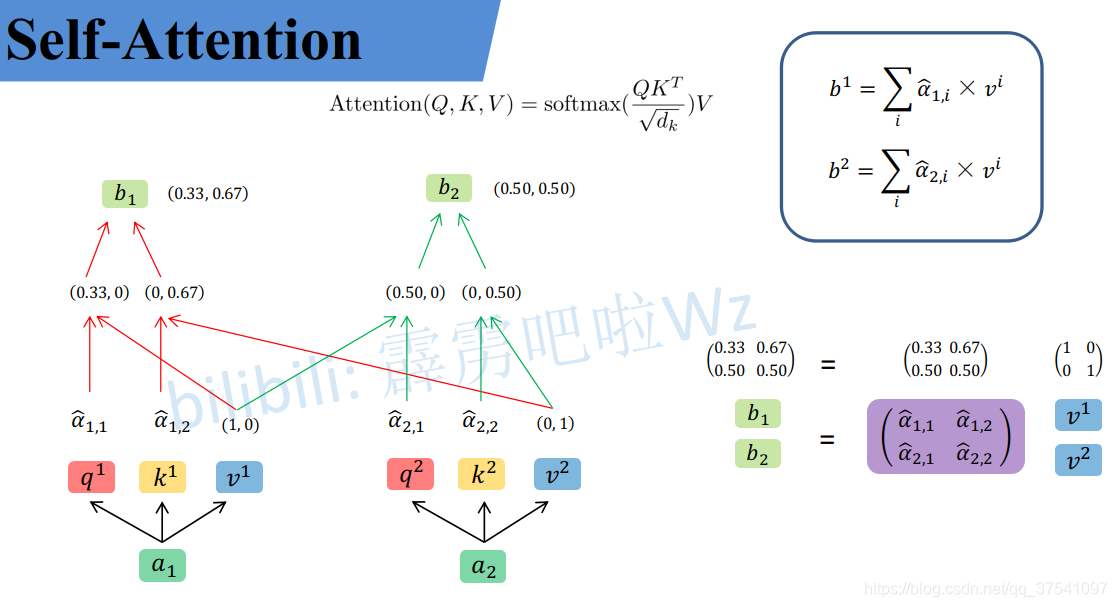
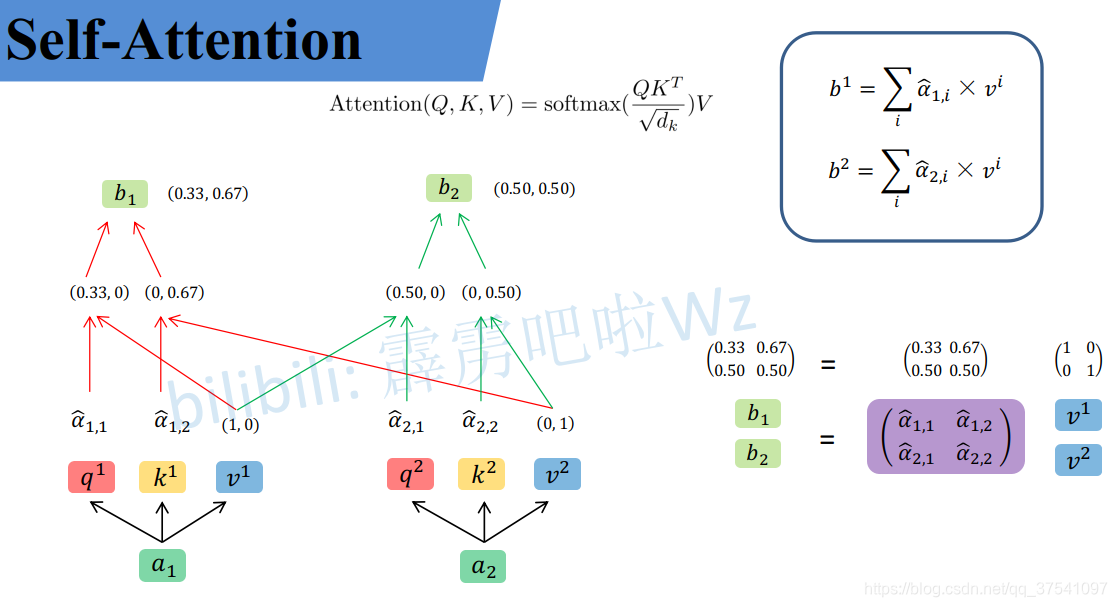
从维度上进行理解
我们假设载入的 x 1 x_1 x1经过Embedding后变为 a 1 a_1 a1维度为1X4, W q W^q Wq的维度为4X3,两者进行叉乘运算后就得到了维度为1X3的Query,k和v同理
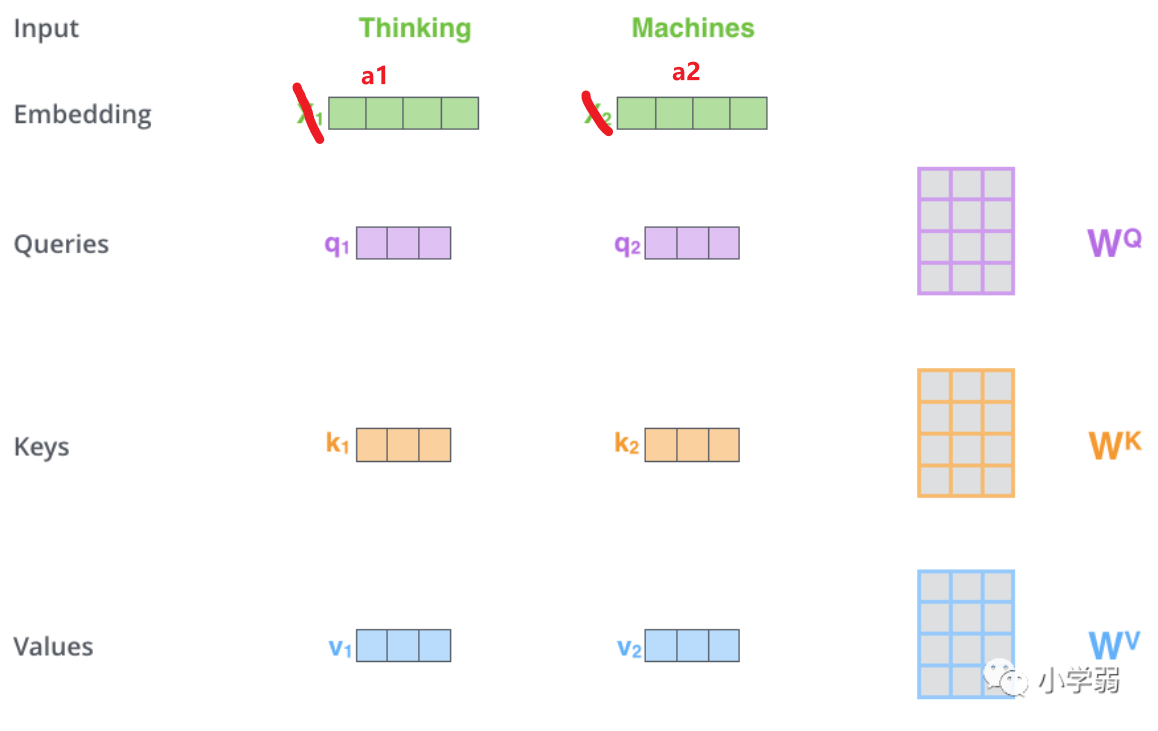
然后我们吧a1和a2并行起来
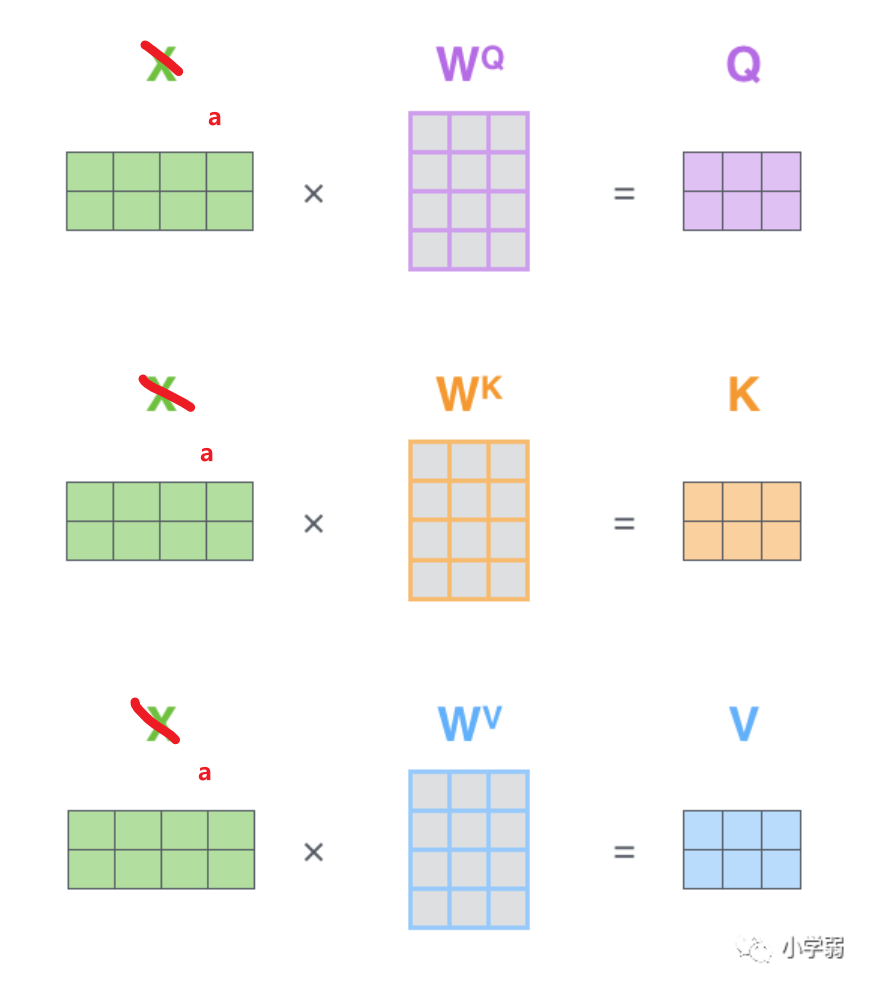
然后把公式中的式子也换成维度:
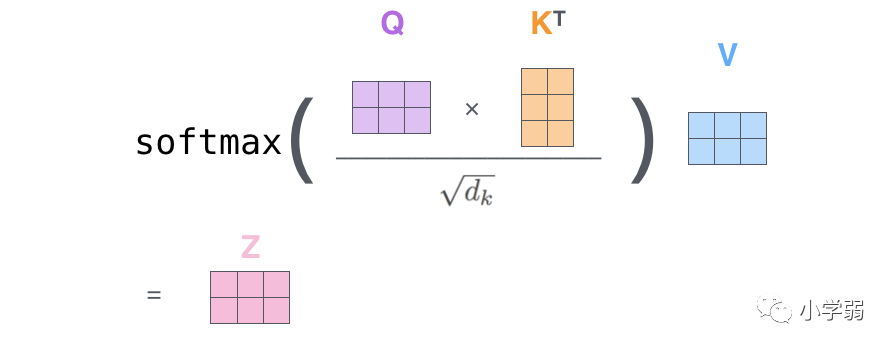
整个过程放在一张图上可以这么看:
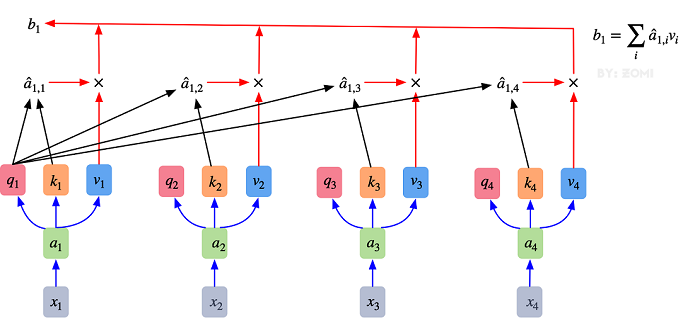
这里暂时不附代码,Multiple-Head Attention下篇记录。
打卡图片:
参考博客:
11.1 Vision Transformer(vit)网络详解_哔哩哔哩_bilibili
详解Transformer中Self-Attention以及Multi-Head Attention_transformer multi head-CSDN博客
Vision Transformer详解-CSDN博客
一文搞定自注意力机制(Self-Attention)-CSDN博客
以上图片均引用自以上大佬博客,如有侵权,请联系删除
相关文章:

240629_昇思学习打卡-Day11-Vision Transformer中的self-Attention
240629_昇思学习打卡-Day11-Transformer中的self-Attention 根据昇思课程顺序来看呢,今儿应该看Vision Transformer图像分类这里了,但是大概看了一下官方api,发现我还是太笨了,看不太明白。正巧昨天学SSD的时候不是参考了太阳花的…...

代码随想录-Day43
52. 携带研究材料(第七期模拟笔试) 小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等…...
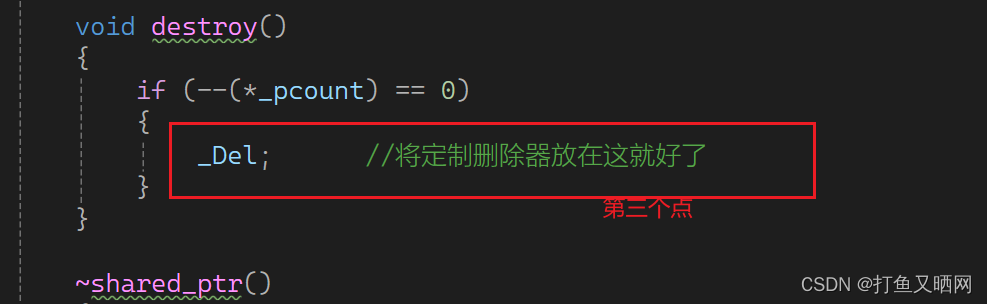
C++——探索智能指针的设计原理
前言: RAII是资源获得即初始化, 是一种利用对象生命周期来控制程序资源地手段。 智能指针是在对象构造时获取资源, 并且在对象的声明周期内控制资源, 最后在对象析构的时候释放资源。注意, 本篇文章参考——C 智能指针 - 全部用法…...

办公效率新高度:利用办公软件实现文件夹编号批量复制与移动,轻松管理文件
在数字化时代,我们的工作和生活都围绕着海量的数据和文件展开。然而,随着数据量的不断增加,如何高效地管理这些数字资产成为了摆在我们面前的一大难题。今天,我要向您介绍一种革命性的方法——利用办公软件实现文件夹编号批量复制…...
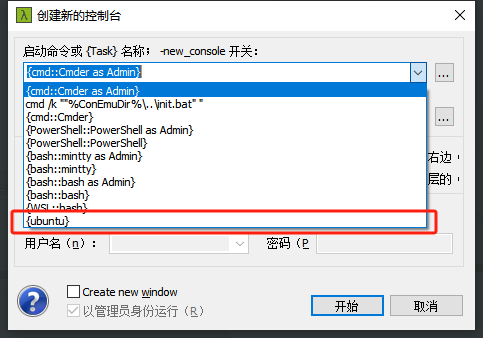
Windows kubectl终端日志聚合(wsl+ubuntu+cmder+kubetail)
Windows kubectl终端日志聚合 一、kubectl终端日志聚合二、windows安装ubuntu子系统1. 启用wsl支持2. 安装所选的 Linux 分发版 三、ubuntu安装kubetail四、配置cmder五、使用 一、kubectl终端日志聚合 k8s在实际部署时,一般都会采用多pod方式,这种情况下…...

【MySQL】数据库——事务
一.事务概念 事务是一种机制、一个操作序列,包含了一组数据库操作命令,并且把所有的命令作为一个整体一起向系统提交或撤销操作请求,即这一组数据库命令要么都执行,要么都不执行事务是一个不可分割的工作逻辑单元,在数…...
)
python代码缩进规范(2空格或4空格)
C、C、Java、C#、Rust、Go、JavaScript 等常见语言都是用"{“和”}"来标记一个块作用域的开始和结束,而Python 程序则是用缩进来表示块作用域的开始和结束: 作用域是编程语言里的一个重要的概念,特别是块作用域,编程语言…...

前后端分离的后台管理系统开发模板(带你从零开发一套自己的若依框架)上
前言: 目前,前后端分离开发已经成为当前web开发的主流。目前最流行的技术选型是前端vue3后端的spring boot3,本次。就基于这两个市面上主流的框架来开发出一套基本的后台管理系统的模板,以便于我们今后的开发。 前端使用vue3ele…...

【C++ | 委托构造函数】委托构造函数 详解 及 例子源码
😁博客主页😁:🚀https://blog.csdn.net/wkd_007🚀 🤑博客内容🤑:🍭嵌入式开发、Linux、C语言、C、数据结构、音视频🍭 🤣本文内容🤣&a…...

iCloud邮件全攻略:设置与使用终极指南
标题:iCloud邮件全攻略:设置与使用终极指南 摘要 iCloud邮件是Apple提供的一项邮件服务,允许用户在所有Apple设备上访问自己的邮件。本文将详细介绍如何在各种设备和邮件客户端上设置和使用iCloud邮件账户,确保用户能够充分利用…...

【计算机毕业设计】基于微信小程序的电子购物系统的设计与实现【源码+lw+部署文档】
包含论文源码的压缩包较大,请私信或者加我的绿色小软件获取 免责声明:资料部分来源于合法的互联网渠道收集和整理,部分自己学习积累成果,供大家学习参考与交流。收取的费用仅用于收集和整理资料耗费时间的酬劳。 本人尊重原创作者…...

CSS实现动画
CSS实现动画主要有三种方式:transition,transform,和animation1。以下是一些详细的逻辑,实例和注意事项: Transition:transition可以为一个元素在不同状态之间切换的时候定义不同的过渡效果。例如ÿ…...
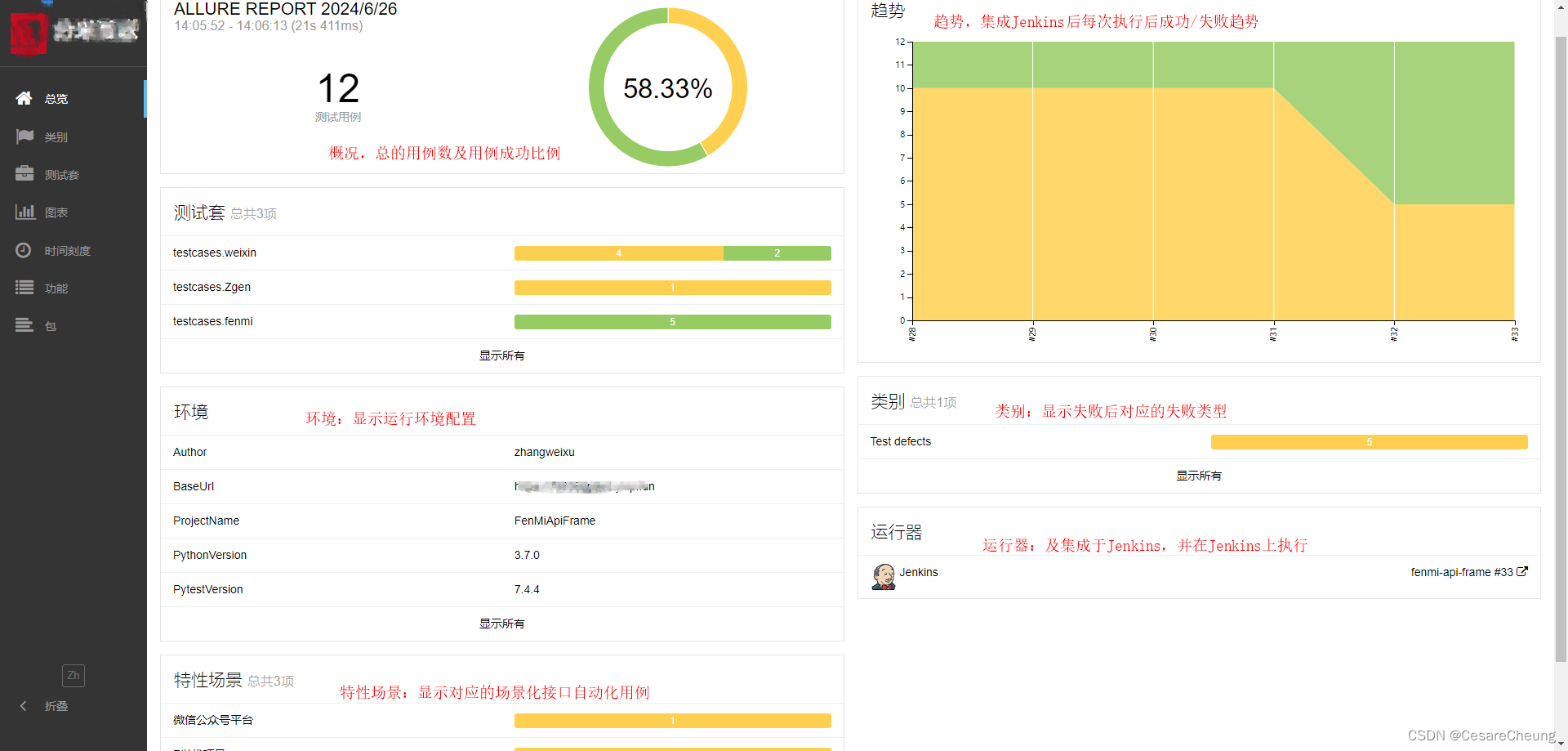
Python+Pytest+Allure+Yaml+Jenkins+GitLab接口自动化测试框架详解
PythonPytestAllureYaml接口自动化测试框架详解 编撰人:CesareCheung 更新时间:2024.06.20 一、技术栈 PythonPytestAllureYamlJenkinsGitLab 版本要求:Python3.7.0,Pytest7.4.4,Allure2.18.1,PyYaml6.0 二、环境配置 安装python3.7&…...
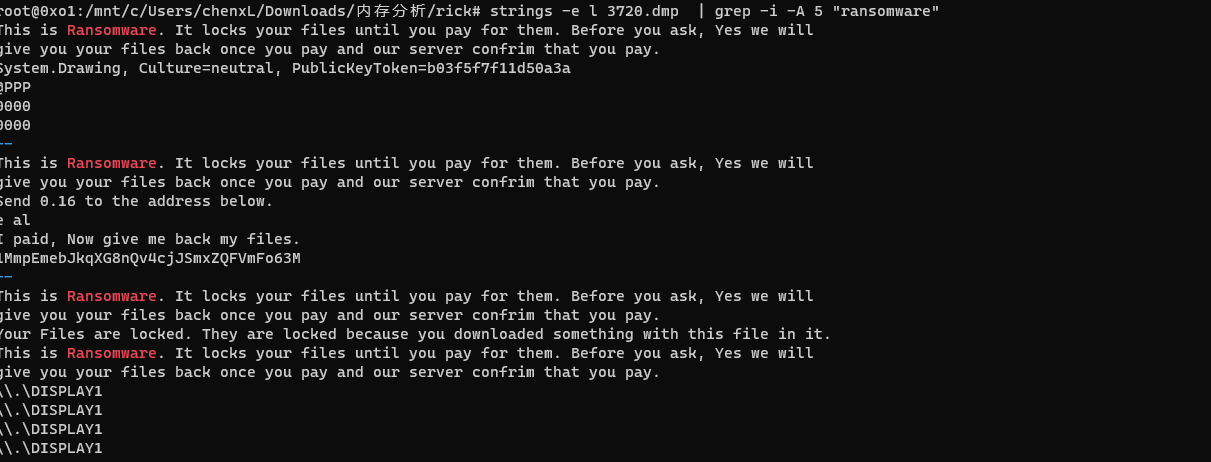
[OtterCTF 2018]Bit 4 Bit
我们已经发现这个恶意软件是一个勒索软件。查找攻击者的比特币地址。** 勒索软件总喜欢把勒索标志丢在显眼的地方,所以搜索桌面的记录 volatility.exe -f .\OtterCTF.vmem --profileWin7SP1x64 filescan | Select-String “Desktop” 0x000000007d660500 2 0 -W-r-…...
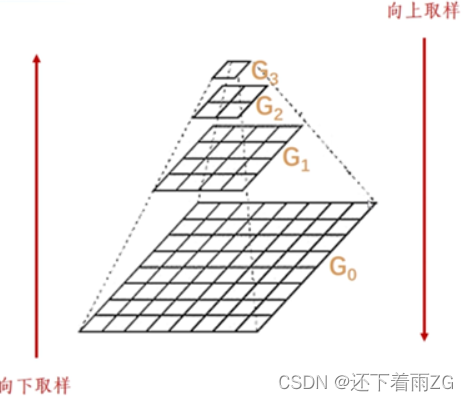
计算机视觉全系列实战教程 (十四):图像金字塔(高斯金字塔、拉普拉斯金字塔)
1.图像金字塔 (1)下采样 从G0 -> G1、G2、G3 step01:对图像Gi进行高斯核卷积操作(高斯滤波)step02:删除所有的偶数行和列 void cv::pyrDown(cv::Mat &imSrc, //输入图像cv::Mat &imDst, //下采样后的输出图像cv::Si…...

正确重写equals和hashcode方法
1. 重写的原因 如有个User对象如下: public class User {private String name;private Integer age; }如果不重写equals方法和hashcode方法,则: public static void main(String[] args) {User user1 new User("userA", 30);Us…...

数据质量管理-时效性管理
前情提要 根据GB/T 36344-2018《信息技术 数据质量评价指标》的标准文档,当前数据质量评价指标框架中包含6评价指标,在实际的数据治理过程中,存在一个关联性指标。7个指标中存在4个定性指标,3个定量指标; 定性指标&am…...

python 实例002 - 数据转换
题目: 有一组用例数据如下: cases [[case_id, case_title, url, data, excepted],[1, 用例1, www.baudi.com, 001, ok],[4, 用例4, www.baudi.com, 002, ok],[2, 用例2, www.baudi.com, 002, ok],[3, 用例3, www.baudi.com, 002, ok],[5, 用例5, www.ba…...

1.k8s:架构,组件,基础概念
目录 一、k8s了解 1.什么是k8s 2.为什么要k8s (1)部署方式演变 (2)k8s作用 (3)Mesos,Swarm,K8S三大平台对比 二、k8s架构、组件 1.k8s架构 2.k8s基础组件 3.k8s附加组件 …...
动态规划基础练习
我们需要先从数组较大的开始进行处理,每次考察上下左右的,比较当前存储的最大值和转移来的值,哪一个大一点 #define _CRT_SECURE_NO_WARNINGS #include<bits/stdc.h> using namespace std;int n, m; int a[105][105]; int addx[] { 0,…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
