力扣第一道困难题《3. 无重复字符的最长子串》,c++
目录
方法一:
方法二:
方法三:
方法四:
没有讲解,但给出了优秀题解
本题链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode)

话不多说,我们直接开始进行本题的思路解析;
首先我们看到这个题是肯定有一种暴力的硬解思路的,
方法一:
那就是将两个vector直接链接起来,然后再排序后,直接返回中间值,这个方法实现起来还是非常容易的,
代码如下:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2){size_t n = nums1.size();size_t m = nums2.size();if (m == 0){if (n % 2 == 0)return (nums1[n / 2 - 1] + nums1[n / 2]) / 2.0;elsereturn nums1[n / 2];}if (n == 0){if (m % 2 == 0)return (nums2[m / 2 - 1] + nums2[m / 2]) / 2.0;elsereturn nums2[m / 2];}size_t sum = m + n;int* nums = new int[m + n];int count = 0, i = 0, j = 0;while (count != sum){if (i == n){while (j != m)nums[count++] = nums2[j++];break;}if (j == m){while (i != n)nums[count++] = nums1[i++];break;}if (nums1[i] > nums2[j])nums[count++] = nums2[j++];elsenums[count++] = nums1[i++];}if (count % 2 == 0)return (nums[count / 2 - 1] + nums[count / 2]) / 2.0;elsereturn nums[count / 2];} };int main() {vector<int> s1;vector<int> s2;s1.push_back(1);s1.push_back(2);s2.push_back(3);s2.push_back(4);s2.push_back(5);s2.push_back(6);Solution s;cout << s.findMedianSortedArrays(s1, s2) << endl;return 0; }首先这个代码是可以编译成功的,
这里也有一个小技巧,如果这个代码是为0,那么证明编译时没有问题的,如果是非0,那么就是编译有问题,还需要修改代码。
但是会过来这个代码再力扣上是运行超时的,因为题目要求的时间复杂度是O(log (m+n))
但是我们的时间复杂度是O(m+n)
空间复杂度也是O(m+n)
方法二:
其实我们的方法一是我们真正的将两个vector真正的链接在了一起,但实际上我们这一步可以省略,我们只需要挨个比较得到第k(假设中位数为第k位)个大的数是多少,那么其实就得到了中位数是多少。其实这一题方便了一点,题目给的数组是已有序的,所以我们挨个比较就行
开始我们写一个循环,这个循环我们的目的就是找到中位数所对应的下标是多少,如果找到了,那么就返回他的下标值,还没找到,那么就继续。但是这样来说,对偶数和奇数的分类会很麻烦。当其中一个数组遍历完后,还要分好几种情况进行另类判断另一个数组,这样想起来都麻烦。
然而要进行优化,那么我们就需要找到要进行优化的部分,那么就是考虑对偶与奇的情况不分开讨论,进行合并考虑,对于此情况我们可以在另定义两个变量left与right分别保存左操作数与右操作数。
假设合并的数组长度为len,那么无论对应偶还是奇,我们只需要遍历前 len/2+1 个数就可以(如果是偶数,我们需要知道第 len/2和 len/2+1 个数,也是需要遍历 len/2+1 次。所以遍历的话,奇数和偶数都是 len/2+1 次。)
返回的left与right我们要做到如果是奇,那么只需要right,如果是偶,因为left不等于right,所以返回两个数的平均数;所以我们在for循环里应该保证依次循环过后left与right差一个位,所以我们要先在循环开始将right的值赋给left,后进行调整right。
然后写出大致框架:
如果nums1[i]<nums2[i],那么就将nums1[i]赋值给right,反之nums2[i];
我们在调整right的时候首先要考虑的就是nums是否越界,所以我需要先判断是否越界,同理考虑了nums1也需要考虑nums2;
所以填充完代码如下:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size();int n = nums2.size();int len = m + n;int left = -1, right = -1;int aStart = 0, bStart = 0;for (int i = 0; i <= len / 2; i++) {left = right;//调整rightif (aStart < m && (bStart >= n || nums1[aStart] < nums2[bStart])) {right = nums1[aStart++];}else {right = nums2[bStart++];}}if ((len % 2) == 0)return (left + right) / 2.0;elsereturn right;} }; int main() {vector<int> s1;vector<int> s2;s1.push_back(1);s1.push_back(2);s2.push_back(3);s2.push_back(4);s2.push_back(5);s2.push_back(6);Solution s;cout << s.findMedianSortedArrays(s1, s2) << endl;return 0; }
运行起来是正确的,但依然在力扣上是不行的,还是运行超时;
时间复杂度是:遍历了m+n/2+1个数,但时间复杂度还是O(m+n);
方法三:
我第一眼看到这个题的时候,首先想到的就是二分查找,然后就想到了分别对两个数组进行二分,但是如果nums2全都大于num1那么这样就不行,然后我在看了别人的题解后然后理解了理解,就大为震撼,妙,但是题解是java的然后我自己又写了写修改了好几次终于写出来了。
方法二中,我们一次遍历就相当于去掉不可能是中位数的一个值,也就是一个一个排除。由于数列是有序的,其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数,我们可以每次循环排除掉 k/2 个数。方法三其实与方法二同理,也是主要找到第k个数是多少。
下面我们看一个例子


此时3=3
然后我们需要将两个数组的第 k/2 个数进行比较 ,然后将小的那个数组前k/2个数舍弃,对于方便处理,我们设定如果两个数相等,目前我们先优先删除第二个数组删除;(后面代码是是先有限舍弃第一个数组,这里是为了避开特殊情况)
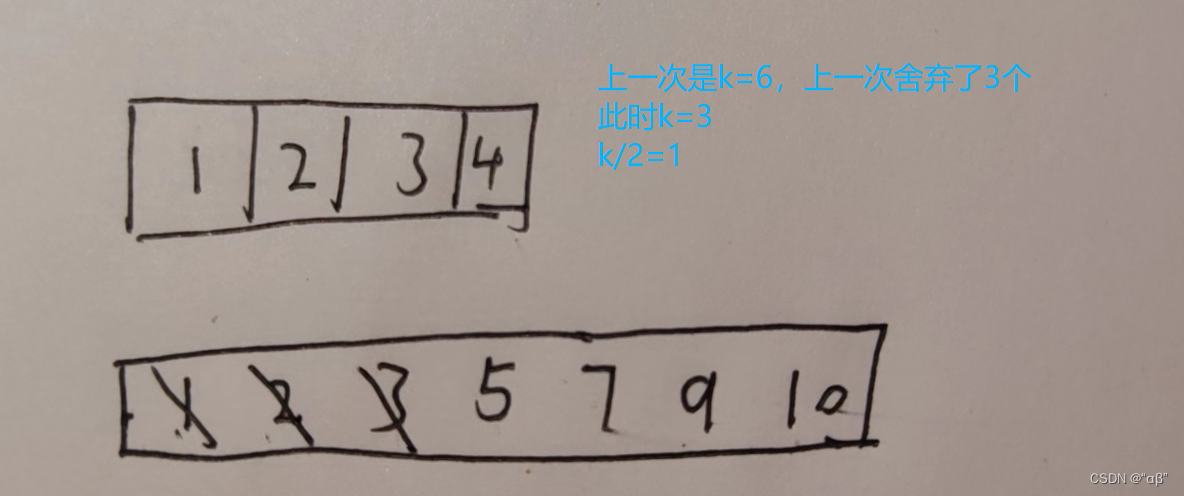

此时1<5
这次舍弃num1 的 k/2 个数;


此时2<5
同理,继续舍弃nums1,舍弃 k/2 个数
 这时候3<5;这时候3就为第6大的数,就是中位数。
这时候3<5;这时候3就为第6大的数,就是中位数。
这个方法是不是很妙呢?
然后我们就刷刷的写,然后突然就有一个案例不通过,那就是
如果按照上面的方法进行按照步骤进行梳理,那么就会发现第一步的时候就会卡住,因为第一步我么要进行舍弃的数的个数就已经超出了nums1的长度,直接会越界,那么这时候我们就需要进行特殊处理,如果舍弃个数大于剩余长度,那么就舍弃剩余长度。
思路全部梳理完后,如果对递归熟悉的话,那么就完全可以写出来,思路难想,但是代码实现还是比较简单的。(特殊案例我也进行处理了,后面会进行特别分析)
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();int left = (n + m + 1) / 2;int right = (n + m + 2) / 2;return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;}int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k){//舍弃k/2个//结束条件k==1int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);//还存在一种情况,就是k不为1的情况下,但len1已经等于0if (len1 == 0) return nums2[start2 + k - 1]; if (k == 1)return min(nums1[start1], nums2[start2]);int i = start1 + min(len1, k / 2) - 1;int j = start2 + min(len2, k / 2) - 1;if (nums1[i] > nums2[j]){return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));}else{return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}}
};到此我们就出来了第一种在力扣上通过的代码;
然后进行特别分析
1:
这一步也是跟方法二同样的找到求中位数的操作数第left是第几个,right是第几个;与之不同的就是奇的情况下left=right,偶的情况下left+1=right;
2:
此案例对应的也就是
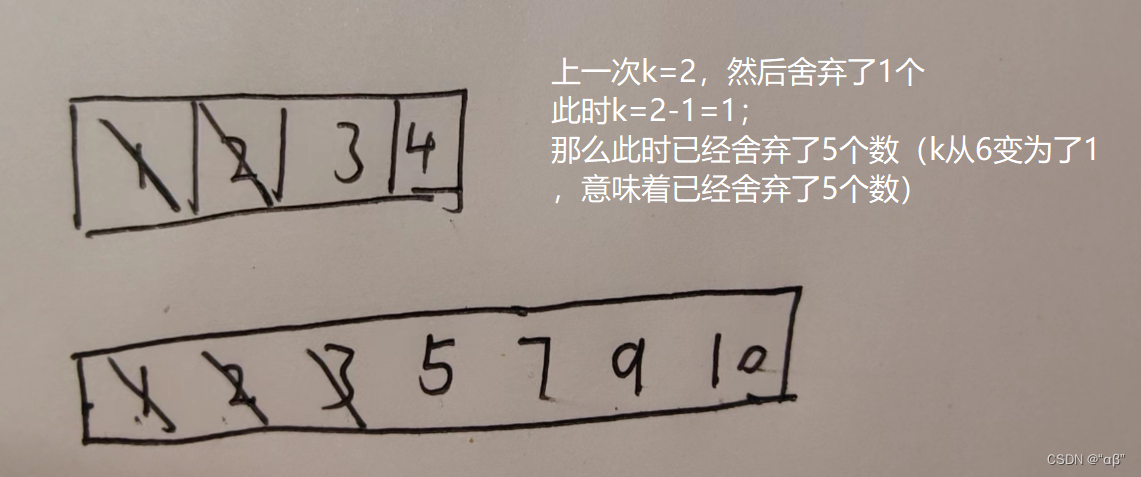
在求right的时候k=7;先舍弃k/2=3个
此时k=4;
然后再舍弃的话num1已经没有了但是k=4-2=2;还不为1;如果返回的还要再舍弃的话,就会报错越界;
所以要加特殊情况处理
3: 
这一步也是为了对应2,方便,如果没有这个,那么就有可能len2先空的情况,所以这一步避免了分类讨论;
最后再展示一边代码:
class Solution { public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size();int m = nums2.size();int left = (n + m + 1) / 2;int right = (n + m + 2) / 2;return (getKth(nums1, 0, n - 1, nums2, 0, m - 1, left) + getKth(nums1, 0, n - 1, nums2, 0, m - 1, right)) * 0.5;}int getKth(vector<int>& nums1, int start1, int end1, vector<int>& nums2, int start2, int end2, int k){//舍弃k/2个//结束条件k==1int len1 = end1 - start1 + 1;int len2 = end2 - start2 + 1;//让 len1 的长度小于 len2,这样就能保证如果有数组空了,一定是 len1 if (len1 > len2) return getKth(nums2, start2, end2, nums1, start1, end1, k);//还存在一种情况,就是k不为1的情况下,但len1已经等于0if (len1 == 0){return nums2[start2 + k - 1];}if (k == 1)return min(nums1[start1], nums2[start2]);int i = start1 + min(len1, k / 2) - 1;int j = start2 + min(len2, k / 2) - 1;if (nums1[i] > nums2[j]){return getKth(nums1, start1, end1, nums2, j + 1, end2, k - (j - start2 + 1));}else{return getKth(nums1, i + 1, end1, nums2, start2, end2, k - (i - start1 + 1));}} };运行成功
时间复杂度是
O(log (m+n))。符合要求
方法四:
但是这个方法三还是效率不是很高, 
其实还有一种更牛的方法,但本人看了看看不明白,运用到了统计学;本人还没有学统计学,能看明白一点,但是还是看清楚;
我看了题解有两种一个数官方一个是别的作者大佬写的;本人推荐大佬,官方直接给了题目解释,没有给知识补充;
4. 寻找两个正序数组的中位数 - 力扣(LeetCode)
为了方便这里给出了全部官方截图:

最后这个题就已经完全讲解完了,第一次完全写完力扣困难题,总的来说是很难,但不至于一点思路也没有,而且写的过程中思考是很多的,还是比简单题写起来吃力。有能力还是多写困难题;
相关文章:

力扣第一道困难题《3. 无重复字符的最长子串》,c++
目录 方法一: 方法二: 方法三: 方法四: 没有讲解,但给出了优秀题解 本题链接:4. 寻找两个正序数组的中位数 - 力扣(LeetCode) 话不多说,我们直接开始进行本题的思路解…...

【ai】tx2 nx :ubuntu查找NvInfer.h 路径及哪个包、查找符号
在Ubuntu系统中,你可以使用多种方法来查找某个头文件的路径。这里有几种常用的方法: 使用find命令: find命令是一个非常强大的工具,可以在文件系统中搜索匹配特定条件的文件。例如,如果你想查找名为stdio.h的头文件,可以使用以下命令:bash 复制代码 sudo find / -name …...

C++ 运算符的优先级和结合性表
优先级和结合性表 优先级运算符描述结合性1::作用域解析运算符左到右2() [] . -> --后缀运算符左到右3 -- - ! ~ * & sizeof new delete typeid一元运算符右到左4* / %乘除取模左到右5 -加法和减法左到右6<< >>左移和右移左到右7< < > >关系…...

MySQL中SQL语句的执行过程详解
1. 客户端连接和请求 客户端连接 在MySQL中,客户端连接和请求过程是执行SQL语句的第一步。该步骤主要涉及客户端如何连接到MySQL服务器,以及如何维护和管理客户端与服务器之间的会话。 客户端连接: 连接器(Connector)…...
文心一言4.0免费使用
领取&安装链接:Baidu Comate 领取季卡 视频教程:免费使用文心一言4.0大模型_哔哩哔哩_bilibili 有图有真相 原理:百度comate使用文心一言最新的4.0模型。百度comate目前免费使用,可以借助comate达到免费使用4.0模型目的。 …...
Mongodb安装与配置
Mongodb的下载 这里下载的是MongoDB 7.0.11版本的 首先进入官网:https://www.mongodb.com/ 点击完上面两步后,加载来到该页面,选择自己的版本、系统,是压缩包(zip)还是安装包(msi)。 下载好之后能,来到安装包哪里&a…...

Java校园跑腿小程序校园代买帮忙外卖源码社区外卖源码
🔥校园跑腿与外卖源码揭秘🔥 🚀 引言:为何需要校园跑腿与外卖源码? 在快节奏的校园生活里,学生们对于便捷、高效的服务需求日益增长。校园跑腿和外卖服务成为了解决这一需求的热门选择。然而,…...

MySQL高级-MVCC-基本概念(当前读、快照读)
文章目录 1、MVCC基本概念1.1、当前读1.1.1、创建表 stu1.1.2、测试 1.2、快照读 1、MVCC基本概念 全称Multi-Version Concurrency Control,多版本并发控制。指维护一个数据的多个版本,使得读写操作没有冲突,快照读为MySQL实现MVCC提供了一个…...
kubernetes给指定用户分配调用k8s的api权限
文章目录 概要利用RBAC添加角色权限使用shell命令创建角色权限使用配置文件创建角色权限 调用k8s的api获取k8s账户的token 小结 概要 使用kubernetes部署项目时,有些特殊场景,我们需要在自己创建的pod里面调用k8s的api来管理k8s,但是需要使用…...

无人机的弱点和限制
1.电池和续航能力: 续航时间短:大多数无人机依赖锂电池供电,续航时间通常在30分钟至1小时之间,限制了其长时间任务的执行能力。 能量密度低:现有电池技术的能量密度无法满足长时间飞行需求,需要突破性的发…...

ElementUI的基本搭建
目录 1,首先在控制终端中输入下面代码:npm i element-ui -S 安装element UI 2,构架登录页面,login.vue编辑 3,在官网获取对应所需的代码直接复制粘贴到对应位置 4,在继续完善,从官网添加…...
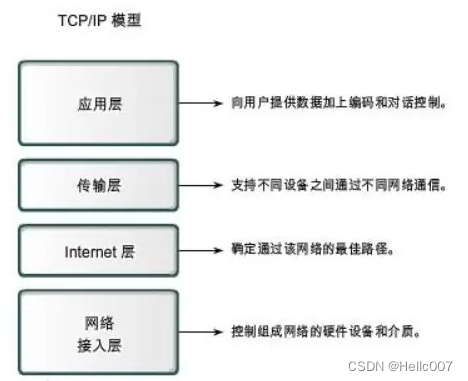
Modbus TCP与TCP/IP协议间的差异与应用场景
Modbus TCP概述 Modbus协议简介 Modbus是一种专为工业自动化系统设计的通信协议,采用主从模式,即一个主设备(通常是计算机或可编程逻辑控制器)与多个从设备(如传感器、执行器等)进行通信。Modbus协议具有…...
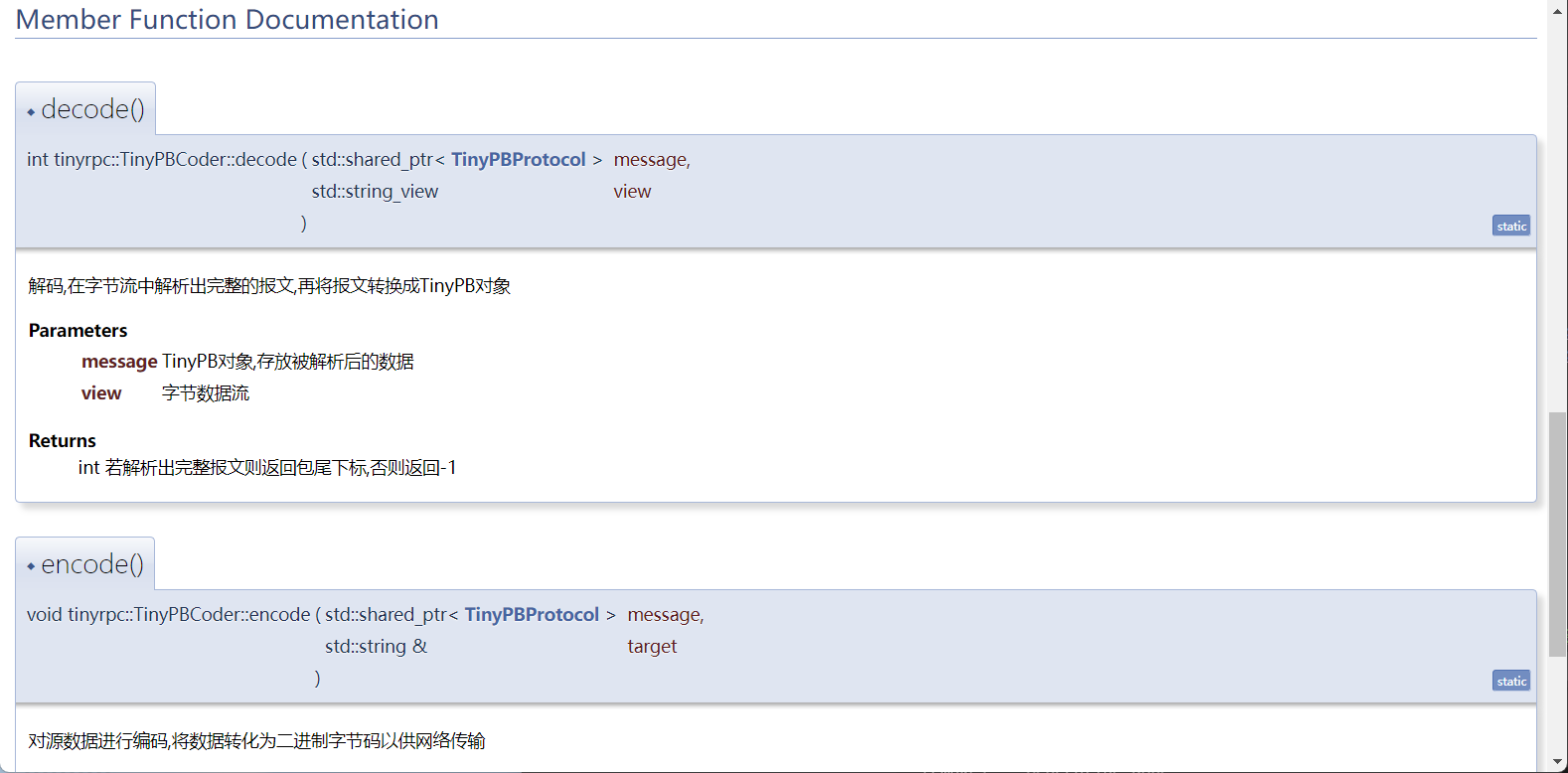
Linux Doxygen快速生成文档
此前写过一篇编写Doxygen格式的注释以用于生成文档,点击以查阅, Doxygen常用语法与字段记录,但是当时用的windows桌面版的doxygen,最近使用ubuntu编写代码想直接使用doxygen生成,故写下此博客 Doxygen Doxygen是一个用于生成软件文档的工具,它可以从代码中提取注释…...

MobPush REST API的推送 API之批量推送
调用验证 详情参见 REST API 概述的 鉴权方式 说明。 频率控制 详情参见推送限制策略的 接口限制 说明。 调用地址 POST http://api.push.mob.com/v3/push/createMulti 推送对象 以 JSON 格式表达,表示一条推送相关的所有信息 字段类型必须说明pushWorkobje…...

Arthas快速入门
简介 Arthas 是一款线上监控诊断产品,通过全局视角实时查看应用 load、内存、gc、线程的状态信息,并能在不修改应用代码的情况下,对业务问题进行诊断,包括查看方法调用的出入参、异常,监测方法执行耗时,类…...
python系列30:各种爬虫技术总结
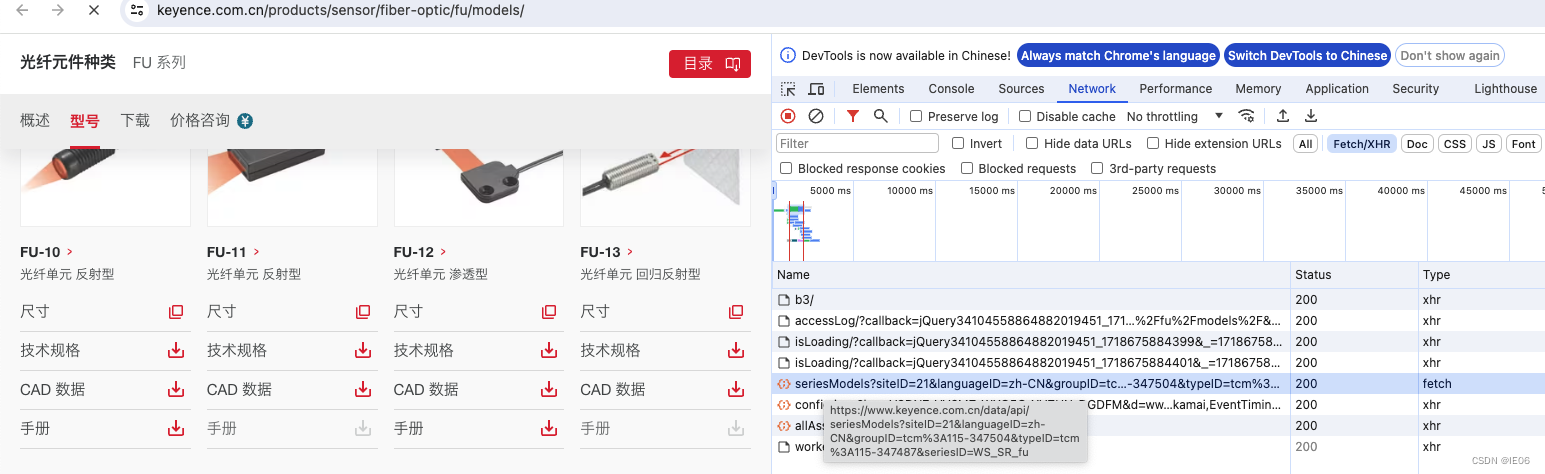
1. 使用requests获取网页内容 以巴鲁夫产品为例,可以用get请求获取内容: https://www.balluff.com.cn/zh-cn/products/BES02YF 对应的网页为: 使用简单方法进行解析即可 import requests r BES02YF res requests.get("https://www.…...

PHP和phpSpider:如何应对反爬虫机制的封锁?
php和phpspider:如何应对反爬虫机制的封锁? 引言: 随着互联网的快速发展,对于大数据的需求也越来越大。爬虫作为一种抓取数据的工具,可以自动化地从网页中提取所需的信息。然而,由于爬虫的存在,…...
学生宿舍管理系统
摘 要 随着高校规模的不断扩大和学生人数的增加,学生宿舍管理成为高校日常管理工作中的重要组成部分。传统的学生宿舍管理方式往往依赖于纸质记录和人工管理,这种方式不仅效率低下,而且容易出错,无法满足现代高校管理的需求。因此…...

一分钟彻底掌握Java迭代器Iterator
Iterator Iterator 是 Java 的 java.util 包中的一个接口 iterator() 是 Java 集合框架中的一个方法,它返回一个 Iterator 对象,该对象可以用来遍历集合中的元素。 Iterator确实是一个接口,你不能直接实例化一个接口。但是,你可以…...

第三十七篇——麦克斯韦的妖:为什么要保持系统的开放性?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 如果没有详细的学习这篇文章,我觉得我就是被麦克斯韦妖摆弄的…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...


