ForkJoin
线程数超过CPU核心数是没有任何意义的【因为要使用CPU密集型运算】
Fork/Join:线程池的实现,体现是分治思想,适用于能够进行任务拆分的 CPU 密集型运算,用于并行计算
任务拆分:将一个大任务拆分为算法上相同的小任务,直至不能拆分可以直接求解。跟递归相关的一些计算,如归并排序、斐波那契数列都可以用分治思想进行求解
-
Fork/Join 在分治的基础上加入了多线程,把每个任务的分解和合并交给不同的线程来完成,提升了运算效率
-
ForkJoin 使用 ForkJoinPool 来启动,是一个特殊的线程池,默认会创建与 CPU 核心数大小相同的线程池
-
任务有返回值继承 RecursiveTask,没有返回值继承 RecursiveAction【特殊:不能用Runnable或者Callable了】
public static void main(String[] args) {ForkJoinPool pool = new ForkJoinPool(4);System.out.println(pool.invoke(new MyTask(5)));//拆分 5 + MyTask(4) --> 4 + MyTask(3) -->}// 1~ n 之间整数的和class MyTask extends RecursiveTask<Integer> {private int n;public MyTask(int n) {this.n = n;}@Overridepublic String toString() {return "MyTask{" + "n=" + n + '}';}@Overrideprotected Integer compute() {// 如果 n 已经为 1,可以求得结果了if (n == 1) {return n;}// 将任务进行拆分(fork)MyTask t1 = new MyTask(n - 1);t1.fork(); //执行计算// 合并(join)结果int result = n + t1.join(); //获取上面fork的执行结果return result;}}继续拆分优化:二分法
class AddTask extends RecursiveTask<Integer> {int begin;int end;public AddTask(int begin, int end) {this.begin = begin;this.end = end;}@Overridepublic String toString() {return "{" + begin + "," + end + '}';}@Overrideprotected Integer compute() {// 5, 5if (begin == end) {return begin;}// 4, 5 防止多余的拆分 提高效率if (end - begin == 1) {return end + begin;}// 1 5int mid = (end + begin) / 2; // 3AddTask t1 = new AddTask(begin, mid); // 1,3t1.fork();AddTask t2 = new AddTask(mid + 1, end); // 4,5t2.fork();int result = t1.join() + t2.join();return result;}}ForkJoinPool 实现了工作窃取算法来提高 CPU 的利用率:
-
每个线程都维护了一个双端队列,用来存储需要执行的任务
-
工作窃取算法允许空闲的线程从其它线程的双端队列中窃取一个任务来执行
-
窃取的必须是最晚的任务,避免和队列所属线程发生竞争,但是队列中只有一个任务时还是会发生竞争
难在如何拆分,后面JDK8就封装到stream的api了,并行流
相关文章:

ForkJoin
线程数超过CPU核心数是没有任何意义的【因为要使用CPU密集型运算】 Fork/Join:线程池的实现,体现是分治思想,适用于能够进行任务拆分的 CPU 密集型运算,用于并行计算 任务拆分:将一个大任务拆分为算法上相同的小任务…...
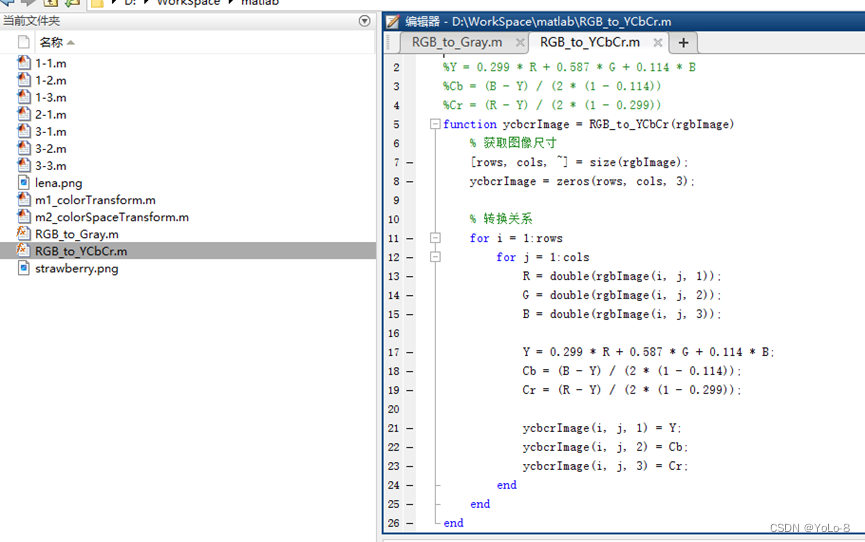
实验2 色彩模式转换
1. 实验目的 ①了解常用的色彩模式,理解色彩模式转换原理; ②掌握Photoshop中常用的颜色管理工具和色彩模式转换方法; ③掌握使用Matlab/PythonOpenCV编程实现色彩模式转换的方法。 2. 实验内容 ①使用Photoshop中的颜色管理工具ÿ…...
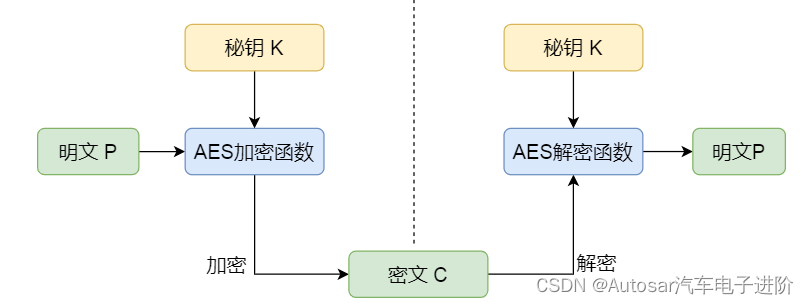
AES加密算法及AES-CMAC原理白话版系统解析
本文框架 前言1. AES加密理论1.1 不同AES算法区别1.2 加密过程介绍1.2.1 加密模式和填充方案选择1.2.2 密钥扩展1.2.3分组处理1.2.4多轮加密1.2.4.1字节替换1.2.4.2行移位1.2.4.3列混淆1.2.4.4轮密钥加1.3 加密模式1.3.1ECB模式1.3.2CBC模式1.3.3CTR模式1.3.4CFB模式1.3.5 OFB模…...

24年hvv前夕,微步也要收费了,情报共享会在今年结束么?
一个人走的很快,但一群人才能走的更远。吉祥同学学安全https://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247483727&idx1&sndb05d8c1115a4539716eddd9fde4e5c9&scene21#wechat_redirect这个星球🔗里面已经沉淀了: 《Ja…...

【地理库 Turf.js】
非常全面的地理库 , 这里枚举一些比较常用,重点的功能, 重点功能 提供地理相关的类:包括点,线,面等类。 测量功能:点到线段的距离,点和线的关系等。 判断功能: 点是否在…...
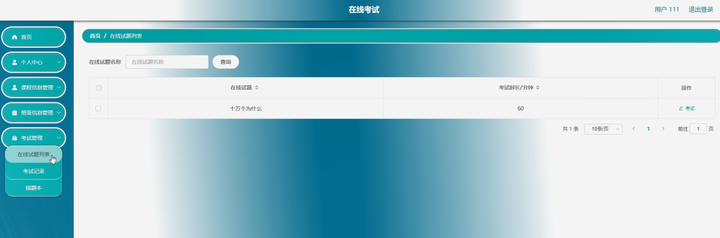
springboot在线考试 LW +PPT+源码+讲解
第三章 系统分析 3.1 可行性分析 一个完整的系统,可行性分析是必须要有的,因为他关系到系统生存问题,对开发的意义进行分析,能否通过本系统来补充线下在线考试管理模式中的缺限,去解决其中的不足等,通过对…...

JDBC中的事务及其ACID特性
在JDBC(Java Database Connectivity)中,事务(Transaction)是指作为单个逻辑工作单元执行的一系列操作。这些操作要么全部执行,要么全部不执行,从而确保数据库的完整性和一致性。事务是现代数据库…...

Python | Leetcode Python题解之第204题计数质数
题目: 题解: MX5000000 is_prime [1] * MX is_prime[0]is_prime[1]0 for i in range(2, MX):if is_prime[i]:for j in range(i * i, MX, i):#循环每次增加iis_prime[j] 0 class Solution:def countPrimes(self, n: int) -> int:return sum(is_prim…...
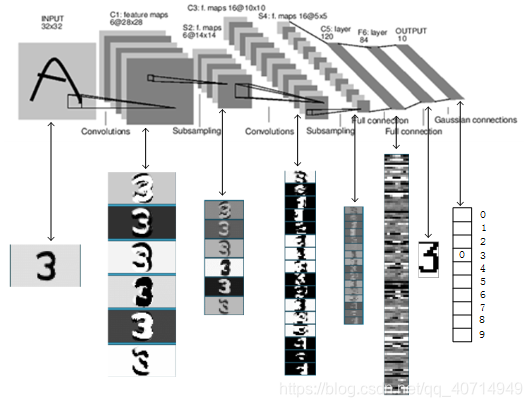
【课程总结】Day10:卷积网络的基本组件
前言 由于接下来的课程内容将围绕计算机视觉展开,其中接触最多的内容是卷积、卷积神经网络等…因此,本篇内容将从卷积入手,梳理理解:卷积的意义、卷积在图像处理中的作用以及卷积神经网络的概念,最后利用pytorch搭建一…...

ModuleNotFoundError: No module named ‘_sysconfigdata_x86_64_conda_linux_gnu‘
ModuleNotFoundError: No module named _sysconfigdata_x86_64_conda_linux_gnu 1.软件环境⚙️2.问题描述🔍3.解决方法🐡4.结果预览🤔 1.软件环境⚙️ Ubuntu 20.04 Python 3.7.0 2.问题描述🔍 今天发现更新conda之后࿰…...
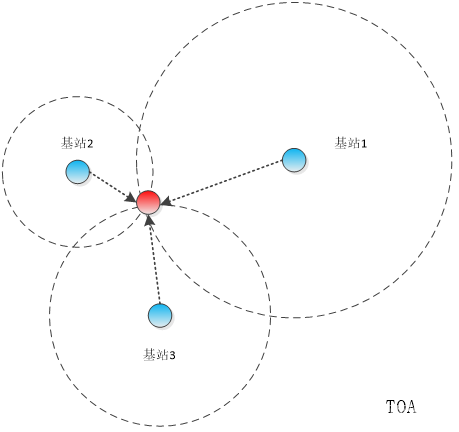
【物联网】室内定位技术及定位方式简介
目录 一、概述 二、常用的室内定位技术 2.1 WIFI技术 2.2 UWB超宽带 2.3 蓝牙BLE 2.4 ZigBee技术 2.5 RFID技术 三、常用的室内定位方式 3.1 信号到达时间 3.2 信号到达时间差 3.3 信号到达角 3.4 接收信号强度 一、概述 GPS是目前应用最广泛的定位技术࿰…...
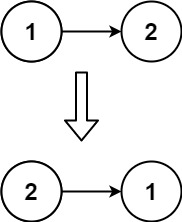
Leetcode[反转链表]
LCR 024. 反转链表 给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2: 输入:head [1,2] 输出:[2,1]示…...

【差分数组】个人练习-Leetcode-2249. Count Lattice Points Inside a Circle
题目链接:https://leetcode.cn/problems/count-lattice-points-inside-a-circle/description/ 题目大意:给出一系列圆的圆心坐标和半径,求在这些圆内部(边缘也算)的格点的数量。 思路:简单的思路就是暴力…...

【JavaEE】Cookie和Session详解
一.Cookie 首先我们知道HTTP协议本身是’‘无状态’‘的, 这里的’‘无状态’指的是:默认情况下HTTP协议的客户端和服务器之间的这次通信,和下次通信之间没有直接的联系. 但是在实际的开发过程之中, 我们很多时候是需要知道请求之间的关联关系的. 例如登陆网站成功后,第二次访…...

uniapp canvas vue3 ts实例
<template><view><canvas canvas-idcanvas-test class"canvas-test"></canvas></view> </template><script setup lang"ts">//封装的jsimport libs from /libs;//重点引入的import type { ComponentInternalIns…...

网络构建关键技术_3.SDN技术
SDN网络在控制平面和转发平面分别采用了不同技术,以满足SDN网络控件的全局性和灵活性,业务转发的高效性及高性价比要求。主要关键技术包括:控制平面技术、数据平面技术和转发规则一致性更新技术等。 1.控制平面技术 控制器是控制平面核心部件…...
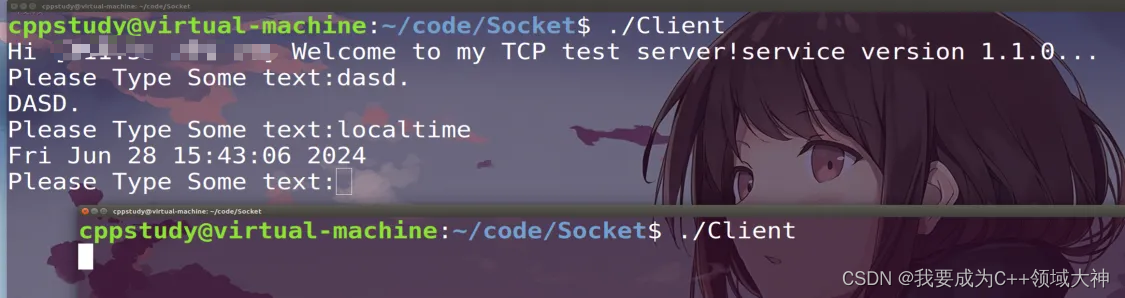
【高性能服务器】单进程服务器
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 单进程服务器 …...
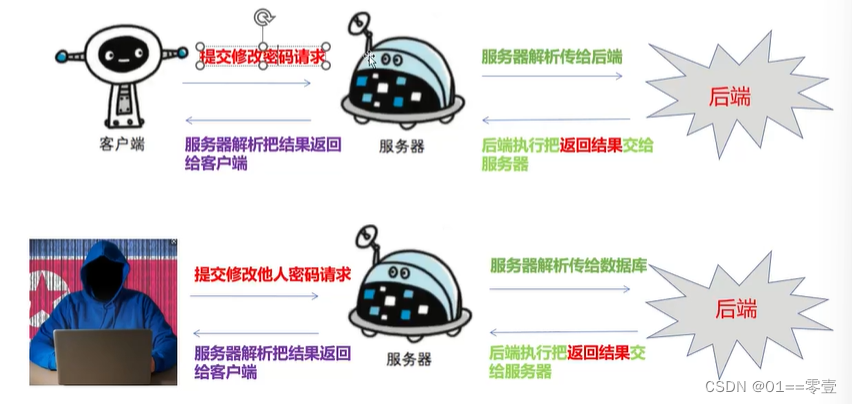
任意密码重置漏洞
文章目录 1. 任意密码重置漏洞原理2. 任意密码重置漏洞产生原因3. 任意密码重置漏洞场景3.1 验证码爆破3.2 验证凭证回传3.3 验证凭证未绑是用户3.4 跳过验证步骤3.5 凭证可预测3.6 同时向多个账户发送凭证 4. 任意密码重置经典案例4.1 中国人寿某重要系统任意账户密码重置4.2 …...

synchronized关键字和ReentrantLock在不同jdk版本中性能哪个高?该怎么选择呢?
synchronized关键字和ReentrantLock在不同JDK版本中的性能差异经历了显著的变化。早期,在JDK 1.5及以前的版本中,ReentrantLock通常提供了更好的性能,主要是因为synchronized关键字的实现较为简单,没有太多的优化,导致…...
【旭日x3派】部署官方yolov5全流程
地平线旭日x3派部署yolov5--全流程 前言一、深度学习环境安装二、安装docker三、部署3.1、安装工具链镜像3.2、配置天工开物OpenExplorer工具包3.3、创建深度学习虚拟空间,安装依赖:3.4、下载yolov5项目源码并运行3.5、pytorch的pt模型文件转onnx3.6、最…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...
