二叉树第二期:堆的实现与应用
若对树与二叉树的相关概念,不太熟悉的同学,可移置上一期博客
链接:二叉树第一期:树与二叉树的概念-CSDN博客
本博客目标:对二叉树的顺序结构,进行深入且具体的讲解,同时学习二叉树顺序结构的应用——数据结构:堆的实现,以及堆的应用:如堆排序,又或者TOP-K问题;
感谢移置残风的主页:残风也想永存-CSDN博客,❤❤❤
一、堆的定义
- 堆的定义:堆是一颗完全二叉树,且所有的父亲结点与子结点有相同的大小关系。
- 大堆:所有的父亲结点的值 都比 子结点要大。
- 小堆:所有的父亲结点的值 都比 子结点要小。
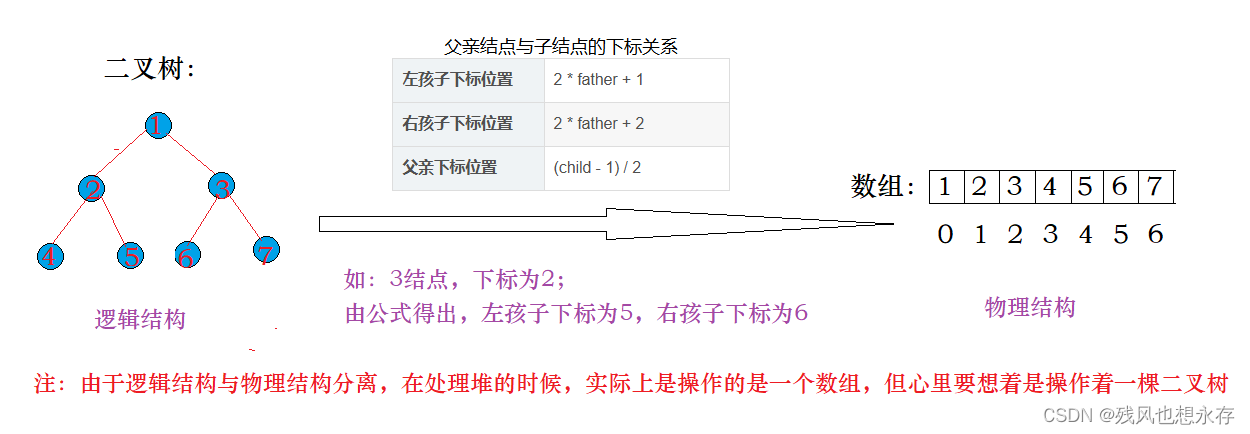
上期,我们讲过,对于完全二叉树,若用数组的下标0,1,2...,从左到右依次表示第一层,第二层...,则父亲结点与子结点的关系,可用下标表示出来。
而堆本身就是一种特殊的完全二叉树,所以用顺序结构表示堆,再简单不过~
二、堆的实现讲解
//堆的结构体声明与定义
typedef int HpDateType;
typedef struct Heap
{
HpDateType* date;
size_t size;
size_t capacity;
}Heap;
//堆的函数接口声明:
void HeapInit(Heap* php);//初始化
void HeapDestory(Heap* php);//销毁
void HeapPush(Heap* php, HpDateType x);//插入
void HeapPop(Heap* php);//删除堆顶的元素
HpDateType HeapTop(Heap* php);//返回堆顶元素
size_t HeapSize(Heap* php);//返回堆的数据个数
bool HeapEmpty(Heap* php);//判空//以下为上面函数接口的子函数,其目的是插入或
//删除元素后,符合堆的定义——但因其重要性~,下面会着重讲解
void AdjustUp(HpDateType* a, int n);//向上调整算法
void AdjustDown(HpDateType* a, int n, int size);向下调整算法
通过上面的声明,可以清楚的发现,其堆的实现,和动态顺序表的实现,极为相似;但又有一些区别; 比如在插入数据的时候,我们并不只是在最后一个数据的后面插入一个数据就行了,而是要通过向上调整算法,保持其符合堆的定义;在删除数据的时候,我们也不是删除最后一个数据,而是删除堆顶的元素。
1.向上调整算法
i.实现思路讲解
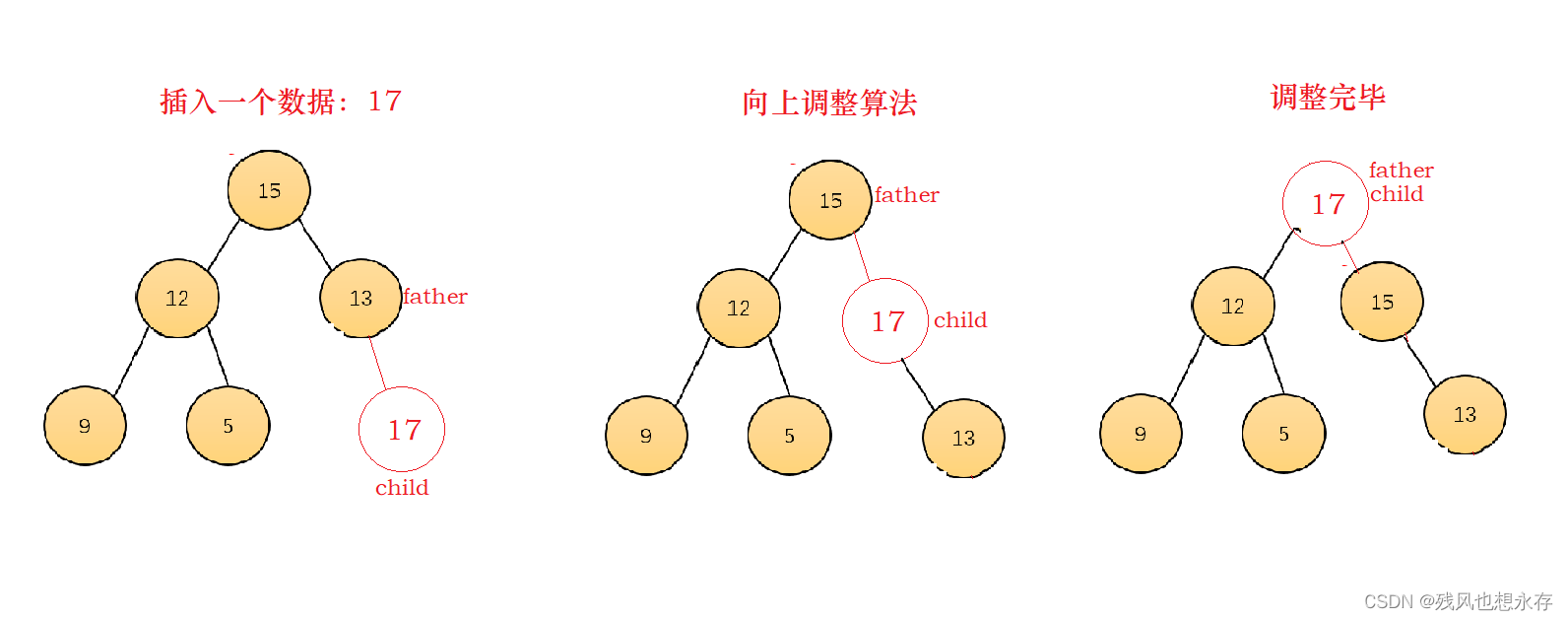
应用效果:给你一个堆,在尾部任意插入元素,将该结点调整到适合他的位置,大堆,比父亲小;若是小堆,比父亲小。
(建大堆)将插入得新结点,与其父亲做比较,若比父亲大,则交换数据,进行下一次循环,若比父亲小,或该结点的下标到0位置,则调整完毕,循环结束。
ii.复杂度
向上调整算法:最坏的情况,为调整高度次,假设二叉树的有N个结点,所以时间复杂度为O(logN)。

iii.代码
void AdjustUp(HpDateType* a, int n)
{assert(a);int child = n;int father = (child - 1) / 2;while (child > 0){// 大堆if (a[child] > a[father]){Swap(&a[father], &a[child]);child = father;father = (child - 1) / 2;}else break;}
}2.向下调整算法
i.实现思路讲解
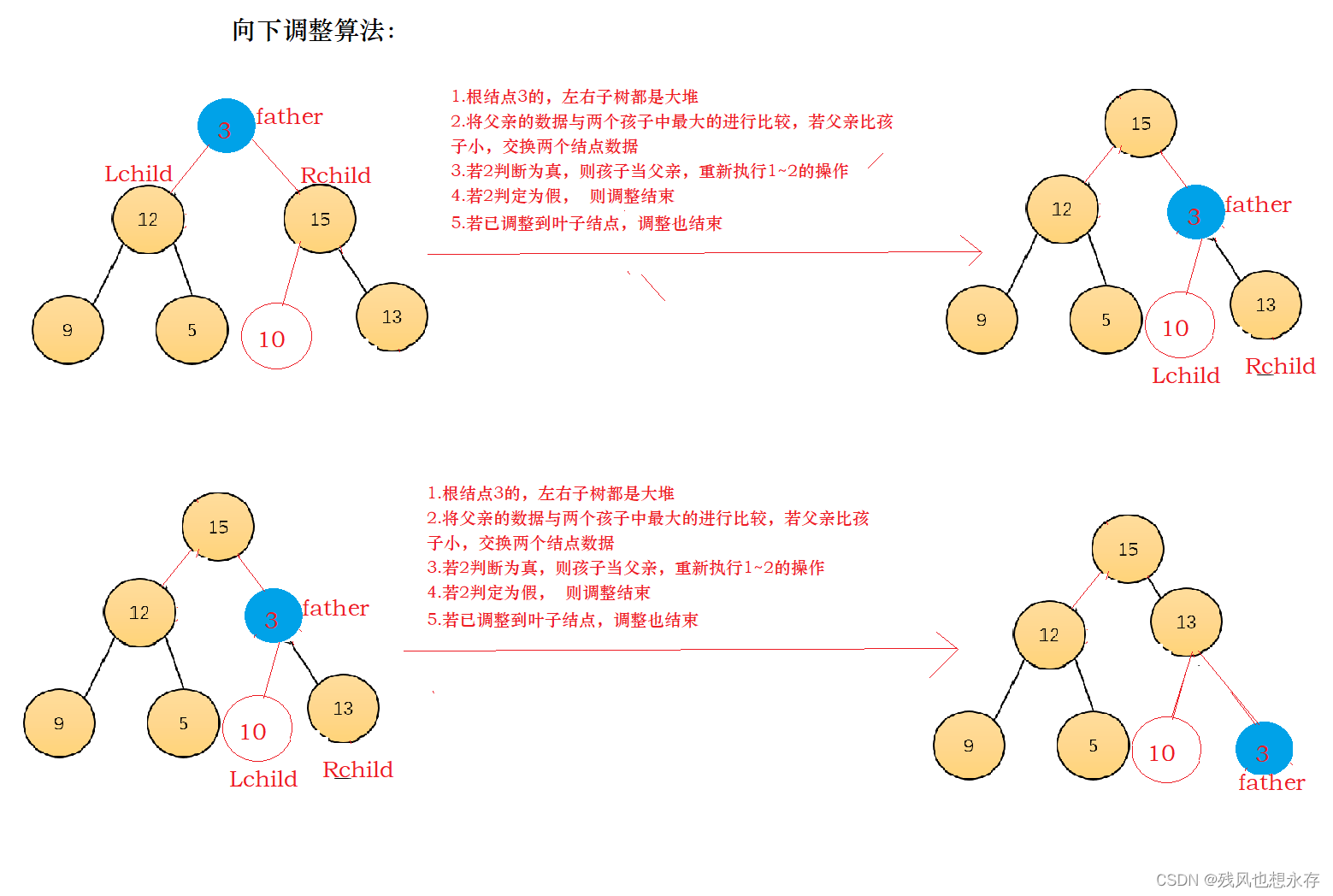
向下调整算法使用前提:左右子树是相同的堆,若是建小堆,左右子树都是小堆,才可使用向下调整算法;
ii.时间复杂度推导
向下调整算法:最坏的情况,为调整高度次,假设二叉树的有N个结点,所以时间复杂度为O(logN)。

iii.代码
void AdjustDown(HpDateType* a, int n, int size)
{assert(a);int father = n;int child = 2 * father + 1;while (2 * father + 1 < size){// 左孩子比父亲大的假设不成立if (child + 1 < size && a[child] < a[child + 1]){child += 1;}// 大堆if (a[child] > a[father]){Swap(&a[child], &a[father]);father = child;child = 2 * father + 1;}elsebreak;}
}3.插入元素
在插入数据的时候,我们并不只是在最后一个数据的后面插入一个数据就行了,而是要通过向上调整算法,保持其符合堆的定义;
void HeapPush(Heap* php, HpDateType x)
{assert(php);//查容 & 扩容 if (php->size == php->capacity){size_t newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HpDateType* tmp = (HpDateType*)realloc(php->date, newcapacity * sizeof(HpDateType));if (!tmp){perror("realloc mistake");exit(-1);}php->date = tmp;php->capacity = newcapacity;}//插入php->date[php->size++] = x;//向上调整堆;AdjustUp(php->date, php->size - 1);
}4.删除堆顶元素
在删除数据的时候,我们也不是删除最后一个数据,而是删除堆顶的元素。且要通过向下调整算法,保持其符合堆的定义;
void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);//踹走堆顶元素;Swap(&php->date[0], &php->date[php->size-1]);php->size--;//向下调整堆AdjustDown(php->date, 0, php->size);
}三、实现堆的源码
1.Heap.h
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>
#include<time.h>
#include<assert.h>typedef int HpDateType;typedef struct Heap
{HpDateType* date;size_t size;size_t capacity;
}Heap;void HeapInit(Heap* php);//初始化
void HeapDestory(Heap* php);//销毁
void HeapPush(Heap* php, HpDateType x);//插入
void HeapPop(Heap* php);//删除
HpDateType HeapTop(Heap* php);//返回堆顶元素
size_t HeapSize(Heap* php);//返回堆的数据个数
bool HeapEmpty(Heap* php);//判空void AdjustUp(HpDateType* a, int n);
void AdjustDown(HpDateType* a, int n, int size);2.Heap.c
#define _CRT_SECURE_NO_WARNINGS 1#include"Heap.h"void HeapInit(Heap* php)
{assert(php);php->date = NULL;php->size = php->capacity = 0;
}void HeapDestory(Heap* php)
{assert(php);free(php->date);php->date = NULL;php->size = php->capacity = 0;
}void Swap(HpDateType* e1, HpDateType* e2)
{int tmp = *e1;*e1 = *e2;*e2 = tmp;
}void AdjustUp(HpDateType* a, int n)
{assert(a);int child = n;int father = (child - 1) / 2;while (child > 0){// 小堆if (a[child] < a[father]){Swap(&a[father], &a[child]);child = father;father = (child - 1) / 2;}else {break;} }
}void HeapPush(Heap* php, HpDateType x)
{assert(php);//查容 & 扩容 if (php->size == php->capacity){size_t newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HpDateType* tmp = (HpDateType*)realloc(php->date, newcapacity * sizeof(HpDateType));if (!tmp){perror("realloc mistake");exit(-1);}php->date = tmp;php->capacity = newcapacity;}//插入php->date[php->size++] = x;//向上调整堆;AdjustUp(php->date, php->size - 1);
}void AdjustDown(HpDateType* a, int n, int size)
{assert(a);int father = n;int child = 2 * father + 1;while (2 * father + 1 < size){// 左孩子比父亲小的假设不成立if (child + 1 < size && a[child] > a[child + 1]){child += 1;}// 小堆if (a[child] < a[father]){Swap(&a[child], &a[father]);father = child;child = 2 * father + 1;}else{break;}}
}void HeapPop(Heap* php)
{assert(php);assert(php->size > 0);//踹走堆顶元素;Swap(&php->date[0], &php->date[php->size-1]);php->size--;//向下调整堆AdjustDown(php->date, 0, php->size);
}HpDateType HeapTop(Heap* php)
{assert(php);return php->date[0];
}size_t HeapSize(Heap* php)
{assert(php);return php->size;
}
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}四、堆的应用
1.建堆
i.向上调整建堆(时间复杂度推导)
问题:给你一个数组,返回一个大堆;
问起建堆,可能你们会说,创建一个堆的数据结构,然后不断的Push就行了;可是空间复杂度却是O(N),我们如何在空间复杂度O(1)的情况下,建一个堆呢?
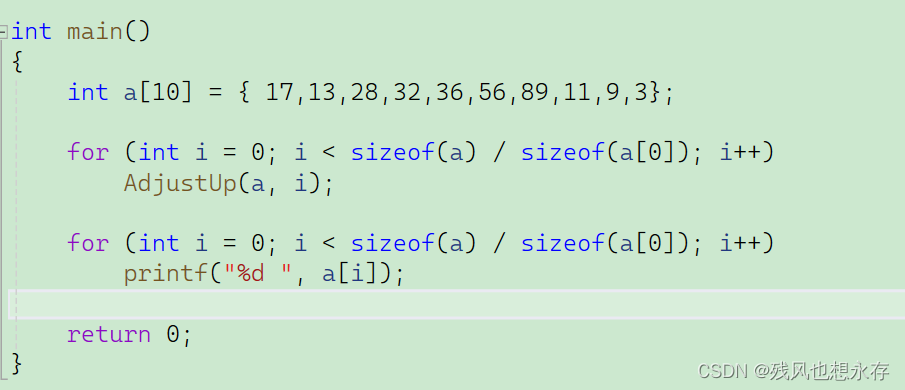
HeapPush的时候,是在堆尾插入一个数据,然后向上调整,而我们其实可以省去插入的过程,在给定数组的上面,只使用向上调整算法,实现建堆;
省去了开辟空间的消耗,空间复杂度为O(1);时间复杂度为O(NlogN)


ii. 向下调整建堆(时间复杂度推导)
向上调整建堆的时间复杂度为O(NlogN),若面试官说O(NlogN),不好,问你能否将时间复杂度?你是否会觉得不可思议?而你又会如何解决呢?我们大脑的思维很难凭空创造,但我们可以从已有的问题,得到启发;下面我们重新分析一下向上调整建堆时间浪费在何处,
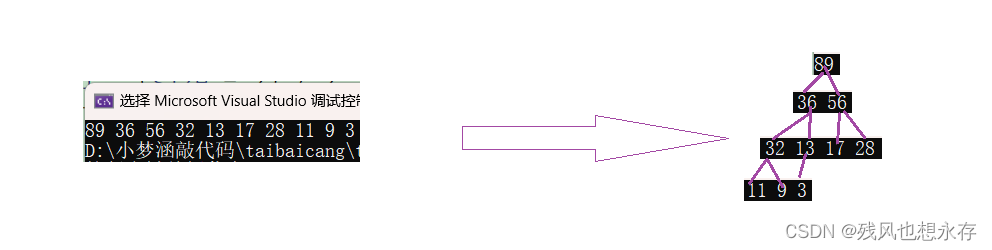
我们会发现,层数越高结点,最坏调整次数越高,与此同时,结点个数也越多,我说这可能是问题的突破高,我们如何让调整次数多的结点,个数减少呢?我们会想到向下调整算法,向下调整算法,有个使用前提:左右子树是相同的堆,才可使用向下调整算法。所以我们可以从最后一个非叶子结点往前调整;如上图,先向下调整28结点,依次往前13、56、32、...、到最后的根结点。
优点:结点个数越多的那一层,向下调整次数反而越少;时间复杂度为O(N)


相关文章:

二叉树第二期:堆的实现与应用
若对树与二叉树的相关概念,不太熟悉的同学,可移置上一期博客 链接:二叉树第一期:树与二叉树的概念-CSDN博客 本博客目标:对二叉树的顺序结构,进行深入且具体的讲解,同时学习二叉树顺序结构的应用…...

python-求出 e 的值
[题目描述] 利用公式 e11/1!1/2!1/3!⋯1/𝑛!,求 e 的值,要求保留小数点后 10 位。输入: 输入只有一行,该行包含一个整数 n,表示计算 e 时累加到1/n!。输出: 输出只有一行,该行包含计…...

模型微调方法
文章目录 LoRADoRAMoRA 以下部分参考自: https://mp.weixin.qq.com/s/OxYNpXcyHF57OShQC26n4g LoRA LoRA是微软于2021年推出的一种经济型微调模型参数的方法。 它在冻结大部分的模型参数的情况下,仅仅更新额外的部分参数。其性能与全参数微调相似。 LoRA假设微调期间…...

cesium使用cesium-navigation-es6插件创建指南针比例尺
cesium-navigation-es6 是一个为 Cesium.js 提供导航控件的库,它提供了一些常见的用户界面组件,用于在 Cesium 场景中实现用户导航和交互。下面将介绍如何在项目中使用 cesium-navigation-es6。 使用步骤 1. 安装 cesium-navigation-es6 首先…...
Sync.Map)
go sync包(七)Sync.Map
Sync.Map 原理 通过 read 和 dirty 两个字段实现数据的读写分离,读的数据存在只读字段 read 上,将最新写入的数据存在 dirty 字段上。读取时会先查询 read,不存在再查询 dirty,写入时则只写入 dirty。读取 read 并不需要加锁&am…...

Batch文件中的goto命令:控制流程的艺术
Batch文件,也称为批处理脚本,是Windows操作系统中用于自动化任务的一种脚本文件。在Batch脚本中,goto命令是一个至关重要的控制结构,它允许脚本跳转到指定的标签位置,从而实现循环、条件分支等复杂的控制流程。本文将详…...

【chatgpt】两层gcn提取最后一层节点输出特征,如何自定义简单数据集
文章目录 两层gcn,提取最后一层节点输出特征,10个节点,每个节点8个特征,连接关系随机生成(无全连接层)如何计算MSE 100个样本,并且使用批量大小为32进行训练第一个版本定义数据集出错࿰…...

Java面试题:讨论你如何保持对Java生态系统中新技术的了解
保持对Java生态系统中新技术的了解可以通过以下几种方法: 官方资源: Oracle的官方博客和新闻:Oracle是Java的主要维护者,其官方网站和博客会定期发布Java的新版本、功能更新和最佳实践。Java SE Documentation:Java官方…...
和Swin Transformer)
深度学习之Transformer模型的Vision Transformer(ViT)和Swin Transformer
Transformer 模型最初由 Vaswani 等人在 2017 年提出,是一种基于自注意力机制的深度学习模型。它在自然语言处理(NLP)领域取得了巨大成功,并且也逐渐被应用到计算机视觉任务中。以下是两种在计算机视觉领域中非常重要的 Transformer 模型:Vision Transformer(ViT)和 Swi…...
玩个游戏 找以下2个wordpress外贸主题的不同 你几找到几处
Aitken艾特肯wordpress外贸主题 适合中国产品出海的蓝色风格wordpress外贸主题,产品多图展示、可自定义显示产品详细参数。 https://www.jianzhanpress.com/?p7060 Ultra奥创工业装备公司wordpress主题 蓝色风格wordpress主题,适合装备制造、工业设备…...

React Native优质开源项目推荐与解析
目录 2. React Native的优势 2.1. 跨平台开发 2.2. 热更新 2.3. 丰富的社区资源 2.4. 优秀的性能 3. 优质开源项目推荐 3.1. React Navigation 3.1.1 项目简介 3.1.2 特点和优势 3.1.3 应用场景 3.2. Redux 3.2.1 项目简介 3.2.2 特点和优势 3.2.3 应用场景 3.3…...
树莓派安装windows系统
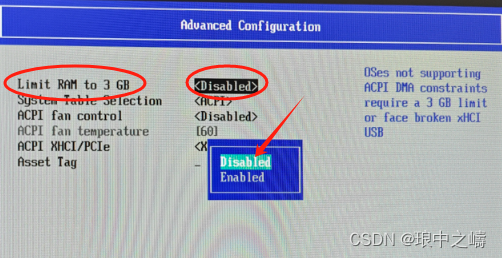
第1步: https://uupdump.net/下载对应的系统文件,所有选择项都默认选择。 第2步: 解压下载后的文件,双击运行下面文件。等待下载完成,等待过程很漫长,很考验耐心。 第3步: 提示已经finish了&…...

CSS-position/transform
1 需求 2 语法 在CSS中,positioning 和 transform 是两个非常重要的概念,它们分别用于控制元素在页面上的布局和变换。 Positioning CSS中的position属性用于设置元素的定位类型。它有几个值,包括: static:这是默认…...

面试题之一
路由的两种模式:hash模式和 history模式。 两种的区别、如何实现。 hash模式中#的作用 vue性能优化。具体如何实现(回答了一个可以函数引入的方法引入路由。问) keep-alive 说一下EventBus CSS: flex布局 css新特性 盒子模型 J…...

494. 目标和 Medium
给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添加 - ,然…...

如何实现灌区闸门控制自动化?宏电“灌区哨兵”为灌区闸门控制添“智慧”动能
闸门控制站是节水灌溉工程中的重要组成部分。随着科技的不断进步和农田水利现代化的发展,传统的闸门控制和管理手段已经不能满足现代农业的发展要求。以宏电“灌区哨兵”为核心的闸门自动化控制系统,能有效解决灌区闸门距离远、数量多、不易操作、不好监…...

PHP电商系统开发指南数据库管理
回答:数据库管理是电商系统开发的关键,涉及数据的存储、管理和检索。选择合适的数据库引擎,如mysql或 postgresql。创建数据库架构,定义数据的组织方式(如产品表、订单表)。进行数据建模,考虑实…...

基于Vue.js的电商前端模板:Vue-Dashboard-Template的设计与实现
摘要 随着电子商务的飞速发展,前端页面的设计和实现变得愈发重要。本文介绍了一个基于Vue.js的电商前端模板——Vue-Dashboard-Template,旨在提供一个高性能、易扩展的电商平台前端解决方案。该模板遵循响应式设计、模块化、组件化开发等设计原则&#…...

论文解读:【CVPR2024】DUSt3R: Geometric 3D Vision Made Easy
论文“”https://openaccess.thecvf.com/content/CVPR2024/papers/Wang_DUSt3R_Geometric_3D_Vision_Made_Easy_CVPR_2024_paper.pdf 代码:GitHub - naver/dust3r: DUSt3R: Geometric 3D Vision Made Easy DUSt3R是一种旨在简化几何3D视觉任务的新框架。作者着重于…...

springboot助农电商系统-计算机毕业设计源码08655
摘要 近年来,电子商务的快速发展引起了行业和学术界的高度关注。基于移动端的助农电商系统旨在为用户提供一个简单、高效、便捷的农产品购物体验,它不仅要求用户清晰地查看所需信息,而且还要求界面设计精美,使得功能与页面完美融合…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
