Studying-代码随想录训练营day24| 93.复原IP地址、78.子集、90.子集II
第24天,回溯算法part03,牢记回溯三部曲,掌握树形结构结题方法💪
目录
93.复原IP地址
78.子集
90.子集II
总结
93.复原IP地址
文档讲解:代码随想录复原IP地址
视频讲解:手撕复原IP地址
题目:

学习:本题属于切割类问题,不同的是本题需要使用 ' · ’ 来切割,并且本题对切割的数字大小和多少,切割多少次都有要求。但本质都是两步:1.切割;2.判断切割是否正确。
依据以上两点,本题和131.分割回文串不同的地方就在于对分割部分的判断和终止条件的选择。回溯逻辑用树形结构来表示为:
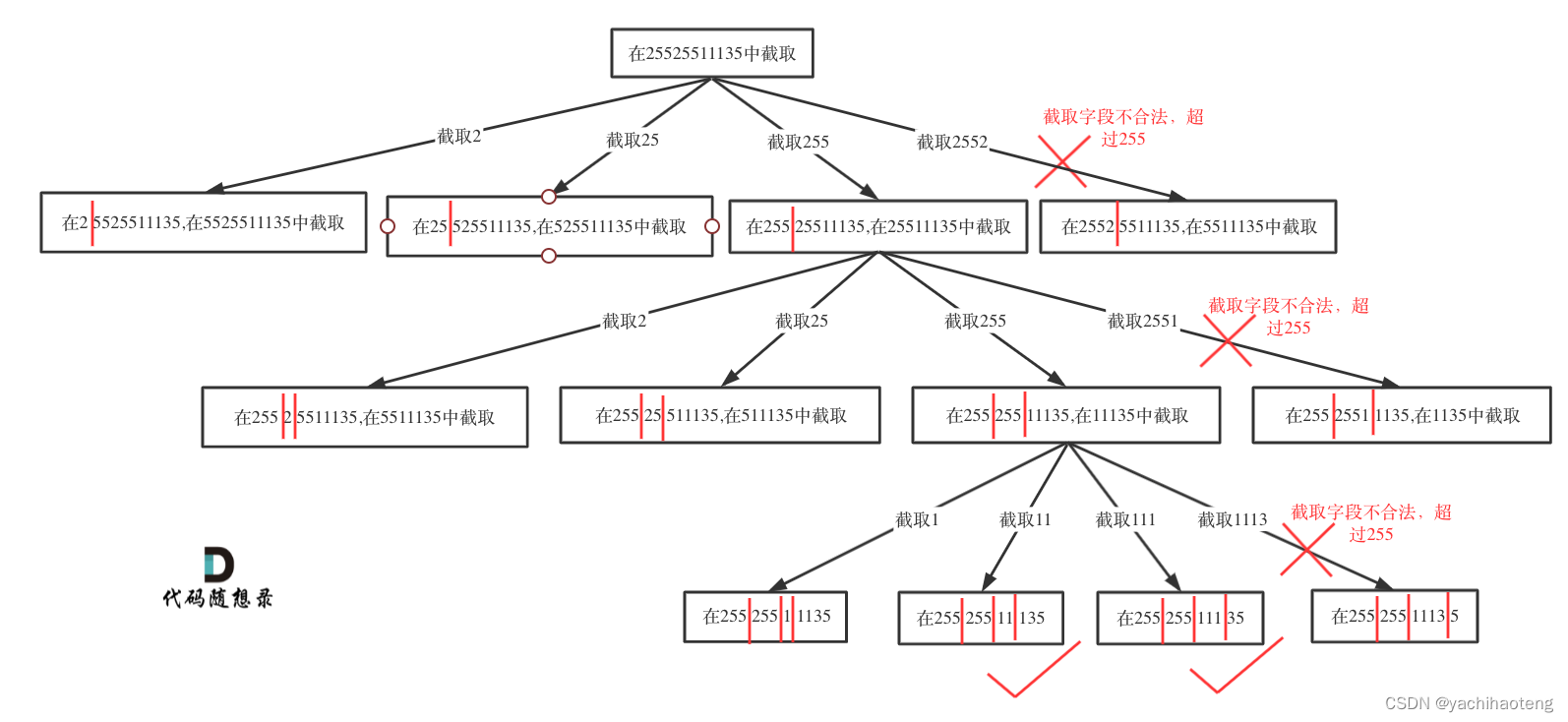
注意:判断分割部分是否合法,主要从三个部分出发:1.段位以0为开头且不止有0的数字不合法。2.段位里有非正整数字符不合法。3.段位如果大于255了不合法。
代码:确定回溯三部曲,注意本题要在字符串中加入' . ' 因此回溯的时候要删掉该点。
//时间复杂度O(3^4)
//空间复杂度O(n)
class Solution {
public://直接在字符串上进行操作,因此不设置路径数组vector<string> result; //返回数组//确定返回值和参数列表,直接在答案数组中插入因此不需要返回值,参数中需要原字符串s,分割点startindex//本题还需要一个int型变量point表示当前逗号的数量void backtracking(string& s, int startindex, int point) {//确定终止条件,当逗号数量为3个时,说明当前分割已经完成了if(point == 3) {//最后一部分字符串还需要进行判断if(ipvaild(s, startindex, s.size() - 1)) {result.push_back(s);}return;}//确定单层递归逻辑for(int i = startindex; i < s.size(); i++) {//startindex作为切割线,切割的字符串区间为[startindex, i],左闭右闭//判断切割下来的字符串是否合理if(ipvaild(s, startindex, i)){//如果合理的话,在字符串下标i后插入逗号,并进行下一轮递归s.insert(s.begin() + i + 1, '.');point++;//注意这里需要传入的是i+2,因为加了一个逗号,切割的位置需要往后移两位backtracking(s, i + 2, point);point--; //回溯s.erase(s.begin() + i + 1);}else { //假如不满足,后续的切割方法也难以满足,直接跳出本层循环break;}}}bool ipvaild(string& s, int start, int end) {if (start > end) {return false;}//如果存在前置0的话,返回falseif(start != end && s[start] == '0') {return false;}int num = 0; //对切割字符串进行求和for(int i = start; i <= end; i++) {if(s[i] - '0' < 0 || s[i] - '0' > 9) {return false;}num = num * 10 + (s[i] - '0');if(num > 255) {return false;}}return true;}vector<string> restoreIpAddresses(string s) {backtracking(s, 0, 0);return result;}
};本题可以进行剪枝,自认为本题可以从三个部分进行剪枝,分别是:1.剪枝1,给的字符串不满足切割有效的IP地址;2.剪枝2,分割实际只需要分割3个字符就行,缩小循环范围;3.每次切割后可以判断一下是否后面的字符还能够满足切割要求。
代码:
class Solution {
public://切割问题主要需要两点:切割,判断!//直接在字符串上进行操作,因此不设置路径数组vector<string> result; //返回数组//确定返回值和参数列表,直接在答案数组中插入因此不需要返回值,参数中需要原字符串s,分割点startindex//本题还需要一个int型变量point表示当前逗号的数量void backtracking(string& s, int startindex, int point) {//确定终止条件,当逗号数量为3个时,说明当前分割已经完成了if(point == 3) {//最后一部分字符串还需要进行判断if(ipvaild(s, startindex, s.size() - 1)) {result.push_back(s);}return;}//确定单层递归逻辑//剪枝2,分割只需要分割3个数字就够了for(int i = startindex; i < startindex + 3; i++) {//剪枝3,后续剩余的节点数不满足切割要求if(s.size() - startindex > (4 - point) * 3 || s.size() - startindex < (4 - point)) {break;}//startindex作为切割线,切割的字符串区间为[startindex, i],左闭右闭//判断切割下来的字符串是否合理if(ipvaild(s, startindex, i)){//如果合理的话,在字符串下标i后插入逗号,并进行下一轮递归s.insert(s.begin() + i + 1, '.');point++;//注意这里需要传入的是i+2,因为加了一个逗号,切割的位置需要往后移两位backtracking(s, i + 2, point);point--; //回溯s.erase(s.begin() + i + 1);}else { //假如不满足,后续的切割方法也难以满足,直接跳出本层循环break;}}}bool ipvaild(string& s, int start, int end) {if (start > end) {return false;}//如果存在前置0的话,返回falseif(start != end && s[start] == '0') {return false;}int num = 0; //对切割字符串进行求和for(int i = start; i <= end; i++) {if(s[i] - '0' < 0 || s[i] - '0' > 9) {return false;}num = num * 10 + (s[i] - '0');if(num > 255) {return false;}}return true;}vector<string> restoreIpAddresses(string s) {//剪枝1,给的字符串不满足切割有效的ip地址if(s.size() < 4 || s.size() > 12) return result;backtracking(s, 0, 0);return result;}
};78.子集
文档讲解:代码随想录子集
视频讲解:手撕子集问题
题目:
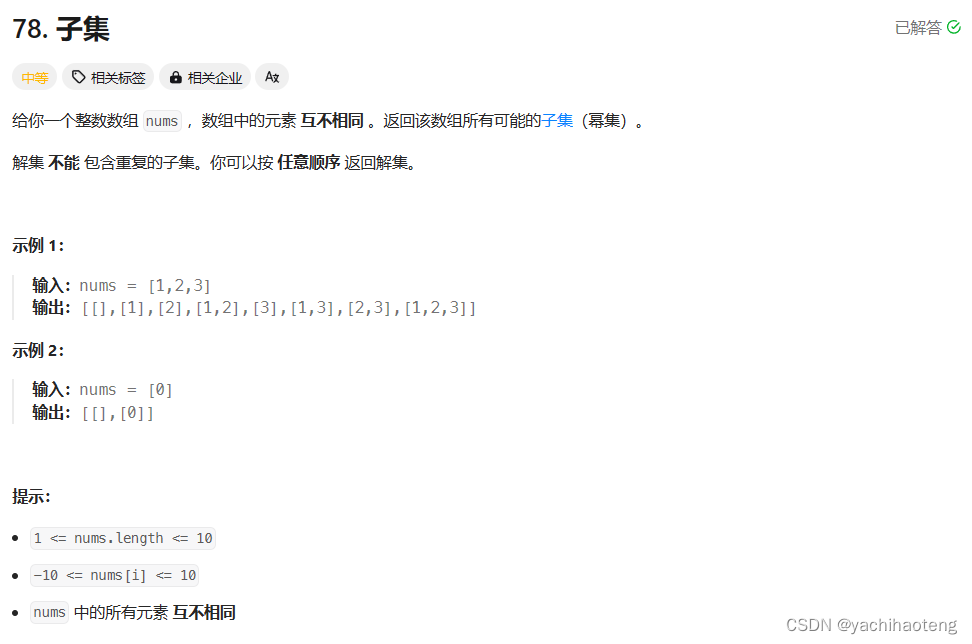
学习:回溯算法能够解决的第三类问题,子集问题。子集问题与切割问题和组合问题的本质不同在于,切割问题和组合问题都是在叶子节点收获结果,但是子集问题需要在每个节点都收获结果,这也导致了子集问题对result数组push_back的位置不同,但其他部分其实几乎是一致的。子集问题其实也能看作是一个组合问题,因此也需要注意去重。回溯逻辑转化为树形结构为:
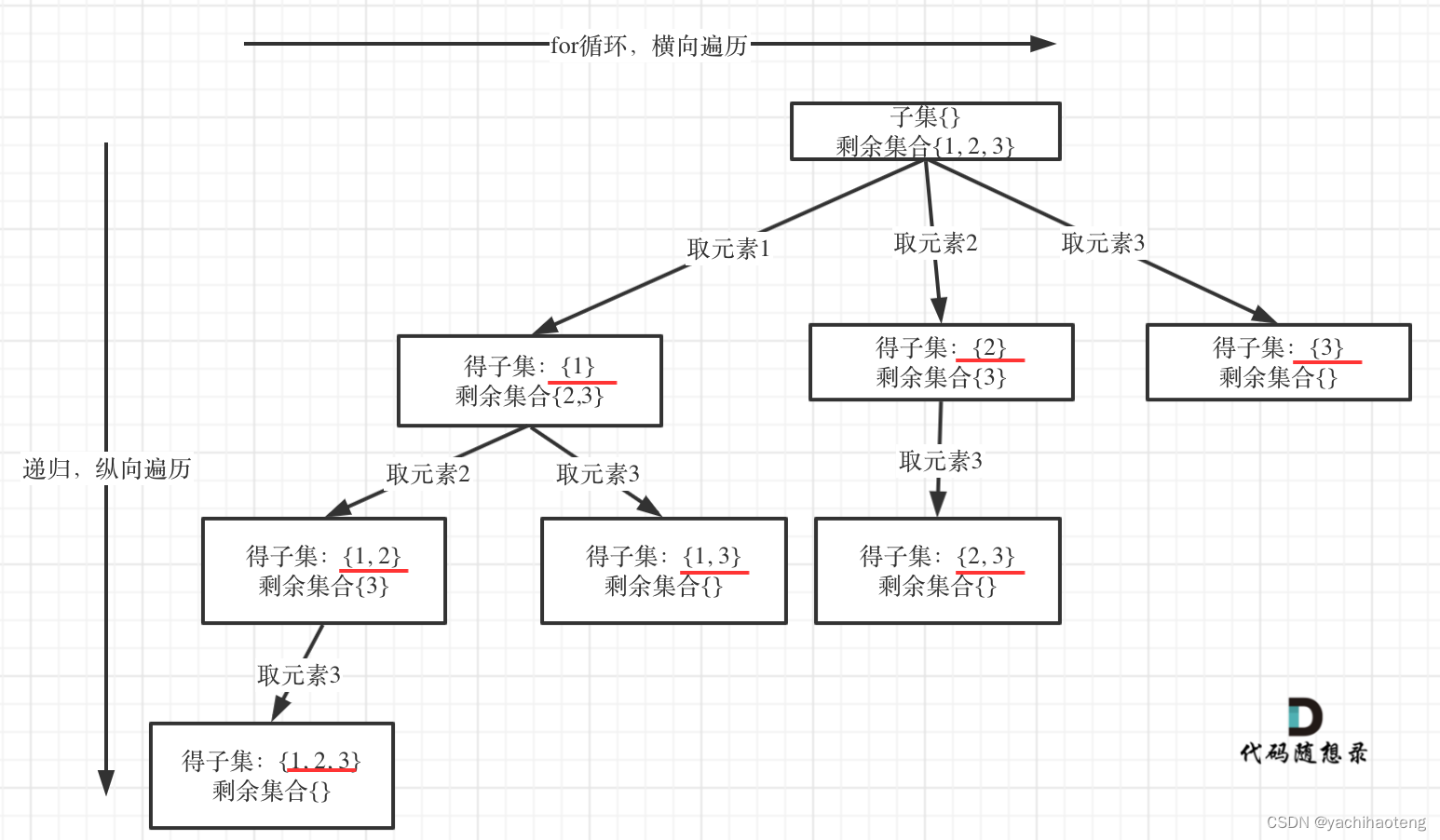
代码:确定回溯三部曲
//时间复杂度O(n*2^n)
//空间复杂度O(n)
class Solution {
public:vector<vector<int>> result; //返回数组vector<int> path; //保存路径//确定返回值和参数列表,在数组中直接进行操作,所以不需要返回值,参数列表需要遍历的数组和当前遍历的下标void backtracking(vector<int>& nums, int startindex) {//子集问题的不同在于,子集收获答案是在每个节点均收货一次//在终止条件前,先进行收获,其中也包含了空集result.push_back(path);//确定终止条件(其实等于就可以了),遍历到最后//该终止条件也可以不写,因为当startindex >= nums.size()时,下面的for循环也不会进入,但要注意for循环后加return。if(startindex >= nums.size()) {return;}//确定单层递归逻辑for(int i = startindex; i < nums.size(); i++) {path.push_back(nums[i]);//传入i+1,防止出现重复backtracking(nums, i + 1);path.pop_back();}return;}vector<vector<int>> subsets(vector<int>& nums) {backtracking(nums, 0);return result;}
};90.子集II
文档讲解:代码随想录子集II
视频讲解:手撕子集II
题目:

学习:本题和上一题不同点在于本题存在重复元素,需要对后续的相同元素进行去重,事实上本题和组合总和II的去重是相同的,本质都是如果后面出现了与前面相同的元素就可以跳过该元素的遍历,因为前面的元素一定把后面的元素还有的组合都包括的。基于此本题可以采取和40.组合总和II相同的去重方式,都是在树层进行去重。
代码:确定回溯三部曲
//时间复杂度O(n*2^n)
//空间复杂度O(n)
class Solution {
public: vector<vector<int>> result; //返回答案数组vector<int> path; //保存路径//确定参数和返回值void backtracking(vector<int>& nums, int startindex) {//收集每一个节点result.push_back(path);//确定终止条件if(startindex == nums.size()) {return;}//确定单层递归逻辑for(int i = startindex; i < nums.size(); i++) {//去重if(i > startindex && nums[i] == nums[i-1]){continue;}path.push_back(nums[i]);backtracking(nums, i + 1);path.pop_back();}return;}vector<vector<int>> subsetsWithDup(vector<int>& nums) {//进行排序,便于去重sort(nums.begin(), nums.end());backtracking(nums, 0);return result;}
};总结
切割问题首尾,子集问题开始,牢记子集问题和切割问题和组合问题的不同。
相关文章:

Studying-代码随想录训练营day24| 93.复原IP地址、78.子集、90.子集II
第24天,回溯算法part03,牢记回溯三部曲,掌握树形结构结题方法💪 目录 93.复原IP地址 78.子集 90.子集II 总结 93.复原IP地址 文档讲解:代码随想录复原IP地址 视频讲解:手撕复原IP地址 题目࿱…...

2024《汽车出海全产业数据安全合规发展白皮书》下载
随着中国制造向中国智造目标的迈进,中国汽车正以前所未有的速度和质量,在全球市场上开疆拓土。不过,在中国汽车加快出海步伐的过程中,数据安全合规风险管理成为车企不容忽视的课题。 6月25日,在中国(上海&…...
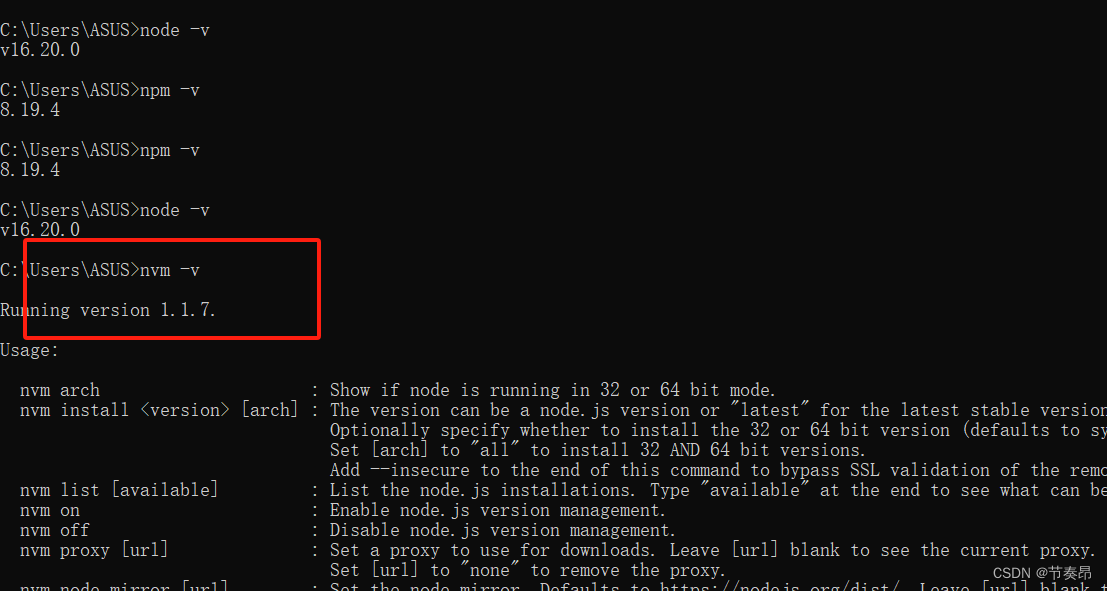
nvm安装以及idea下vue启动项目过程和注意事项
注意1:nvm版本不要太低,1.1.7会出现下面这个问题,建议1.1.10及其以上版本 然后安装这个教程安装nvm和node.js 链接: nvm安装教程(一篇文章所有问题全搞定,非常详细) 注意2:上面的教程有一步骤…...

Java SPI服务发现与扩展的利器
Java中,为了实现模块之间的解耦和可扩展性,我们常常需要一种机制来动态加载和替换实现。Java SPI就是这样一种机制,它允许我们在不修改原有代码的情况下,为接口添加新的实现,并在运行时动态加载它们。 SPI,…...

Ansible的Playbook
Playbook 特点 playbook 剧本是由一个或多个"play"组成的列表play的主要功能在于将预定义的一组主机,装扮成事先通过ansible中的task定义好的任务角色。Task实际是调用ansible的一个module,将多个play组织在一个playbook中,即可以让…...

多平台自动养号【开心版】偷偷使用就行了!
大家好,今天我无意间发现了一款【多平台自动养号工具】,看了一下里面的功能还是挺全面的,包含了【抖音,快手,小红薯】还有一些截流功能 虽然这款工具功能强大,但美中不足的是需要付费的。但别担心…...

Android与JavaScript的交互,以实现从WebView中打开原生页面并传递参数
在Android应用中,实现Android与JavaScript的交互,以实现从WebView中打开原生页面并传递参数,可以通过以下详细步骤完成: 1. 准备工作 添加WebView至布局:在你的Activity或Fragment的XML布局文件中加入WebView控件。 …...
在计算机中是如何存储及显示的)
信息(文字、图像、音频、视频等)在计算机中是如何存储及显示的
信息(文字、图像、音频、视频等)在计算机中是如何存储及显示的 图片的存储图片的文件格式像素数据的二进制表示存储和处理显示总结 图片的显示4. 像素点控制具体的像素控制过程示例总结 如题,这里以图片为例。 图片的存储 计算机桌面上的一…...

【考研408计算机组成原理】微程序设计重要考点指令流水线考研真题+考点分析
苏泽 “弃工从研”的路上很孤独,于是我记下了些许笔记相伴,希望能够帮助到大家 目录 微指令的形成方式 微指令的地址形成方式 对应考题 题目:微指令的地址形成方式 - 断定方式 解题思路: 答题: 分析考点&…...

查看哪个docker环境在占用gpu
前言 有时候发现某些docker占用gpu资源却没有训练,需要查清楚是哪个并且把它stop掉。 方法 在docker里面用nvidia-smi命令,没有pid显示,需要在外面使用。得到pid信息后,使用命令 docker top 15766f6eeaf7(容器ID) | grep 551…...

JVM相关总结
JVM的些许问题 1.JVM内存区域划分 2.JVM类加载过程 3.JVM的垃圾回收机制 1.JVM的内存区域划分 一个运行起来的Java进程就是一个JVM虚拟机,需要从操作系统申请一大片内存,就会把内存划分成几个区域,每个区域都有不同的作用 常见的面试题 2.JVM类加载过程 熟练背诵 ! ! !…...

Python 面试【初级】
欢迎莅临我的博客 💝💝💝,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

机器学习SVR 随机森林 RBF神经网络做回归预测的MATLAB代码
SVR 参考这篇文章 Libsvm使用笔记【matlab】 close all; clc clear %% 下载数据 load(p_train.mat); load(p_test.mat); load(t_train.mat); load(t_test.mat); %% 数据归一化 %输入样本归一化 [pn_train,ps1] mapminmax(p_train); pn_train pn_train; pn_test mapminma…...

Spring Boot中配置Swagger用于API文档
Spring Boot中配置Swagger用于API文档 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中配置Swagger,以便于快…...

学习java第一百一十六天
Spring Framework有哪些不同的功能? 答: 轻量级-Spring 在代码量和透明度方面都很轻便。 IOC-控制反转AOP-面向切面编程可以将应用业务逻辑和系统服务分离,以实现高内聚。容器-Spring 负责创建和管理对象(Bean)的生命周…...
全面解析)
SQL Server的隐私盾牌:动态数据屏蔽(DMS)全面解析
🛡️ SQL Server的隐私盾牌:动态数据屏蔽(DMS)全面解析 在数据驱动的商业世界中,保护敏感信息至关重要。SQL Server提供了一种强大的安全特性——动态数据屏蔽(Dynamic Data Masking,简称DMS),…...

Android中常见的线程池
日常开发中我们常常使用到线程池,其能有效管理线程资源,避免过多线程导致系统资源浪费、又能复用线程资源,避免频繁的创建/销毁线程。在Android中线程池的实现为ThreadPoolExecutor类,本文主要记录该类相关的知识点。 线程池的六…...

C# YoloV8 模型效果验证工具(OnnxRuntime+ByteTrack推理)
C# YoloV8 模型效果验证工具(OnnxRuntimeByteTrack推理) 目录 效果 项目 代码 下载 效果 模型效果验证工具 项目 代码 using ByteTrack; using OpenCvSharp; using System; using System.Collections.Generic; using System.Diagnostics; using System.Drawing; using Sys…...
什么是Cookie?有什么用?如何清除浏览器中的Cookie?
互联网上的每一次点击和每一个选择都可能被一种名为Cookie的技术记录下来。但Cookie是什么?我们在网站上登录时,为什么经常会被问及是否接受Cookie?接受Cookie登录会不会影响我们的在线隐私? Cookie是什么? Cookie是一…...

数据库基本管理
数据完整性: 实体完整性:每一行必须是唯一的实体域完整性:检查每一列是否有效引用完整性:确保所有表中数据的一致性,不允许引用不存在的值用户定义的完整性:制定特定的业务规则 主键: 用于唯…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
