你需要精益管理咨询公司的N+1个理由
近年来,精益管理作为一种被全球众多知名企业验证过的成功管理模式,越来越受到企业的青睐。但是,为何在实施精益管理的过程中,众多企业纷纷选择请咨询公司来协助呢?今天,我们就来一起揭秘这背后的原因。

1. 专业知识与经验
- 咨询公司通常拥有丰富的精益管理专业知识和跨行业的实践经验。他们熟悉各种精益工具和方法的应用,能够为企业提供准确的诊断和有效的解决方案。
2. 客观视角
- 作为外部机构,深圳天行健精益管理咨询公司能够以客观、中立的态度看待企业的问题和现状,不受企业内部政治、文化和历史因素的影响,提供更公正和全面的建议。
3. 定制化方案
- 能够根据企业的特定需求、行业特点和组织文化,为其量身定制精益管理的实施策略和计划,确保方案的针对性和适应性。
4. 变革推动
- 实施精益管理往往需要对企业现有的流程和文化进行变革,咨询公司可以作为外部力量,协助企业克服内部的阻力和障碍,推动变革的顺利进行。

5. 培训与能力建设
- 不仅提供方案,还可以为企业员工提供相关的培训和指导,帮助他们掌握精益管理的理念和技能,促进企业内部能力的提升。
6. 快速启动与加速进程
- 凭借其丰富的经验和资源,咨询公司能够帮助企业快速启动精益管理项目,并在实施过程中加速取得成果,缩短企业自行摸索的时间。
7. 借鉴最佳实践
- 咨询公司了解行业内的最佳实践案例,可以将这些成功经验引入企业,帮助企业少走弯路,提高精益管理实施的效果和效率。
8. 资源补充
- 在项目实施过程中,咨询公司可以补充企业内部可能短缺的专业人才和资源,确保项目的顺利推进。
然而,聘请咨询公司也并非是实施精益管理的必要条件,一些企业在具备足够的内部能力和资源的情况下,也可以自主实施精益管理,但咨询公司在很多情况下能够提供有价值的支持和帮助。
相关文章:

你需要精益管理咨询公司的N+1个理由
近年来,精益管理作为一种被全球众多知名企业验证过的成功管理模式,越来越受到企业的青睐。但是,为何在实施精益管理的过程中,众多企业纷纷选择请咨询公司来协助呢?今天,我们就来一起揭秘这背后的原因。 1. …...

[机器学习]-3 万字话清从传统神经网络到深度学习
神经网络(Neural Networks, NNs)是机器学习的一种重要方法,灵感来源于生物神经系统,由大量互联的节点(称为神经元或单元)组成,通过调整这些节点间的连接权重来学习和表示复杂的非线性关系。传统…...

网络安全等级保护2.0(等保2.0)全面解析
一、等保2.0的定义和背景 网络安全等级保护2.0(简称“等保2.0”)是我国网络安全领域的基本制度、基本策略、基本方法。它是在《中华人民共和国网络安全法》指导下,对我国网络安全等级保护制度进行的重大升级。等保2.0的发布与实施,…...
用Lobe Chat部署本地化, 搭建AI聊天机器人
Lobe Chat可以关联多个模型,可以调用外部OpenAI, gemini,通义千问等, 也可以关联内部本地大模型Ollama, 可以当作聊天对话框消息框来集成使用 安装方法参考: https://github.com/lobehub/lobe-chat https://lobehub.com/zh/docs/self-hosting/platform/…...
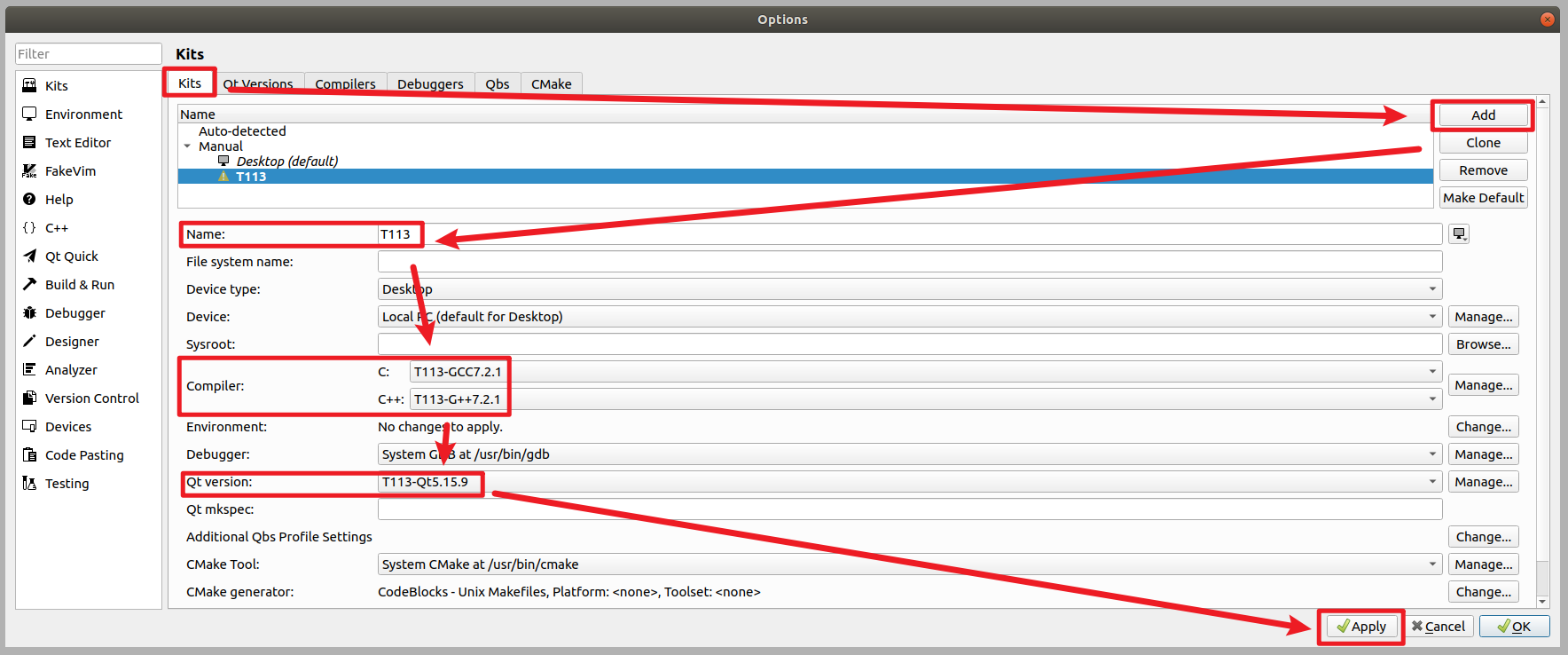
基于ARM的通用的Qt移植思路
文章目录 实验环境介绍一、确认Qt版本二、确认交叉编译工具链三、配置Qt3.1、修改qmake.conf3.2、创建autoConfig.sh配置文件 四、编译安装Qt五、移植Qt安装目录六、配置Qt creator6.1、配置qmake6.2、配置GCC编译器6.3、配置G编译器6.4、配置编译器套件6.5、创建应用 七、总结…...

IT专业入门,高考假期预习指南
七月来临,各省高考分数已揭榜完成。而高考的完结并不意味着学习的结束,而是新旅程的开始。对于有志于踏入IT领域的高考少年们,这个假期是开启探索IT世界的绝佳时机。 一、基础课程预习指南 IT专业是一个广泛的领域,涵盖了从软件开…...

芯片详解——AD7606C
芯片详解——AD7606C AD7607C 是一款由 Analog Devices(模拟器件公司)生产的 6 通道同步采样模数转换器(ADC),适用于高速数据采集系统。 工作原理 AD7607C 的工作原理主要包括以下几个步骤: 模拟信号输入:AD7607C 有六个模拟输入通道,可以同时进行采样。这些模拟信号…...
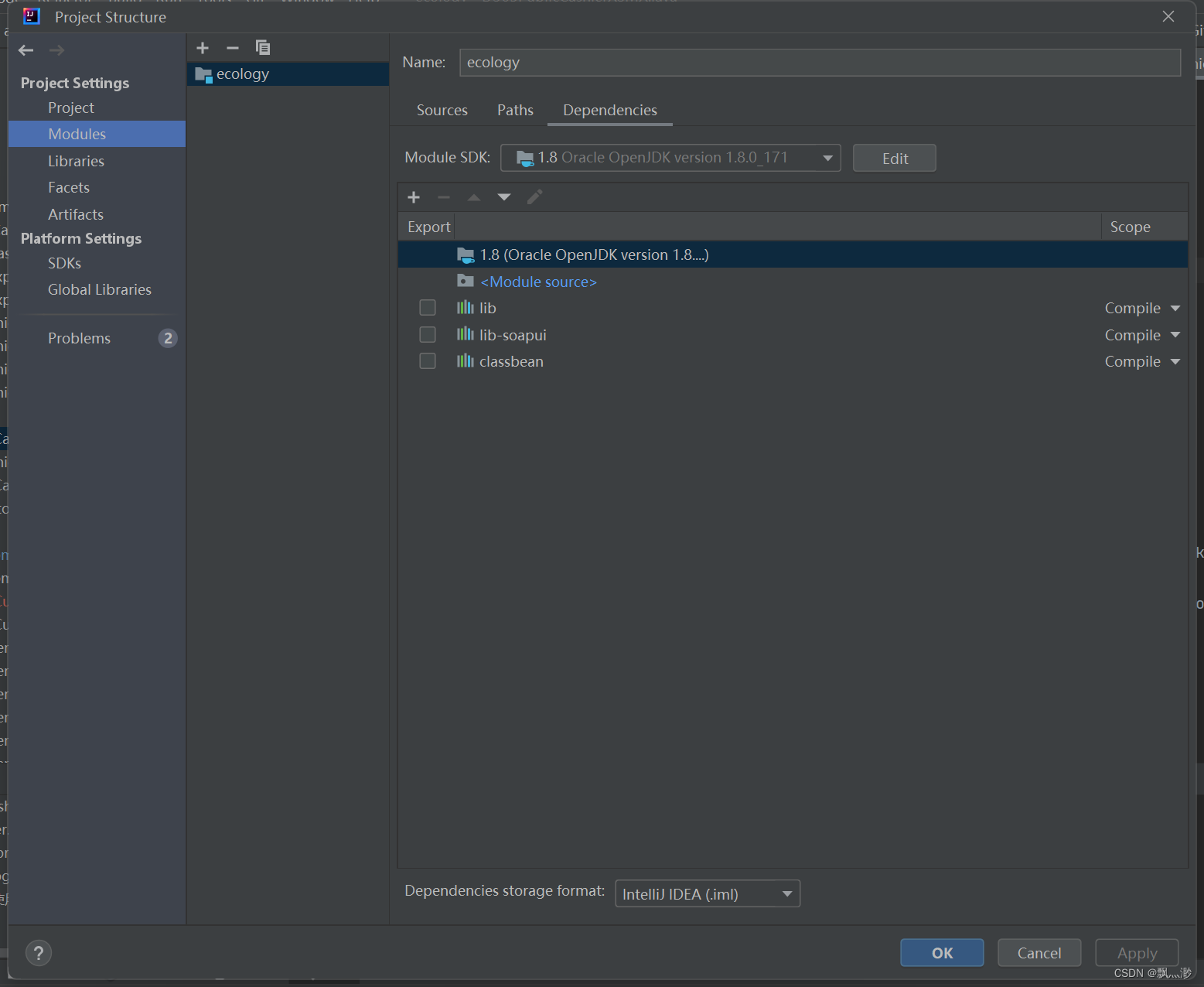
IDEA 编译单个Java文件
文章目录 一、class文件的生成位置二、编译单个文件编译项目报错Error:java: 无效的源发行版: 8 一、class文件的生成位置 file->project structure->Modules 二、编译单个文件 选中文件,点击recompile 编译项目报错 Error:java: 无效的源发行版: 8 Fi…...

人工智能业务分析
人工智能业务分析的组成图 #mermaid-svg-SKV0WrbMSANzQz4U {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SKV0WrbMSANzQz4U .error-icon{fill:#552222;}#mermaid-svg-SKV0WrbMSANzQz4U .error-text{fill:#552222;s…...

随机文本生成器
目录 开头程序程序的流程图程序打印的效果(不必细看,因为字符太多)例1例2例3 结尾 开头 大家好,我叫这是我58。看!这下面有一个程序。 程序 #define _CRT_SECURE_NO_WARNINGS 1 #include <stdio.h> #include <random> #includ…...

java中输入输出流的继承关系
在 Java 中,输入输出流的继承关系主要围绕两个抽象基类展开:字节流基类 InputStream 和 OutputStream,以及字符流基类 Reader 和 Writer。这些类形成了 Java I/O 系统的基础,提供了丰富的子类以适应不同的输入输出需求。 字节流 字节流用于处理原始的二进制数据。 Input…...

c++应用网络编程之一基本介绍
一、网络编程介绍 c编程的应用场景在前面分析过,一个重要的方向就是网络编程。一般来说,开发者说的服务端编程在c方向上简单的可以认为是网络编程。首先需要说明的,本系列不对网络编程的相关基础知识展开详细的说明,因为这种知识…...

Web后端开发概述环境搭建项目创建servlet生命周期
Web开发概述 web开发指的就是网页向后再让发送请求,与后端程序进行交互 web后端(javaEE)程序需要运行在服务器中 这样前端才可以对其进行进行访问 什么是服务器? 解释1: 服务器就是一款软件,可以向其发送请求,服务器会做出一个响应.可以在服务器中部署文件,让…...

Java 位运算详解
位运算是一种直接在二进制位上进行操作的方式。位运算符包括按位与 (&)、按位或 (|)、按位异或 (^)、按位非 (~)、左移 (<<)、右移 (>>) 和无符号右移 (>>>)。这些操作符用于操作整型数据类型,如 int 和 long。 一、按位与 (&) 按位…...

智能体实战:开发一个集成国内AI平台的GPTs,自媒体高效智能助手
文章目录 一,什么是GPTs二,开发GPTs1,目标2,开发2.1 打开 GPTS:https://chat.openai.com/gpts2.2 点击 Create 创建一个自己的智能体 2.3 配置GPTs2.4 配置外挂工具2.4.1 配置Authentication-授权2.4.1.1 生成语聚AI的…...

完美世界|单机版合集(共22个版本)
前言 我是研究单机的老罗,今天给大家带来的是完美世界的单机版合集,一共22个版本。本人亲自测试了一个版本,运行视频如下: 完美世界|单机版合集 先看所有的版本的文件,文件比较大,准备好空间,差…...

Jenkins的一些记录
设置环境变量 在 Jenkins 流水线中,取决于使用的是声明式还是脚本式流水线,设置环境变量的方法不同。 声明式流水线支持 environment 指令,而脚本式流水线的使用者必须使用 withEnv 步骤。 pipeline {agent anyenvironment { CC clang}stag…...

讲讲js中的prototype和__proto__
在Javascript中,prototype和__proto__是两个重要的概念,在对象的原型链中扮演重要的角色。 prototype prototype是js函数的内置属性,每个函数都有一个prototype属性,它是一个指针,指向一个对象(原型对象&a…...
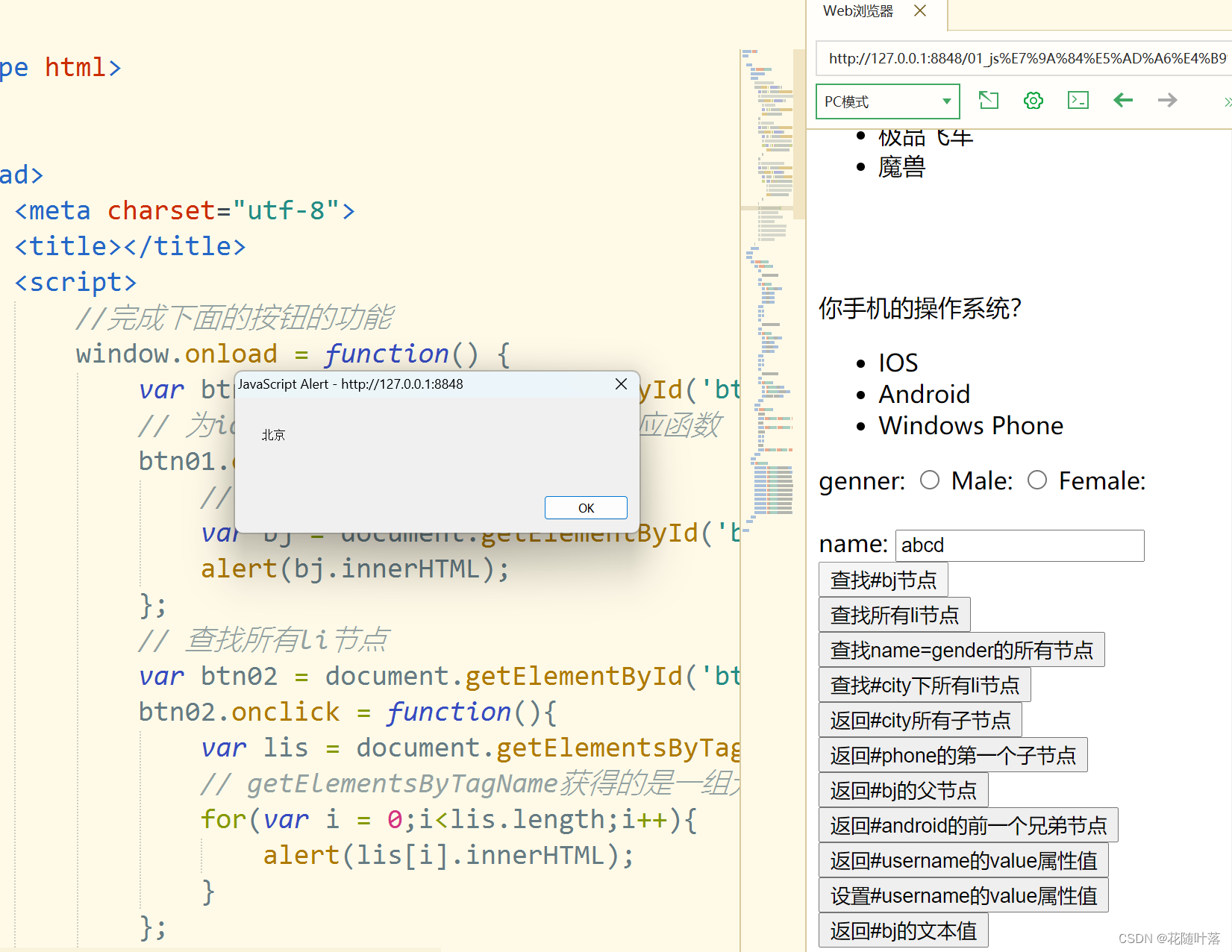
JavaScript的学习之DOM的查询(一)
一、获得元素 通过document对象调用: getElementById():通过id属性获取一个元素节点对象getElementsByTagName():通过标签名获取一组元素节点对象getElementsByName():通过name属性来获取一组元素节点对象 核心学习代码 <scrip…...
充电宝哪个品牌比较好一点?多维度实测西圣、绿联、倍思充电宝!
在这个快节奏的时代,智能手机已成为我们日常生活不可或缺的一部分,而充电宝作为其能量补给站,重要性不言而喻。面对市场上琳琅满目的充电宝品牌与型号,如何挑选一款既实用又高效的充电伴侣,成为了许多消费者的难题。今…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
