代码随想录-Day44
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0

class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//当金额为0时需要的硬币数目为0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}
}
这段Java代码实现了一个经典的动态规划问题——“完全背包问题”的一个应用场景:给定不同面额的硬币coins和一个总金额amount,计算最少需要多少个硬币凑出这个金额,如果不可能凑出则返回-1。这里是使用完全背包的思路,即每种硬币可以无限使用。
代码解析:
-
初始化:首先,定义一个
dp数组,长度为amount + 1,并将其所有值初始化为Integer.MAX_VALUE,表示在没有计算之前,达到每个金额所需的最小硬币数为正无穷大。例外的是,dp[0]初始化为0,因为当金额为0时,不需要任何硬币。 -
双重循环:
- 外层循环遍历硬币数组
coins,即遍历每一种硬币面额。 - 内层循环从当前硬币的面额
coins[i]开始遍历到总金额amount。这是因为在遍历到的金额j上,只有当j至少为当前硬币面额时,才有可能使用当前硬币去构成这个金额。
- 外层循环遍历硬币数组
-
状态转移方程:对于内层循环中的每个
j,如果dp[j - coins[i]]不是初始的最大值(即存在一种方式可以构成j - coins[i]的金额),则考虑使用一个面额为coins[i]的硬币,更新dp[j]为dp[j]和dp[j - coins[i]] + 1中的较小值。这里dp[j - coins[i]] + 1表示在构成j - coins[i]的基础上再加一个面额为coins[i]的硬币。 -
返回结果:最后,检查
dp[amount]是否仍为Integer.MAX_VALUE,如果是,则说明没有找到任何组合可以凑成总金额,返回-1;否则返回dp[amount],即最少需要的硬币数。
总结:
这段代码通过动态规划的完全背包方法,有效解决了最少硬币数量问题,时间复杂度为O(coins.length * amount),空间复杂度为O(amount)。
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9

方法一:
class Solution {// 版本一,先遍历物品, 再遍历背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//当和为0时,组合的个数为0dp[0] = 0;// 遍历物品for (int i = 1; i * i <= n; i++) {// 遍历背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}
这段Java代码是解决完全平方数问题的一个动态规划实现,目标是找出最少数量的完全平方数(例如1, 4, 9, 16…)之和,使其等于给定的正整数n。代码采用了“先遍历物品,再遍历背包”的动态规划策略,这里的“物品”指的是完全平方数,而“背包”则是我们需要达到的目标和n。
代码解析
-
初始化dp数组:首先,创建一个长度为
n+1的数组dp,其中dp[j]表示和为j时所需的最少完全平方数的个数。初始化所有dp[j]为Integer.MAX_VALUE,表示初始时没有找到任何组合。但因为任何正整数都可以由无数个1^2组成,所以实际上不需要初始化为Integer.MAX_VALUE,直接初始化为一个较大的数即可,或明确知道最小组合数为1(当j > 0时)。注释中提到的Arrays.fill(dp, Integer.MAX_VALUE);是一种更简洁的初始化方式,但在这个特定问题上下文里,初始化为极大值然后在特定条件下更新的逻辑是多余的。 -
初始化dp[0]:当和为0时,不需要任何完全平方数,所以
dp[0]设置为0。 -
双重循环:
- 外层循环遍历所有可能的完全平方数(由
1^2到√n的平方),用i表示当前考虑的完全平方数的根。 - 内层循环遍历从当前完全平方数
i*i开始到目标和n的所有可能和j。对于每个j,如果可以通过添加当前完全平方数i*i使得总和不超过n,并且这样的操作能减少之前记录的最少完全平方数的个数,就更新dp[j]的值为dp[j - i * i] + 1。
- 外层循环遍历所有可能的完全平方数(由
-
返回结果:最后返回
dp[n],即和为n时所需的最少完全平方数的个数。
注意
- 代码注释中指出的“不需要这个if statement”,是因为在找完全平方数之和的问题中,任何正整数
n都可以通过至少一个1^2(即至少一个1)来组合得到,所以直接尝试更新dp[j]的值而不需检查之前是否达到过是不可能的状态(即dp[j - i * i] != max的检查没有必要)。
综上,这段代码通过动态规划方法有效地求解了最少完全平方数之和的问题。
方法二:
class Solution {// 版本二, 先遍历背包, 再遍历物品public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];// 初始化for (int j = 0; j <= n; j++) {dp[j] = max;}// 当和为0时,组合的个数为0dp[0] = 0;// 遍历背包for (int j = 1; j <= n; j++) {// 遍历物品for (int i = 1; i * i <= j; i++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}
这段Java代码是解决“完全平方数”的另一个动态规划实现版本,目标依然是找出最少数量的完全平方数(如1, 4, 9, 16…)之和,使得这个和等于给定的正整数n。与第一个版本的主要区别在于遍历的顺序:这里是“先遍历背包,再遍历物品”。
代码解析
-
初始化:与第一个版本相同,首先创建一个长度为
n+1的数组dp,其中dp[j]表示和为j时所需的最少完全平方数的个数。初始化所有dp[j]为Integer.MAX_VALUE,然后设置dp[0]=0,表示和为0时不需要任何完全平方数。 -
遍历顺序改变:
- 外层循环现在遍历背包容量(从1到
n),用j表示当前考虑的总和。 - 内层循环遍历所有可能的完全平方数(从
1^2到刚好不超过当前总和j的完全平方数),用i表示当前完全平方数的根。这确保了每次内循环都是对一个有效的完全平方数进行操作,不会超出背包容量。
- 外层循环现在遍历背包容量(从1到
-
状态转移:对于每个背包容量
j,遍历所有小于等于它的完全平方数i*i,并尝试将当前完全平方数加入组合中(即从dp[j - i * i]转移而来),然后通过Math.min()函数更新dp[j]为已知的最小组合数。 -
返回结果:最后返回
dp[n],即和为n时,所需最少的完全平方数个数。
优缺点
- 优点:这种“先遍历背包,再遍历物品”的方式直接反映了背包问题的经典解法,逻辑上清晰地表达了对于每个总和
j,尝试用所有可能的完全平方数去填充它,寻找最小组合数。 - 缺点:在这个特定问题上,两种遍历顺序(先物品后背包 vs. 先背包后物品)在逻辑复杂度和效率上并无本质区别,主要取决于个人理解偏好。实际上,由于完全平方数的特殊性(连续的完全平方数之间差距增大),遍历顺序对性能的影响相对较小。
总之,这个版本提供了解决“完全平方数”问题的另一种动态规划实现思路,关键在于遍历顺序的调整,但核心的动态规划思想和状态转移方程保持一致。
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
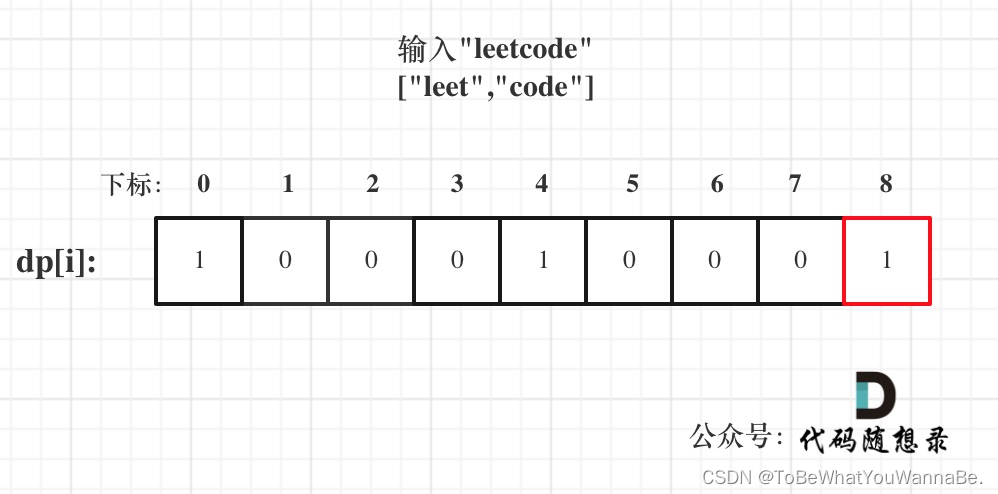
方法一:
class Solution {public boolean wordBreak(String s, List<String> wordDict) {HashSet<String> set = new HashSet<>(wordDict);boolean[] valid = new boolean[s.length() + 1];valid[0] = true;for (int i = 1; i <= s.length(); i++) {for (int j = 0; j < i && !valid[i]; j++) {if (set.contains(s.substring(j, i)) && valid[j]) {valid[i] = true;}}}return valid[s.length()];}
}
这段Java代码是一个解决方案,用于解决“单词拆分”问题。给定一个字符串s和一个字典wordDict(单词列表),判断字符串s是否可以被空格拆分成一个或多个字典中的单词。这是一个典型的动态规划问题。
代码解析
-
数据结构转换:首先,将
wordDict转换为哈希集合HashSet<String> set,这样可以以O(1)的时间复杂度查询一个字符串是否在字典中。 -
初始化:定义一个布尔型数组
valid,长度为s.length() + 1,其中valid[i]表示字符串s的前i个字符组成的子串是否可以被拆分成字典中的单词。初始化valid[0]为true,因为空字符串是可以“拆分”的。 -
动态规划填充:外层循环从1遍历到
s.length(),代表当前正在检查的子串的结束位置。内层循环从0遍历到当前的结束位置i,这是为了找到所有可能的前缀子串。如果存在某个前缀子串(从索引j到i)在字典集合中,并且这个前缀子串的前一个位置(即j)的子串也是合法的(valid[j]为true),那么将当前位置i标记为合法(valid[i] = true)。这里使用了!valid[i]作为提前终止的条件,一旦找到一个合法的拆分方式就不再继续查找,提高了效率。 -
返回结果:最后返回
valid[s.length()],即整个字符串s是否可以被成功拆分。
示例
假设s = "leetcode",wordDict = ["leet", "code"],该函数将返回true,因为可以将s拆分成"leet"和"code",这两个单词都在字典中。
这段代码通过动态规划有效地解决了单词拆分问题,具有较好的时间和空间效率。
方法二:
// 另一种思路的背包算法
class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] dp = new boolean[s.length() + 1];dp[0] = true;for (int i = 1; i <= s.length(); i++) {for (String word : wordDict) {int len = word.length();if (i >= len && dp[i - len] && word.equals(s.substring(i - len, i))) {dp[i] = true;break;}}}return dp[s.length()];}
}
这段代码同样采用动态规划的思路来解决“单词拆分”问题,但实现方式稍有不同,具体解析如下:
算法思路
-
初始化:创建一个布尔型数组
dp,长度为s.length() + 1,其中dp[i]表示字符串s的前i个字符组成的子串是否能被字典中的单词组合覆盖。初始化dp[0] = true,表示空字符串是可以被任何词典中的单词组合覆盖的。 -
双重循环遍历:
- 外层循环从1遍历到
s.length(),用i表示当前考虑的子串的结束位置。 - 内层循环遍历字典
wordDict中的每个单词word。- 计算当前单词的长度
len。 - 判断当前子串的起始位置是否允许截取长度为
len的子串,即i >= len,同时检查前len个字符组成的子串(即s.substring(i - len, i))是否与当前单词相等,并且这个子串的前一个位置的子串是否能被词典中的单词组合覆盖(即dp[i - len]为true)。 - 如果上述条件满足,说明找到了一个匹配的单词,可以将当前位置
i标记为true并跳出内层循环,因为一旦找到一个合法的拆分方式就没有必要继续检查当前i的其他单词了(利用了“一旦满足条件即可结束”的剪枝优化)。
- 计算当前单词的长度
- 外层循环从1遍历到
-
返回结果:最后返回
dp[s.length()],表示整个字符串s是否可以被字典中的单词组合覆盖。
优势与特点
- 剪枝优化:通过在找到符合条件的单词后立即中断内层循环,减少了不必要的循环次数,提高了算法效率。
- 直观易懂:代码直接体现了对每个子串尝试匹配字典中单词的过程,逻辑较为直观。
- 空间效率:此方法仅使用了一个长度等于字符串长度加一的布尔数组,空间复杂度为O(n),其中n为字符串
s的长度,与题目给定的字典大小无关,较为高效。
综上所述,这是一种有效且易于理解的动态规划解法,适用于解决给定字符串是否能被字典中的单词拆分的问题。
方法三:
// 回溯法+记忆化
class Solution {private Set<String> set;private int[] memo;public boolean wordBreak(String s, List<String> wordDict) {memo = new int[s.length()];set = new HashSet<>(wordDict);return backtracking(s, 0);}public boolean backtracking(String s, int startIndex) {// System.out.println(startIndex);if (startIndex == s.length()) {return true;}if (memo[startIndex] == -1) {return false;}for (int i = startIndex; i < s.length(); i++) {String sub = s.substring(startIndex, i + 1);// 拆分出来的单词无法匹配if (!set.contains(sub)) {continue; }boolean res = backtracking(s, i + 1);if (res) return true;}// 这里是关键,找遍了startIndex~s.length()也没能完全匹配,标记从startIndex开始不能找到memo[startIndex] = -1;return false;}
}
这段代码提供了一个使用回溯法加记忆化的解决方案来解决“单词拆分”问题。给定一个字符串s和一个单词字典wordDict,判断字符串s是否可以被空格拆分成一个或多个字典中的单词。以下是代码的详细解析:
类成员变量
- set: 存储字典
wordDict中的所有单词,使用HashSet以支持快速查找。 - memo: 记忆化数组,用于存储字符串
s的各个起始位置是否能够被拆分成字典中的单词。初始化为整型数组,长度与s相同,初始值默认为0,-1表示从该位置开始的子串不能被拆分。
方法解析
wordBreak 方法
- 初始化
memo数组和set集合。 - 调用
backtracking方法,从字符串的起始位置开始尝试拆分。
backtracking 方法
-
参数:
s: 输入字符串。startIndex: 当前开始拆分的位置索引。
-
目的:
- 递归地尝试从
startIndex开始的子串是否能被拆分成字典中的单词。
- 递归地尝试从
-
逻辑:
- 基础情况:如果
startIndex等于字符串长度,说明已经成功拆分到末尾,返回true。 - 记忆化检查:如果
memo[startIndex]为-1,说明从startIndex开始的子串已经被探索过且不可拆分,直接返回false。 - 遍历:从
startIndex到字符串结尾,逐步尝试截取子串,并检查该子串是否在字典中。- 如果子串在字典中,递归调用
backtracking(s, i + 1),尝试剩余部分能否拆分。 - 如果剩余部分可以被拆分,则当前子串也能被拆分,返回
true。
- 如果子串在字典中,递归调用
- 回溯:如果所有尝试都无法成功拆分,标记
memo[startIndex] = -1,表示从这个位置开始的子串不能被拆分,然后返回false。
- 基础情况:如果
关键点
- 记忆化搜索:通过
memo数组避免重复计算,提高效率。 - 回溯:在尝试失败后记录失败信息,防止同一子问题的重复探索。
这种方法在处理较长字符串和较大字典时,相较于简单的递归或暴力搜索能显著提升效率,但消耗的空间也会相应增加,主要是由于记忆化数组的使用。
相关文章:

代码随想录-Day44
322. 零钱兑换 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数…...
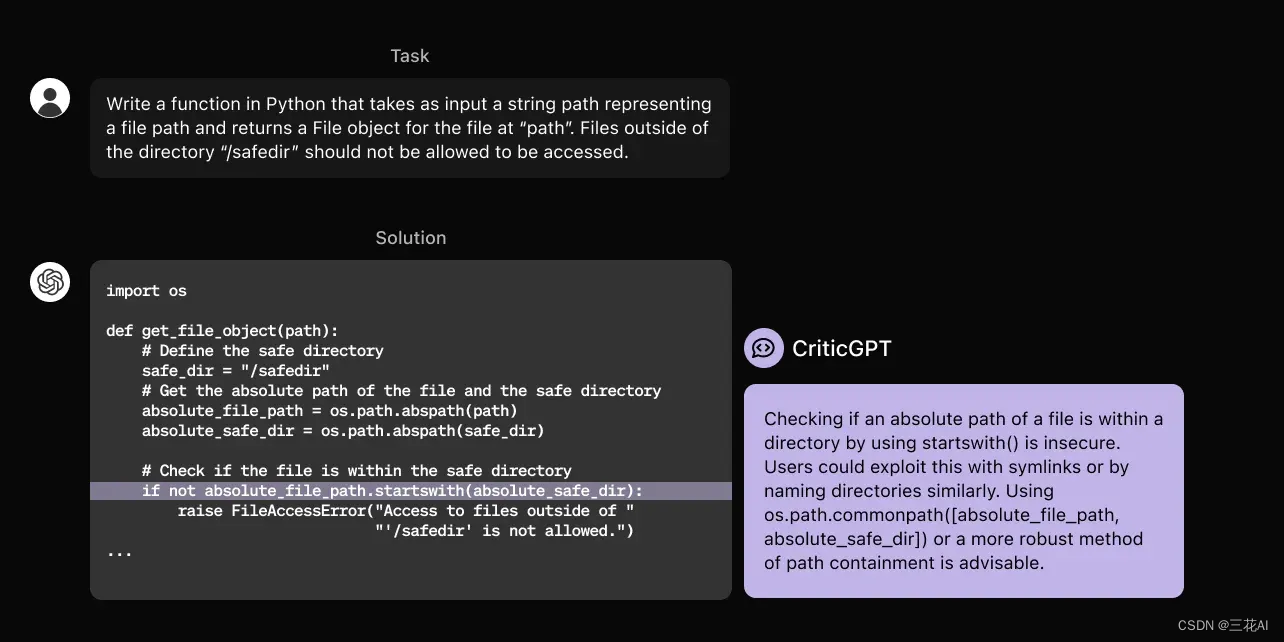
CriticGPT: 用 GPT-4 找出 GPT-4 的错误
CriticGPT 是 OpenAI 发布的一个基于 GPT-4 的模型,它可以帮助我们人类 Review 并纠正 ChatGPT 在生成代码时的错误。使用 CriticGPT 审查代码时,有 60% 的概率生成的代码更好更正确。...

SpringBoot:SpringBoot中调用失败如何重试
一、引言 在实际的应用中,我们经常需要调用第三方API来获取数据或执行某些操作。然而,由于网络不稳定、第三方服务异常等原因,API调用可能会失败。为了提高系统的稳定性和可靠性,我们通常会考虑实现重试机制。 Spring Retry为Spri…...

2024-06-24 问AI: 在大语言模型中,什么是ray?
文心一言 在大语言模型中,Ray是一个开源的统一框架,用于扩展AI和Python应用程序,特别是在机器学习领域。以下是关于Ray的详细解释: 核心功能: Ray为并行处理提供了计算层,使得用户无需成为分布式系统专家…...

仓库管理系统09--修改用户密码
1、添加窗体 2、窗体布局控件 UI设计这块还是传统的表格布局,采用5行2列 3、创建viewmodel 4、前台UI绑定viewmodel 这里要注意属性绑定和命令绑定及命令绑定时传递的参数 <Window x:Class"West.StoreMgr.Windows.EditPasswordWindow"xmlns"http…...

在Spring Data JPA中使用@Query注解
目录 前言示例简单示例只查询部分字段,映射到一个实体类中只查询部分字段时,也可以使用List<Object[]>接收返回值再复杂一些 前言 在以往写过几篇spring data jpa相关的文章,分别是 Spring Data JPA 使用JpaSpecificationExecutor实现…...
【UE5.1】Chaos物理系统基础——01 创建可被破坏的物体
目录 步骤 一、通过笔刷创建静态网格体 二、破裂静态网格体 三、“统一” 多层级破裂 四、“簇” 群集化的破裂 五、几何体集的材质 六、防止几何体集自动破碎 步骤 一、通过笔刷创建静态网格体 1. 可以在Quixel Bridge中下载两个纹理,用于表示石块的内外纹…...

Linux下SUID提权学习 - 从原理到使用
目录 1. 文件权限介绍1.1 suid权限1.2 sgid权限1.3 sticky权限 2. SUID权限3. 设置SUID权限4. SUID提权原理5. SUID提权步骤6. 常用指令的提权方法6.1 nmap6.2 find6.3 vim6.4 bash6.5 less6.6 more6.7 其他命令的提权方法 1. 文件权限介绍 linux的文件有普通权限和特殊权限&a…...

Redis主从复制搭建一主多从
1、创建/myredis文件夹 2、复制redis.conf配置文件到新建的文件夹中 3、配置一主两从,创建三个配置文件 ----redis6379.conf ----redis6380.conf ----redis6381.conf 4、在三个配置文件写入内容 redis6379.conf里面的内容 include /myredis/redis.conf pidfile /va…...
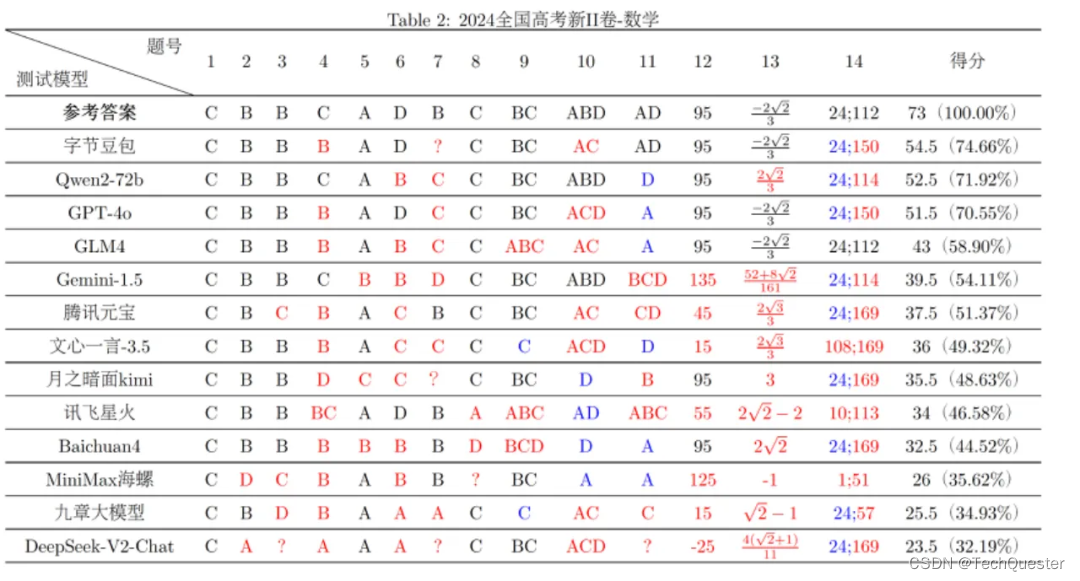
GPT-4o文科成绩超一本线,理科为何表现不佳?
目录 01 评测榜单 02 实际效果 什么?许多大模型的文科成绩竟然超过了一本线,还是在竞争激烈的河南省? 没错,最近有一项大模型“高考大摸底”评测引起了广泛关注。 河南高考文科今年的一本线是521分,根据这项评测&…...

Lombok的hashCode方法
Lombok对于重写hashCode的算法真的是很经典,但是目前而言有一个令人难以注意到的细节。在继承关系中,父类的hashCode针对父类的所有属性进行运算,而子类的hashCode却只是针对子类才有的属性进行运算,立此贴提醒自己。 目前重写ha…...

关于springboot创建kafkaTopic
工具类提供,方法名见名知意。使用kafka admin import org.apache.kafka.clients.admin.*; import org.apache.kafka.common.KafkaFuture;import java.util.*; import java.util.concurrent.ExecutionException;import org.apache.kafka.clients.admin.AdminClient; …...

OOAD的概念
面向对象分析与设计(OOAD, Object-Oriented Analysis and Design)是一种软件开发方法,它利用面向对象的概念和技术来分析和设计软件系统。OOAD 主要关注对象、类以及它们之间的关系,通过抽象、封装、继承和多态等面向对象的基本原…...

Day47
Day47 手写Spring-MVC之DispatcherServlet DispatcherServlet的思路: 前端传来URI,在TypeContainer容器类中通过uri得到对应的类描述类对象(注意:在监听器封装类描述类对象的时候,是针对于每一个URI进行封装的&#x…...

【面试系列】后端开发工程师 高频面试题及详细解答
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、…...

mac|浏览器链接不上服务器但可以登微信
千万千万千万不要没有关梯子直接关机,不然就会这样子呜呜呜 设置-网络,点击三个点--选择--位置--编辑位置(默认是自动) 新增一个,然后选中点击完成 这样就可以正常上网了...
Spring Cloud Alibaba之负载均衡组件Ribbon
一、什么是负载均衡? (1)概念: 在基于微服务架构开发的系统里,为了能够提升系统应对高并发的能力,开发人员通常会把具有相同业务功能的模块同时部署到多台的服务器中,并把访问业务功能的请求均…...
tkinter显示图片
tkinter显示图片 效果代码解析打开和显示图像 代码 效果 代码解析 打开和显示图像 def open_image():file_path filedialog.askopenfilename(title"选择图片", filetypes(("PNG文件", "*.png"), ("JPEG文件", "*.jpg;*.jpeg&q…...

000.二分查找算法题解目录
000.二分查找算法题解目录 69. x 的平方根(简单)34. 在排序数组中查找元素的第一个和最后一个位置(中等)...

数据资产赋能企业决策:通过精准的数据分析和洞察,构建高效的数据资产解决方案,为企业提供决策支持,助力企业实现精准营销、风险管理、产品创新等目标,提升企业竞争力
一、引言 在信息化和数字化飞速发展的今天,数据已成为企业最宝贵的资产之一。数据资产不仅包含了企业的基本信息,还蕴含了丰富的市场趋势、消费者行为和潜在商机。如何通过精准的数据分析和洞察,构建高效的数据资产解决方案,为企…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
