[信号与系统]IIR滤波器与FIR滤波器相位延迟定量的推导。
IIR滤波器与FIR滤波器最大的不同:相位延迟
IIR滤波器相位延迟分析
相位响应和延迟
这里讨论一下理想延迟系统的相位延迟。
对于一个给定的系统频率响应 H ( e j w ) H(e^{jw}) H(ejw)可以表示为
H ( e j w ) = ∣ H ( e j w ) ∣ e Φ ( w ) H(e^{jw}) = |H(e^{jw})|e^{Φ(w)} H(ejw)=∣H(ejw)∣eΦ(w)
其中 H ( e j w ) H(e^{jw}) H(ejw)是幅度响应, Φ ( w ) Φ(w) Φ(w)是相位响应。
延迟系统的相位响应
对于一个理想的延迟系统,其输出信号是输入信号的延迟版本,即:
y ( n ) = x ( n − τ ) y(n) = x(n-\tau) y(n)=x(n−τ)
其中 τ \tau τ是延迟时间,对应的频率响应为 H ( e j w ) = e − j w τ H(e^{jw})=e^{-jw\tau} H(ejw)=e−jwτ
这是因为延迟 τ \tau τ样本在时域上相当于在频域上乘以 e − j w τ e^{-jw\tau} e−jwτ
傅里叶变换和频域描述
为了理解延迟系统的频率响应,需要用到离散时间傅里叶变换(DTFT)。DTFT将时域信号转换为频域信号。
- 输入信号 x ( n ) x(n) x(n)的DTFT为:
X ( e j w ) = ∑ n = − ∞ ∞ x ( n ) e − j w n X(e^{jw}) = \sum_{n=-\infty}^{\infty} x(n) e^{-jwn} X(ejw)=n=−∞∑∞x(n)e−jwn
- 输出信号 y ( n ) y(n) y(n)的DTFT为:
Y ( e j w ) = ∑ n = − ∞ ∞ y ( n ) e − j w n Y(e^{jw}) = \sum_{n=-\infty}^{\infty} y(n) e^{-jwn} Y(ejw)=n=−∞∑∞y(n)e−jwn
延迟的影响
根据延迟系统的定义:
y ( n ) = x ( n − τ ) y(n) = x(n - \tau) y(n)=x(n−τ)
将这个关系代入到 y ( n ) y(n) y(n)的DTFT公式中:
Y ( e j w ) = ∑ n = − ∞ ∞ x ( n − τ ) e − j w n Y(e^{jw}) = \sum_{n=-\infty}^{\infty} x(n - \tau) e^{-jwn} Y(ejw)=n=−∞∑∞x(n−τ)e−jwn
可以通过变量替换来简化计算。令 k = n − τ k = n - \tau k=n−τ,则 n = k + τ n = k + \tau n=k+τ:
Y ( e j w ) = ∑ k = − ∞ ∞ x ( k ) e − j w ( k + τ ) Y(e^{jw}) = \sum_{k=-\infty}^{\infty} x(k) e^{-jw(k + \tau)} Y(ejw)=k=−∞∑∞x(k)e−jw(k+τ)
分离指数部分:
Y ( e j w ) = ∑ k = − ∞ ∞ x ( k ) e − j w k e − j w τ Y(e^{jw}) = \sum_{k=-\infty}^{\infty} x(k) e^{-jwk} e^{-jw\tau} Y(ejw)=k=−∞∑∞x(k)e−jwke−jwτ
注意到:
∑ k = − ∞ ∞ x ( k ) e − j w k = X ( e j w ) \sum_{k=-\infty}^{\infty} x(k) e^{-jwk} = X(e^{jw}) k=−∞∑∞x(k)e−jwk=X(ejw)
所以:
Y ( e j w ) = X ( e j w ) ⋅ e − j w τ Y(e^{jw}) = X(e^{jw}) \cdot e^{-jw\tau} Y(ejw)=X(ejw)⋅e−jwτ
频率响应
系统的频率响应 H ( e j w ) H(e^{jw}) H(ejw)定义为输出频域表示与输入频域表示的比值:
H ( e j w ) = Y ( e j w ) X ( e j w ) H(e^{jw}) = \frac{Y(e^{jw})}{X(e^{jw})} H(ejw)=X(ejw)Y(ejw)
将上面的结果代入:
H ( e j w ) = e − j w τ H(e^{jw}) = e^{-jw\tau} H(ejw)=e−jwτ
相位响应的推导
我们可以从延迟系统的频率响应H(e^jw)推导出其相位响应:
H ( e j w ) = e − j w τ H(e^{jw})=e^{-jw\tau} H(ejw)=e−jwτ
从上述式子可以看到,频率响应的相位部分为 Φ ( w ) = − w τ Φ(w)=-w\tau Φ(w)=−wτ
至此我们知道了系统的延迟是如何表达和推导的,那么我们现在来说一下为什么IIR滤波器和FIR滤波器在相位延迟上会有这么大差别。
IIR滤波器相位延迟分析
考虑一个IIR滤波器的频率响应函数,应当如下:
一般来说,一个IIR滤波器的输出可以表示为:
y ( n ) = ∑ k = 0 N b k x ( n − k ) − ∑ k = 1 M a k y ( n − k ) y(n) = \sum_{k=0}^{N} b_k x(n-k) - \sum_{k=1}^{M} a_k y(n-k) y(n)=k=0∑Nbkx(n−k)−k=1∑Maky(n−k)
其中, b k b_k bk和 a k a_k ak是滤波器的系数。
IIR滤波器的频率响应 H ( e j ω ) H(e^{j\omega}) H(ejω)通常表示为:
H ( e j ω ) = B ( e j ω ) A ( e j ω ) H(e^{j\omega}) = \frac{B(e^{j\omega})}{A(e^{j\omega})} H(ejω)=A(ejω)B(ejω)
其中, B ( e j ω ) B(e^{j\omega}) B(ejω)和 A ( e j ω ) A(e^{j\omega}) A(ejω)分别是分子和分母多项式:
B ( e j ω ) = ∑ k = 0 N b k e − j ω k B(e^{j\omega}) = \sum_{k=0}^{N} b_k e^{-j\omega k} B(ejω)=k=0∑Nbke−jωk
A ( e j ω ) = 1 + ∑ k = 1 M a k e − j ω k A(e^{j\omega}) = 1 + \sum_{k=1}^{M} a_k e^{-j\omega k} A(ejω)=1+k=1∑Make−jωk
相位响应 ϕ ( ω ) \phi(\omega) ϕ(ω)是频率响应的相位部分:
H ( e j ω ) = ∣ H ( e j ω ) ∣ e j ϕ ( ω ) H(e^{j\omega}) = |H(e^{j\omega})| e^{j\phi(\omega)} H(ejω)=∣H(ejω)∣ejϕ(ω)
ϕ ( ω ) = arg ( H ( e j ω ) ) \phi(\omega) = \arg(H(e^{j\omega})) ϕ(ω)=arg(H(ejω))
为了定量地分析IIR滤波器的延迟,我们需要计算相位响应的频率导数,即群延迟 τ g ( ω ) \tau_g(\omega) τg(ω):
τ g ( ω ) = − d ϕ ( ω ) d ω \tau_g(\omega) = -\frac{d\phi(\omega)}{d\omega} τg(ω)=−dωdϕ(ω)
由于IIR滤波器的相位响应不是线性的,所以其群延迟通常是频率的函数,即延迟是频率依赖的。
定量推导(纯数学计算)
我们以一个简单的一阶IIR滤波器为例,分析其延迟特性。考虑一个一阶IIR滤波器,其差分方程为:
y ( n ) = x ( n ) − a y ( n − 1 ) y(n) = x(n) - a y(n-1) y(n)=x(n)−ay(n−1)
其频率响应为:
H ( e j ω ) = 1 1 − a e − j ω H(e^{j\omega}) = \frac{1}{1 - a e^{-j\omega}} H(ejω)=1−ae−jω1
- 计算频率响应的相位:
H ( e j ω ) = 1 1 − a e − j ω H(e^{j\omega}) = \frac{1}{1 - a e^{-j\omega}} H(ejω)=1−ae−jω1
我们将其写成极坐标形式:
H ( e j ω ) = 1 1 − 2 a cos ( ω ) + a 2 e j ϕ ( ω ) H(e^{j\omega}) = \frac{1}{\sqrt{1 - 2a\cos(\omega) + a^2}} e^{j\phi(\omega)} H(ejω)=1−2acos(ω)+a21ejϕ(ω)
其中,
ϕ ( ω ) = − tan − 1 ( a sin ( ω ) 1 − a cos ( ω ) ) \phi(\omega) = -\tan^{-1}\left(\frac{a \sin(\omega)}{1 - a \cos(\omega)}\right) ϕ(ω)=−tan−1(1−acos(ω)asin(ω))
- 计算群延迟:
τ g ( ω ) = − d ϕ ( ω ) d ω \tau_g(\omega) = -\frac{d\phi(\omega)}{d\omega} τg(ω)=−dωdϕ(ω)
ϕ ( ω ) = − tan − 1 ( a sin ( ω ) 1 − a cos ( ω ) ) \phi(\omega) = -\tan^{-1}\left(\frac{a \sin(\omega)}{1 - a \cos(\omega)}\right) ϕ(ω)=−tan−1(1−acos(ω)asin(ω))
利用导数链式法则,
τ g ( ω ) = − d d ω [ − tan − 1 ( a sin ( ω ) 1 − a cos ( ω ) ) ] \tau_g(\omega) = -\frac{d}{d\omega} \left[-\tan^{-1}\left(\frac{a \sin(\omega)}{1 - a \cos(\omega)}\right)\right] τg(ω)=−dωd[−tan−1(1−acos(ω)asin(ω))]
计算导数:
τ g ( ω ) = a ( 1 − a cos ( ω ) ) cos ( ω ) + a 2 sin 2 ( ω ) ( 1 − a cos ( ω ) ) 2 + a 2 sin 2 ( ω ) \tau_g(\omega) = \frac{a \left(1 - a \cos(\omega)\right)\cos(\omega) + a^2 \sin^2(\omega)}{\left(1 - a \cos(\omega)\right)^2 + a^2 \sin^2(\omega)} τg(ω)=(1−acos(ω))2+a2sin2(ω)a(1−acos(ω))cos(ω)+a2sin2(ω)
简化后得到:
τ g ( ω ) = a ( 1 − a cos ( ω ) + a cos 2 ( ω ) ) 1 − 2 a cos ( ω ) + a 2 \tau_g(\omega) = \frac{a \left(1 - a \cos(\omega) + a \cos^2(\omega)\right)}{1 - 2a \cos(\omega) + a^2} τg(ω)=1−2acos(ω)+a2a(1−acos(ω)+acos2(ω))
由于公式较为复杂,我们可以直接用数值方法计算和绘制IIR滤波器的群延迟特性。
举个例子
我们来搞个示例,这样好懂一点:
考虑一个简单的一阶滤波器
H ( e j w ) = 1 1 − a e − j w H(e^jw)=\frac{1}{1-ae^{-jw}} H(ejw)=1−ae−jw1
其相位响应为:
ϕ ( w ) = − a r g ( 1 − a e − j w ) ϕ(w)=-arg(1-ae^{-jw}) ϕ(w)=−arg(1−ae−jw)
我们可以看到,这个相位响应显然是非线性的,会随着w的不停变化,其变化率也会发生变化,说着说导数的比值会随着w的变化而变化,这显然是我们不想要看到的结果。
FIR滤波器相位延迟分析
FIR滤波器的相位延迟推导
FIR(有限脉冲响应)滤波器的延迟特性通常是线性的,这源于其非递归结构和对称系数设计。下面我们详细推导FIR滤波器的相位延迟,并展示如何利用KaTeX进行Markdown文档的编写。
FIR滤波器的基本形式
一个FIR滤波器的输出可以表示为:
y ( n ) = ∑ k = 0 N b k x ( n − k ) y(n) = \sum_{k=0}^{N} b_k x(n-k) y(n)=k=0∑Nbkx(n−k)
其中, b k b_k bk 是滤波器的系数, N N N 是滤波器的阶数。
频率响应和相位响应
FIR滤波器的频率响应 H ( e j ω ) H(e^{j\omega}) H(ejω) 可以表示为:
H ( e j ω ) = ∑ k = 0 N b k e − j ω k H(e^{j\omega}) = \sum_{k=0}^{N} b_k e^{-j\omega k} H(ejω)=k=0∑Nbke−jωk
相位响应 ϕ ( ω ) \phi(\omega) ϕ(ω) 是频率响应的相位部分:
H ( e j ω ) = ∣ H ( e j ω ) ∣ e j ϕ ( ω ) H(e^{j\omega}) = |H(e^{j\omega})| e^{j\phi(\omega)} H(ejω)=∣H(ejω)∣ejϕ(ω)
ϕ ( ω ) = arg ( H ( e j ω ) ) \phi(\omega) = \arg(H(e^{j\omega})) ϕ(ω)=arg(H(ejω))
线性相位的条件
为了实现线性相位,我们通常设计FIR滤波器的系数使其具有对称性或反对称性。对于一个长度为 N + 1 N+1 N+1 的对称FIR滤波器,其系数满足:
b k = b N − k b_k = b_{N-k} bk=bN−k
对于反对称FIR滤波器,其系数满足:
b k = − b N − k b_k = -b_{N-k} bk=−bN−k
这两种对称性保证了滤波器的相位响应是线性的,即:
ϕ ( ω ) = − ω τ \phi(\omega) = -\omega \tau ϕ(ω)=−ωτ
其中, τ \tau τ 是一个常数,表示恒定的群延迟。
定量推导
考虑一个对称的FIR滤波器,其冲激响应 h ( n ) h(n) h(n) 为:
h ( n ) = h ( N − 1 − n ) h(n) = h(N-1-n) h(n)=h(N−1−n)
其频率响应为:
H ( e j ω ) = ∑ k = 0 N − 1 h ( k ) e − j ω k H(e^{j\omega}) = \sum_{k=0}^{N-1} h(k) e^{-j\omega k} H(ejω)=k=0∑N−1h(k)e−jωk
由于 h ( n ) h(n) h(n) 的对称性,我们可以将其拆分并合并:
H ( e j ω ) = ∑ k = 0 ( N − 1 ) / 2 h ( k ) ( e − j ω k + e − j ω ( N − 1 − k ) ) H(e^{j\omega}) = \sum_{k=0}^{(N-1)/2} h(k) \left( e^{-j\omega k} + e^{-j\omega (N-1-k)} \right) H(ejω)=k=0∑(N−1)/2h(k)(e−jωk+e−jω(N−1−k))
利用欧拉公式,我们有:
e − j ω ( N − 1 − k ) = e − j ω ( N − 1 ) e j ω k e^{-j\omega (N-1-k)} = e^{-j\omega (N-1)} e^{j\omega k} e−jω(N−1−k)=e−jω(N−1)ejωk
合并后得到:
H ( e j ω ) = e − j ω ( N − 1 ) / 2 ∑ k = 0 ( N − 1 ) / 2 h ( k ) ( e − j ω ( k − ( N − 1 ) / 2 ) + e j ω ( k − ( N − 1 ) / 2 ) ) H(e^{j\omega}) = e^{-j\omega (N-1)/2} \sum_{k=0}^{(N-1)/2} h(k) \left( e^{-j\omega (k - (N-1)/2)} + e^{j\omega (k - (N-1)/2)} \right) H(ejω)=e−jω(N−1)/2k=0∑(N−1)/2h(k)(e−jω(k−(N−1)/2)+ejω(k−(N−1)/2))
这表明相位响应是线性的:
ϕ ( ω ) = − ω N − 1 2 \phi(\omega) = -\omega \frac{N-1}{2} ϕ(ω)=−ω2N−1
相关文章:

[信号与系统]IIR滤波器与FIR滤波器相位延迟定量的推导。
IIR滤波器与FIR滤波器最大的不同:相位延迟 IIR滤波器相位延迟分析 相位响应和延迟 这里讨论一下理想延迟系统的相位延迟。 对于一个给定的系统频率响应 H ( e j w ) H(e^{jw}) H(ejw)可以表示为 H ( e j w ) ∣ H ( e j w ) ∣ e Φ ( w ) H(e^{jw}) |H(e^{jw…...

Python海量数据处理脚本大集合:pyWhat
pyWhat:精简海联数据,直达数据弱点要害- 精选真开源,释放新价值。 概览 pyWhat是Github社区上一款比较实用的开源Python脚本工具。它能够快速提取信息中的 IP 地址、邮箱、信用卡、数字货币钱包地址、YouTube 视频等内容。当你遇到了一串莫名…...

postgresql搭建
搭建postgresql-11.3,和客户端工具 1,准备对应的包,右键直接下一步安装完即可, 将postgresql设置为本地服务,方便启动, 2,用对应客户端软件连接,新建一个数据库controlDB 新建用户…...

Web 品质标准
Web 品质标准 引言 随着互联网的快速发展,Web应用已经渗透到我们生活的方方面面。为了确保Web应用的质量,提高用户体验,Web品质标准应运而生。这些标准涵盖了多个方面,包括性能、安全性、可访问性、用户体验等。本文将详细介绍这些标准,并探讨它们在实际开发中的应用。 …...

深入理解PyTorch:原理与使用指南
文章目录 引言一、PyTorch的原理1. 动态计算图2. 自动微分3. 张量计算4. 高效的并行计算 二、PyTorch的使用1. 环境配置2. 加载数据3. 构建模型4. 训练模型5. 验证和测试模型 三、PyTorch的安装与配置四、PyTorch的使用示例总结 引言 在深度学习和机器学习的广阔领域中&#x…...
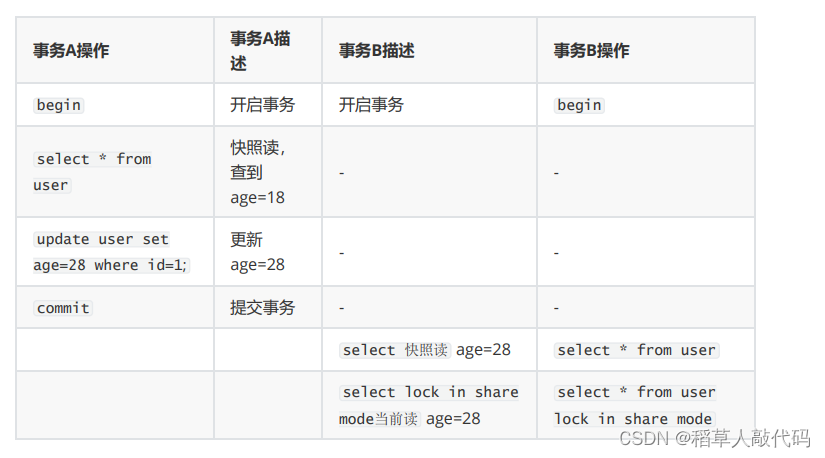
【MySQL事务】深刻理解事务隔离以及MVCC
文章目录 什么叫事务事务的提交方式常见的事务操作方式事务的开始与回滚总结 事务的隔离设置隔离级别解释脏读解释幻读解释不可重复读为什么可重复读不能解决幻读问题?总结 数据库并发的场景MVCC隐藏列字段undo日志Read view RR和RC的本质区别总结 什么叫事务 在My…...

关于Mac mini 10G网口的问题
问题: 购入一个10G网口的Mac mini M2,将其和自己的2.5G交换机连接,使用共享屏幕进行远程操作的过程中出现了频率极高的卡顿,几乎是几秒钟卡一下,使用ping进行测试发现卡的时候就ping不通了。测试使用Mac mini的无线网和雷电转2.5G…...

计算机网络-第4章 网络层
4.1网络层的几个重要概念 4.1.1网络层提供的两种服务 电信网面向连接通信方式,虚电路VC。 互联网设计思路:网络层要设计得尽量简单,向其上层只提供简单灵活的,尽最大努力交付的数据报服务。 网络层不提供服务质量的承诺&#…...

pytorch跑手写体实验
目录 1、环境条件 2、代码实现 3、总结 1、环境条件 pycharm编译器pytorch依赖matplotlib依赖numpy依赖等等 2、代码实现 import torch import torch.nn as nn import torch.optim as optim import torchvision import torchvision.transforms as transforms import matpl…...

利用Java的`java.util.concurrent`包优化多线程性能
利用Java的java.util.concurrent包优化多线程性能 一、引言 在Java的多线程编程中,性能优化是一个永恒的话题。随着多核CPU的普及和计算任务的日益复杂,多线程编程已经成为提高应用程序性能的重要手段。然而,多线程编程也带来了一系列的问题…...

软件著作权申请:开发者的重要保障与助力
一、引言 随着信息技术的飞速发展,软件产业已成为推动经济增长的重要动力。然而,在软件开发过程中,保护创作者的权益、防止抄袭和侵权行为显得尤为重要。软件著作权作为保护软件开发者权益的重要法律工具,其申请和登记流程对于软…...

WLAN Hostapd配置参数详解 - CN
想必大家平台在调试Hostapd时,针对某些特殊的参数,很难一下子理清楚其用法,这里对hostapd使用的配置参数进行一个归纳,以供大家参考( 其英文参考为:WLAN Hostapd配置参数详解 - EN-CSDN博客)&am…...

Excel 宏录制与VBA编程 ——VBA编程技巧篇一 (Union方法、Resize方法、Cells方法、UseSelect方法、With用法)
Uniom方法 使用Union方法可以将多个非连续区域连接起来成为一个区域,从而可以实现对多个非连续区域一起进行操作。 Resize方法 使用Range对象的Resize属性调整指定区域的大小,并返回调整大小后的单元格区域。 Cells方法 Cells属性返回一个Range对象。 Us…...
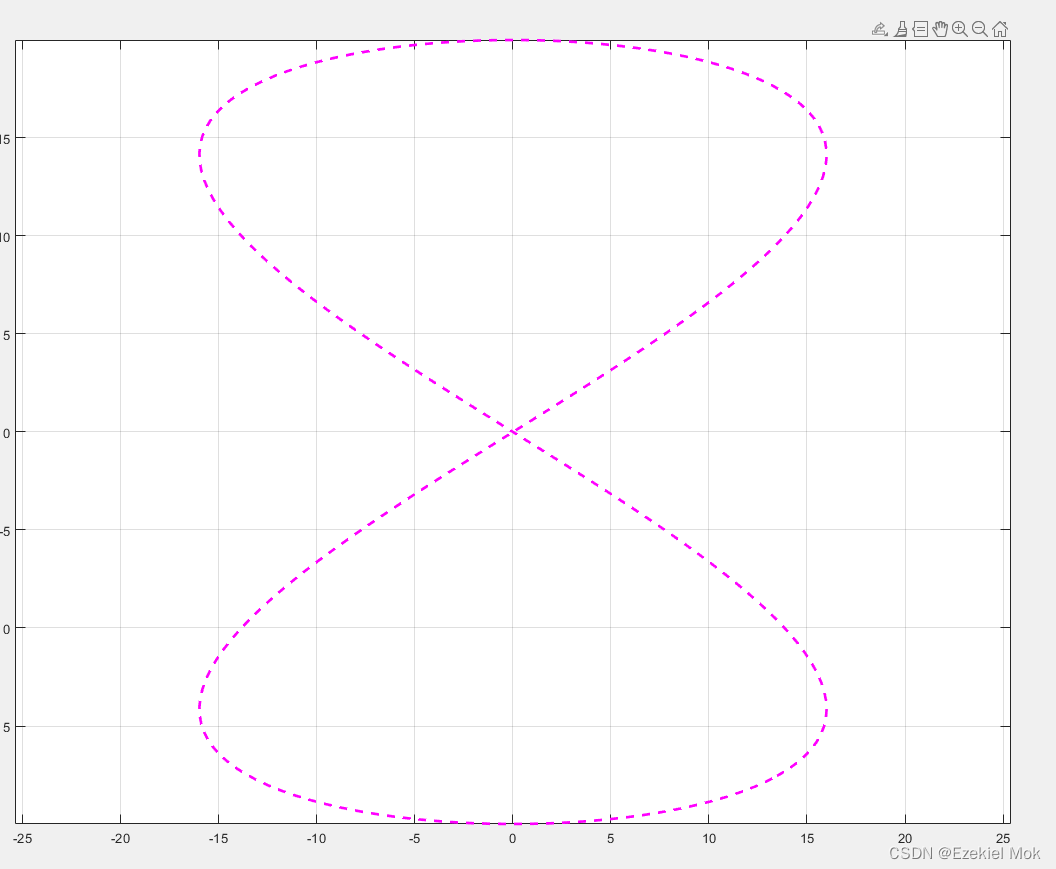
基于路径长度的样条插补算法(自动驾驶和路径跟踪控制适用)
以前在做车辆跟踪控制的时候发现在针对有多个X和多个Y对应的路径插补时候,总是报错,因为MATLAB里面的interp1插补函数它要求x要唯一对应一个y,当路径以单独的x或者y来求插补时候的时候就报错。由于在使用Matlab的interp1函数进行插值时&#…...
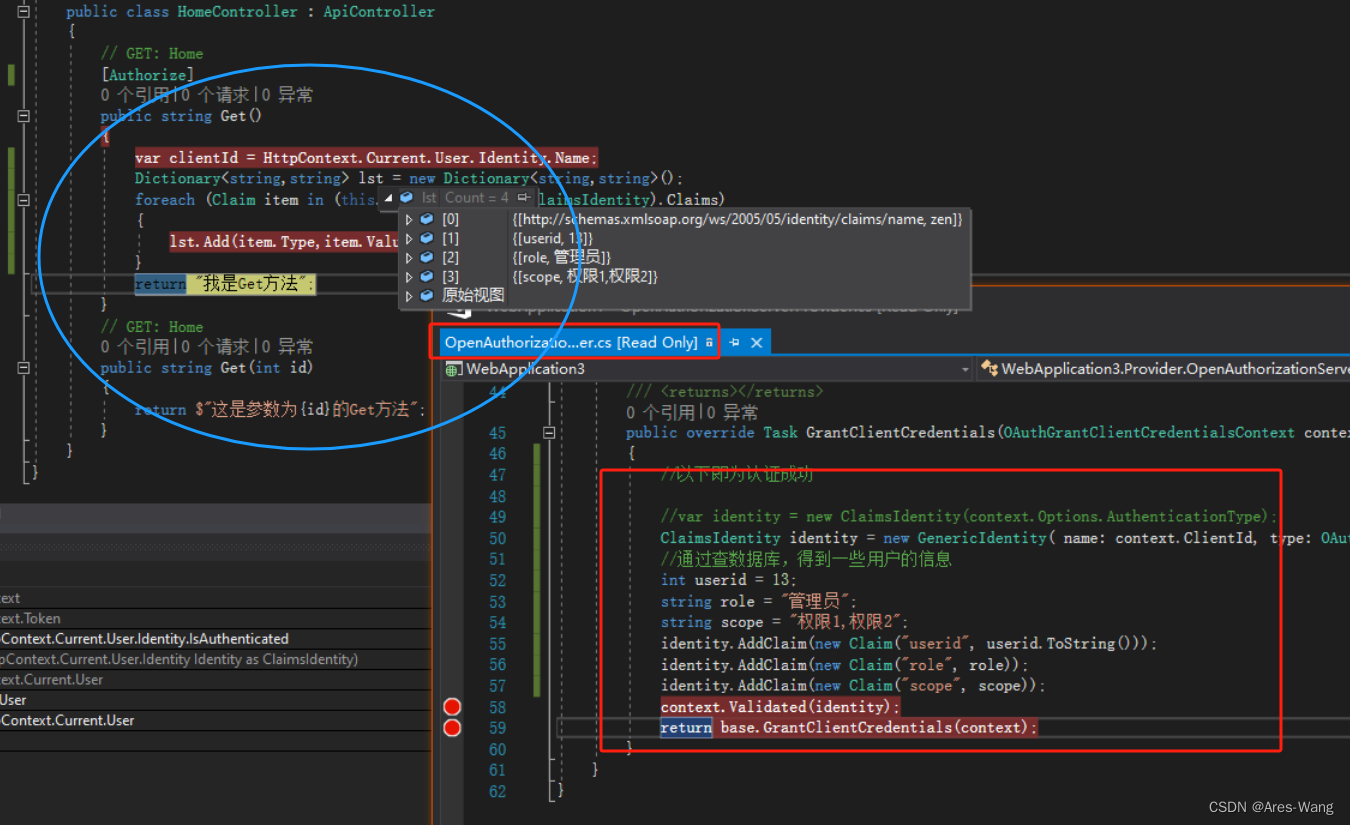
net Framework OAuth2.0
grant_type client_credentials 客户端凭证password 密码模式 用于资源所有者密码凭据token 隐藏式 、 简化式 简化模式又称为隐式授权码模式,它是授权码模式的一个简化版本authorization_code 授权码 A. 第三方程序向资源拥有者(用户)发送授权请求…...

速盾:服务器cdn加速超时如何解决?
CDN(Content Delivery Network,内容分发网络)是一种将网站内容分布到全球各地服务器上的技术,以提高网站的访问速度和用户体验。然而,在使用CDN时,有时候会遇到服务器CDN加速超时的问题,即CDN服…...
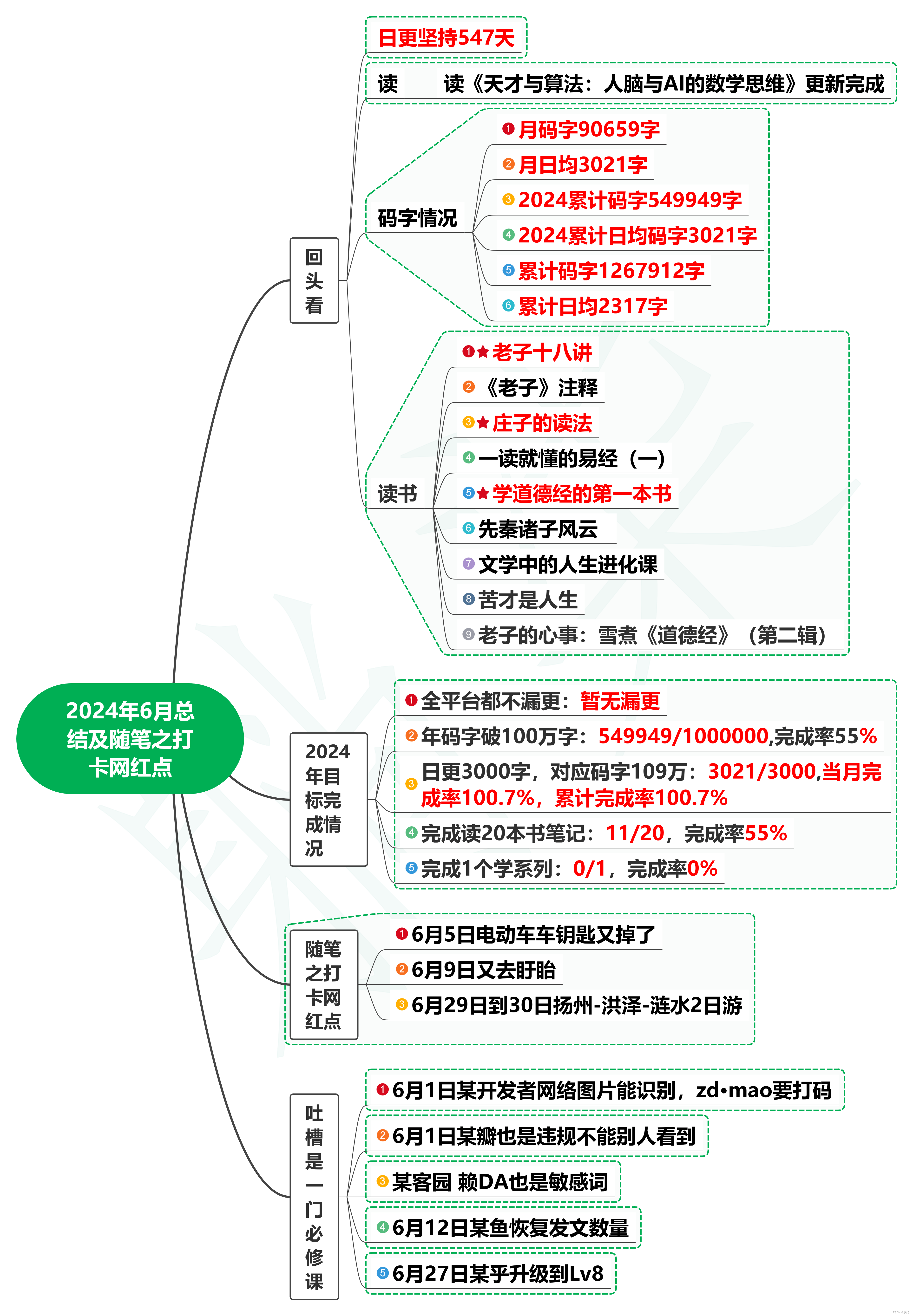
2024年6月总结及随笔之打卡网红点
1. 回头看 日更坚持了547天。 读《人工智能时代与人类未来》更新完成读《AI未来进行式》开更并更新完成读《AI新生:破解人机共存密码》开更并持续更新 2023年至2024年6月底累计码字1267912字,累计日均码字2317字。 2024年6月码字90659字,…...

《Windows API每日一练》7.4 状态报告上使用计时器
这一节我们使用计时器,每隔一秒获取当前鼠标坐标位置的像素值,并显示在窗口,这就相当于是一个简单的取色器了。 本节必须掌握的知识点: 第47练:取色器 7.4.1 第47练:取色器 /*----------------------------…...

python实现API调用缓存
python实现API调用缓存 1.代码2.输出3.保存的json数据 想把python某些函数的参数及返回值记录下来,如果之前已计算过,则直接返回缓存中的数据 1.代码 import jsondef get_variable_name(var):变量转变量名local_varsglobals()return [name for name, value in local_vars.ite…...
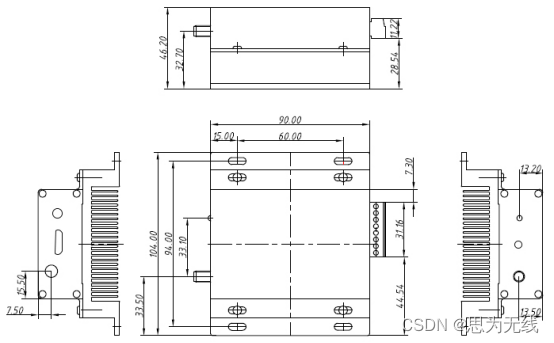
传输距离3000M|低延迟|48K采样音频传输模块-SA356大功率发射模块
无线音频应用中,远距离音频传输在许多领域具有广泛的应用需求,例如大型会议系统、公共广播、户外活动和音乐演出等。为了满足这些需求,音频传输模块需要具备一些关键特性,包括长距离传输能力、高音质、低延迟、稳定性以及抗干扰能…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
