深入理解策略梯度算法
策略梯度(Policy Gradient)算法是强化学习中的一种重要方法,通过优化策略以获得最大回报。本文将详细介绍策略梯度算法的基本原理,推导其数学公式,并提供具体的例子来指导其实现。
策略梯度算法的基本概念
在强化学习中,智能体通过与环境交互来学习一种策略(policy),该策略定义了在每个状态下采取哪种行动的概率分布。策略可以是确定性的或随机的。在策略梯度方法中,策略通常表示为参数化的概率分布,即 ,其中
是策略的参数,
是状态,
是行动。
目标是找到最佳的策略参数 $\theta$ 使得智能体在环境中获得的期望回报最大。为此,我们需要定义一个目标函数,表示期望回报。然后,通过梯度上升法(或下降法)来优化该目标函数。
策略梯度的数学推导
假设我们的目标函数 $J(\theta)$ 定义为:
其中 表示一个完整的轨迹(从初始状态到终止状态的状态-动作序列),
是该轨迹的总回报。根据策略的定义,我们有:
因此,目标函数可以重写为:
为了最大化,我们需要计算其梯度
:
使用概率分布的梯度性质,我们有:
因此,梯度可以表示为:
这个公式被称为策略梯度定理。为了估计这个期望值,我们通常使用蒙特卡洛方法,从策略 中采样多个轨迹
,然后计算平均值。
策略梯度算法的实现
我们以一个简单的环境为例,展示如何实现策略梯度算法。假设我们有一个离散动作空间的环境,我们使用一个神经网络来参数化策略。
步骤 1:环境设置
首先,设置环境和参数:
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optimenv = gym.make('CartPole-v1')
n_actions = env.action_space.n
state_dim = env.observation_space.shape[0]
步骤 2:策略网络定义
定义一个简单的策略网络:
class PolicyNetwork(nn.Module):def __init__(self, state_dim, n_actions):super(PolicyNetwork, self).__init__()self.fc1 = nn.Linear(state_dim, 128)self.fc2 = nn.Linear(128, n_actions)def forward(self, x):x = torch.relu(self.fc1(x))x = self.fc2(x)return torch.softmax(x, dim=-1)policy = PolicyNetwork(state_dim, n_actions)
optimizer = optim.Adam(policy.parameters(), lr=0.01)
步骤 3:采样轨迹
编写函数来从策略中采样轨迹:
def sample_trajectory(env, policy, max_steps=1000):state = env.reset()states, actions, rewards = [], [], []for _ in range(max_steps):state = torch.FloatTensor(state).unsqueeze(0)probs = policy(state)action = np.random.choice(n_actions, p=probs.detach().numpy()[0])next_state, reward, done, _ = env.step(action)states.append(state)actions.append(action)rewards.append(reward)if done:breakstate = next_statereturn states, actions, rewards
步骤 4:计算回报和梯度
计算每个状态的回报,并使用策略梯度定理更新策略:
def compute_returns(rewards, gamma=0.99):returns = []G = 0for r in reversed(rewards):G = r + gamma * Greturns.insert(0, G)return returnsdef update_policy(policy, optimizer, states, actions, returns):returns = torch.FloatTensor(returns)loss = 0for state, action, G in zip(states, actions, returns):state = state.squeeze(0)probs = policy(state)log_prob = torch.log(probs[action])loss += -log_prob * Goptimizer.zero_grad()loss.backward()optimizer.step()
步骤 5:训练策略
将上述步骤组合在一起,训练策略网络:
num_episodes = 1000
for episode in range(num_episodes):states, actions, rewards = sample_trajectory(env, policy)returns = compute_returns(rewards)update_policy(policy, optimizer, states, actions, returns)if episode % 100 == 0:print(f"Episode {episode}, total reward: {sum(rewards)}")
总结
通过以上步骤,我们实现了一个基本的策略梯度算法。策略梯度方法通过直接优化策略来最大化智能体的期望回报,具有理论上的简洁性和实用性。本文详细推导了策略梯度的数学公式,并提供了具体的实现步骤,希望能够帮助读者更好地理解和应用这一重要的强化学习算法。
相关文章:
深入理解策略梯度算法
策略梯度(Policy Gradient)算法是强化学习中的一种重要方法,通过优化策略以获得最大回报。本文将详细介绍策略梯度算法的基本原理,推导其数学公式,并提供具体的例子来指导其实现。 策略梯度算法的基本概念 在强化学习…...

Unicode 和 UTF-8 以及它们之间的关系
通俗易懂的 Unicode 和 UTF-8 解释 Unicode 是什么? 想象一下,我们有一个巨大的图书馆,这个图书馆里有各种各样的书,每本书都有一个唯一的编号。Unicode 就像是这个图书馆的目录系统,它给世界上所有的字符࿰…...

【C++】多态详解
💗个人主页💗 ⭐个人专栏——C学习⭐ 💫点击关注🤩一起学习C语言💯💫 目录 一、多态概念 二、多态的定义及实现 1. 多态的构成条件 2. 虚函数 2.1 什么是虚函数 2.2 虚函数的重写 2.3 虚函数重写的两个…...

C#异常捕获
前言 在C#中,我们无法保证我们编写的程序没有一点bug,如果我们对于这些抛出异常的bug不进行任何的处理的话,那么我们的软件在抛出这些异常的时候就会崩溃,也就是软件闪退,并且这种闪退由于我们没有进行处理࿰…...

工业一体机根据软件应用需求灵活选配
在当今工业领域,数字化、智能化的发展趋势愈发明显,工业一体机作为关键的设备,其重要性日益凸显。而能够根据软件应用需求进行灵活选配的工业一体机,更是为企业提供了高效、定制化的解决方案。 一、工业一体机的全封闭无风扇散热功…...
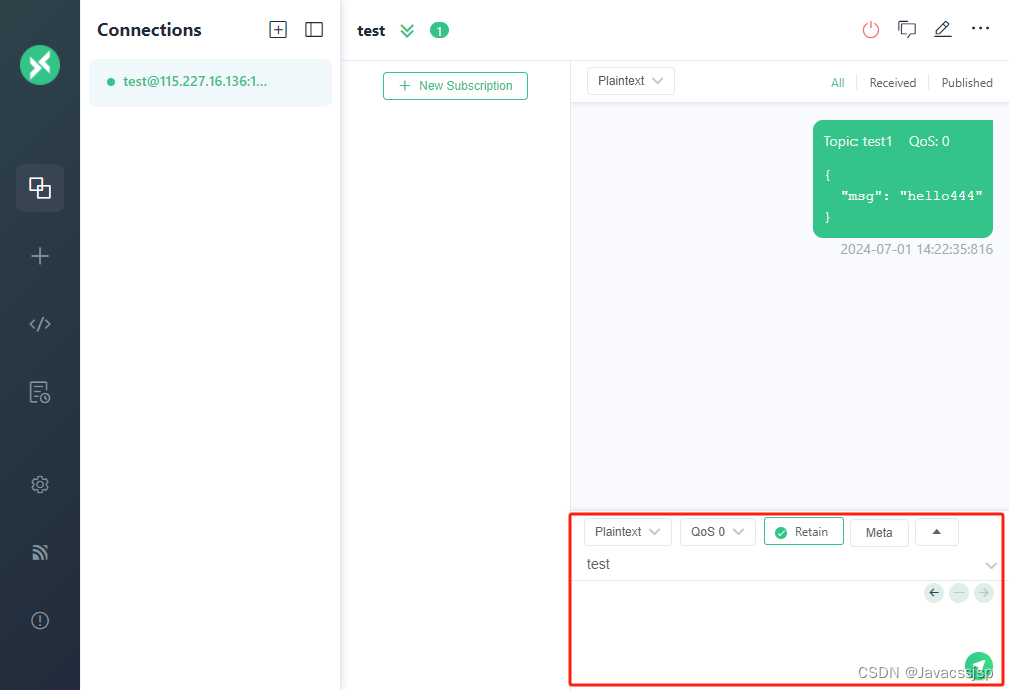
centos7 mqtt服务mosquitto搭建记录
1、系统centos7.6,安装默认版本 yum install mosquitto 2、启动运行 systemctl start mosquitto 3、设置自启动 systemctl enable mosquitto 4、修改配置文件 vim /etc/mosquitto/mosquitto.conf 监听端口,默认为1883,需要修改删除前面…...

双阶段目标检测算法:精确与效率的博弈
双阶段目标检测算法:精确与效率的博弈 目标检测是计算机视觉领域的一个核心任务,它涉及在图像或视频中识别和定位多个对象。双阶段目标检测算法是一种特殊的目标检测方法,它通过两个阶段来提高检测的准确性。本文将详细介绍双阶段目标检测算…...

Python量化交易策略
策略详情 按照1分k线图;跳过9:30点1分k线图不计算 买入;监控市面的可转债;当某1分涨幅大于x涨幅,一直重复x次,选择买入,符合x设置的条件只选择成交额最大的可转债买入(x要自定义&…...
为什么我感觉 C 语言在 Linux 下执行效率比 Windows 快得多?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「Linux的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!!Windows的终端或者叫控制台…...

算法导论 总结索引 | 第四部分 第十六章:贪心算法
1、求解最优化问题的算法 通常需要经过一系列的步骤,在每个步骤都面临多种选择。对于许多最优化问题,使用动态规划算法求最优解有些杀鸡用牛刀了,可以使用更简单、更高效的算法 贪心算法(greedy algorithm)就是这样的算…...

用“文心一言”写的文章,看看AI写得怎么样?
零售连锁店的“支付结算”业务设计 在数字化浪潮的推动下,连锁店零售支付结算的设计愈发重要。一个优秀的支付结算设计不仅能够提升用户体验,还能增强品牌竞争力,进而促进销售增长。 本文将围绕一个具体的连锁店零售支付结算案例…...

企业消费采购成本和员工体验如何实现“鱼和熊掌“的兼得?
有企业说企业消费采购成本和员工体验的关系好比是“鱼和熊掌”,无法兼得? 要想控制好成本就一定要加强管控,但是加强管控以后,就会很难让员工获得满意的体验度。如果不加以管控,员工自由度增加了,往往就很难…...

发表EI论文相当于SCI几区?
EI(工程索引)本身并不进行分区,它是一个收录工程领域高质量文献的数据库,与SCI(科学引文索引)的分区制度不同。然而,在非正式的学术评价中,有时人们会将EI与SCI的分区进行比较。 虽…...

STFT短时傅里叶变换MTLAB简析
代码: 解释: 如果信号x有Nx个时间样本,短时傅里叶变换的结果矩阵s有k列; k的计算方式如图所示,M是窗函数的长度,L是重叠长度。 此符号是向下取整符号。 短时傅里叶变换的结果矩阵s的行数与参数‘FFTLength’…...

海致科技实施实习生面试
一、面试内容 注:此次是电话面试 1.是XX先生吗 2.你是有考虑转实施的吗? 3.请讲一下你对项目部署实施的理解和掌握 4.用过数据库,会编写SQL语句吗? 5.讲一下SQL的常用关键字 6.了解SQL中的函数吗?谈谈函数 7.多…...

论文阅读之旋转目标检测ARC:《Adaptive Rotated Convolution for Rotated Object Detection》
论文link:link code:code ARC是一个改进的backbone,相比于ResNet,最后的几层有一些改变。 Introduction ARC自适应地旋转以调整每个输入的条件参数,其中旋转角度由路由函数以数据相关的方式预测。此外,还采…...
)
面向对象(Java)
构造方法只能在对象实例化的时候调用 this可以作为方法参数,表示调用方法的当前对象 this可以作为方法返回值,表示返回当前对象 封装 通过方法访问数据,隐藏类的实现细节 static:类对象共享,类加载时产生,…...

I/O多路复用
参考面试官:简单说一下阻塞IO、非阻塞IO、IO复用的区别 ?_unix环境编程 阻塞io和非阻塞io-CSDN博客 同步阻塞(BIO) BIO 以流的方式处理数据 应用程序发起一个系统调用(recvform),这个时候应用程序会一直阻塞下去&am…...

线性代数基础概念:向量空间
目录 线性代数基础概念:向量空间 1. 向量空间的定义 2. 向量空间的性质 3. 基底和维数 4. 子空间 5. 向量空间的例子 总结 线性代数基础概念:向量空间 向量空间是线性代数中最基本的概念之一,它为我们提供了一个抽象的框架,…...

php 抓取淘宝商品评论数据 json
要抓取淘宝商品评论数据,你可以使用PHP的cURL库来发送HTTP请求并获取JSON格式的数据。 API接入流程:需要开放平台或者是封装接口注册账号,并申请相应的API使用权限,以获取必要的密钥和接口文档。获取接口使用权限:接入…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
