7 动态规划
下面的例子不错: 对于动态规划,能学到不少东西;
你要清楚每一步都在做什么,划分细致就能够拆解清楚!
xk. - 力扣(LeetCode)
labuladong的算法笔记-动态规划-CSDN博客
动态规划是一种强大的算法设计策略,用于解决具有重叠子问题和最优子结构特点的问题。在面对动态规划类题目时,遵循以下步骤可以帮助你系统地解决问题:
1. 定义状态
- 确定变量:识别哪些变量会影响问题的解。例如,在背包问题中,关键变量可能是物品的重量和价值,以及剩余的背包容量。
- 状态表示:用这些变量定义状态。例如,
dp[i][w]可能表示前i个物品放入容量为w的背包所能获得的最大价值。2. 状态转移方程
- 建立关系:找到状态之间的关系,即如何从一个状态转移到另一个状态。这通常涉及到一个递推公式。例如,在斐波那契数列中,
F(n) = F(n-1) + F(n-2)。- 边界条件:确定递推公式的起始状态,通常是最简单的情况,例如
dp[0][w] = 0(背包问题中没有物品时的价值)。3. 选择方向
- 自底向上:从最简单的状态开始,逐步构建更复杂的状态。这种方法通常使用循环实现,避免了重复计算。
- 自顶向下:从复杂的状态开始,递归地解决子问题。这种方法通常使用递归和记忆化(memoization)来避免重复计算。
4. 初始化
- 初始状态:根据问题的性质初始化DP数组。例如,所有状态初始化为0或无穷大。
5. 计算
- 填充DP表:根据状态转移方程填充DP表或数组。确保按正确的顺序填充,以便在计算每个状态时,所需的前驱状态已经被计算。
6. 返回结果
- 解析答案:DP过程完成后,根据问题要求解析出最终答案。这可能是DP表中的某个特定值,也可能是回溯整个DP过程找到最优解的具体方案。
7. 复杂度分析
- 时间复杂度:通常由状态的数量和状态转移的复杂度决定。
- 空间复杂度:由存储状态所需的空间决定,可以通过滚动数组等方式优化空间复杂度。
1 70. 爬楼梯
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶这是一个简单的动态规划的问题:
分解问题:不积硅步无以至千里!
假设:当前到了第x层,并且小于x层的走法f(x)我们都知道。
那么后面如何求呢?
- 第一个阶梯、第二个阶梯都是1下就能走到!
- y = x+1,那么 f(y) = f(y-1) + f(y-2), 想要上到第y步, 一定是从前面阶梯走过来的。
class Solution:def climbStairs(self, n: int) -> int:dp = [1] * (n+1)for i in range(2,n+1):dp[i] = dp[i-1] + dp[i-2]#print(dp)return dp[n]
2 198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
相邻不能同时偷!
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。在做这一个题目的时候:
f(x): 到第x个房间能得到的最大收益;
我也是设定:加入到了第X个房间,那么之前的状态(到房间能得到的最大收益)我都是知道的。所以,f(X+1) 怎么做才能最大呢?
怎么能偷到x+1个房子,由x-1过来的,x-2过来的(开始我没考虑到这点)。
class Solution:def rob(self, nums: List[int]) -> int:dp = nums[::]for i in range(2,len(nums)):temp = dp[i-2]if i-3>=0:temp = max(temp,dp[i-3])dp[i] = temp + nums[i]return max(dp)
3 322. 零钱兑换
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回
-1。你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins =[1, 2, 5], amount =11输出:3解释:11 = 5 + 5 + 1
- 递归;
- 动态规划;
有硬币:【q,w,e】
思想:
比如7个硬币怎么使用最少的硬币进行组合呢?
f(7) = min(f(7-q),f(7-w),f(7-e)) + 1
还有个特殊条件: f(7-q),f(7-w),f(7-e) 存在组合(基石,不然无法站住脚);
我这个思路不是特征的好。
class Solution:def coinChange(self, coins: List[int], amount: int) -> int:if amount==0:return 0 coins = sorted(coins)dp = [0] * (amount+1)for i in range(amount+1):for coin in coins:if i-coin==0:dp[i] = 1elif i-coin>0:if dp[i]==0:# if dp[i-coin]==0:dp[i]==0else:dp[i] = dp[i-coin] + 1 #min(, dp[i])else:if dp[i-coin]==0:dp[i]==0else:dp[i] = min(dp[i-coin] + 1, dp[i])else:breakprint(dp)return -1 if dp[amount]==0 else dp[amount]# def sub_x(amount):# if amount==0:# return 0# if amount < 0 or amount<coins[0]:# return -1# temp = -1# for coin in coins:# x = sub_x(amount - coin) # -1, >=0# if x == -1:# continue# if temp==-1:# temp = x+1# else:# temp = min(x+1, temp)# return tempreturn sub_x(amount)
思路二 :陈奕迅的背包

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:n = len(coins)dp = [[amount+1] * (amount+1) for _ in range(n+1)] # 初始化为一个较大的值,如 +inf 或 amount+1# 合法的初始化dp[0][0] = 0 # 其他 dp[0][j]均不合法# 完全背包:套用0-1背包【遍历硬币数目k】for i in range(1, n+1): # 第一层循环:遍历硬币for j in range(amount+1): # 第二层循环:遍历背包for k in range(j//coins[i-1]+1): # 第三层循环:当前硬币coin取k个 (k*coin<=amount)dp[i][j] = min( dp[i][j], dp[i-1][j-k*coins[i-1]] + k )ans = dp[n][amount] return ans if ans != amount+1 else -1相关文章:

7 动态规划
下面的例子不错: 对于动态规划,能学到不少东西; 你要清楚每一步都在做什么,划分细致就能够拆解清楚! xk. - 力扣(LeetCode) labuladong的算法笔记-动态规划-CSDN博客 动态规划是…...

.net 快速开发框架开源
DF.OpenAPI开源系统 前后端分离,开箱即用,java经典功能.net也具备 系统介绍 DF.OpenAPI是基于Admin.NET二开的,是一个开源的多租户后台管理系统。采用前后端分离技术(前端使用vue.js,后端使用.net 3~.net6ÿ…...

《昇思25天学习打卡营第06天|网络构建》
网络构建 神经网络模型由神经网络层和Tensor操作构成 #实验环境已经预装了mindspore2.2.14,如需更换mindspore版本,可更改下面mindspore的版本号 !pip uninstall mindspore -y !pip install -i https://pypi.mirrors.ustc.edu.cn/simple mindspore2.2.…...

【链表】- 两两交换链表中的节点
1. 对应力扣题目连接 两两交换链表中的节点 2. 实现案例代码 public class ExchangeLinkedListsPairwise {public static void main(String[] args) {// 示例链表:[1, 2, 3, 4]ListNode head new ListNode(1);head.next new ListNode(2);head.next.next new L…...
——抽象工厂模式)
java设计模式(四)——抽象工厂模式
一、模式介绍 改善在工厂方法模式中,扩展时新增产品类、工厂类,导致项目中类巨多的场面,减少系统的维护成本,且一个工厂可以生成多种产品,而不是同一种的产品,比如一个工厂既可以生产鞋子又可以衣服,而不是只能生产鞋子。 二、工厂方法模式 1、实现步骤 第一步: 定义…...

动物检测yolo格式数据集(水牛 、大象 、犀牛 、斑马四类)
动物检测数据集 1、下载地址: https://download.csdn.net/download/qq_15060477/89512588?spm1001.2101.3001.9500 2、数据集介绍 本数据集含有四种动物可以检测,分别是水牛 、大象 、犀牛 、斑马四类,数据集格式为yolo格式,…...

昇思25天学习打卡营第05天 | 数据变换 Transforms
昇思25天学习打卡营第05天 | 数据变换 Transforms 文章目录 昇思25天学习打卡营第05天 | 数据变换 TransformsCommon TransformsCompose Vision TransformsText TransformPythonTokenizerLookup Lambda Transforms数据处理模式Pipeline模式Eager模式 总结打卡 通常情况下的原始…...
Springboot+MySQL 公寓报修管理系统源码
功能结构图 效果图:...

jenkins 发布服务到linux服务器
1.环境准备 1.1 需要一台已经部署了jenkins的服务器,上面已经集成好了,jdk、maven、nodejs、git等基础的服务。 1.2 需要安装插件 pusblish over ssh 1.3 准备一台额外的linux服务器,安装好jdk 2.流程描述 2.1 配置jenkins,包括p…...
Appium+python自动化(三十九)-Appium自动化测试框架综合实践 - 代码实现(超详解)
1.简介 今天我们紧接着上一篇继续分享Appium自动化测试框架综合实践 - 代码实现。由于时间的关系,宏哥这里用代码给小伙伴演示两个模块:注册和登录。 2.业务模块封装 因为现在各种APP的层出不群,各式各样的。但是其大多数都有注册、登录。为…...

防止跨站脚本攻击XSS之Antisamy
目录 一、什么是跨站脚本攻击(XSS) 二、通常有哪些解决方案 三、常见的XSS攻击例子有哪些 3.1 存储型XSS攻击(黑产恶意截流,跳转不法网站) 3.2反射型XSS攻击: 四、什么是跨站请求伪造? 五…...

Python爬虫实战案例——王者荣耀皮肤抓取
大家好,我是你们的老朋友——南枫,今天我们一起来学习一下该如何抓取大家经常玩的游戏——王者荣耀里面的所有英雄的皮肤。 老规矩,直接上代码: 导入我们需要使用到的,也是唯一用到的库: 我们要抓取皮肤其…...

PyTorch计算机视觉实战:目标检测、图像处理与深度学习
本书基于真实数据集,全面系统地阐述现代计算机视觉实用技术、方法和实践,涵盖50多个计算机视觉问题。全书分为四部分:一部分介绍神经网络和PyTorch的基础知识,以及如何使用PyTorch构建并训练神经网络,包括输入数据缩放…...
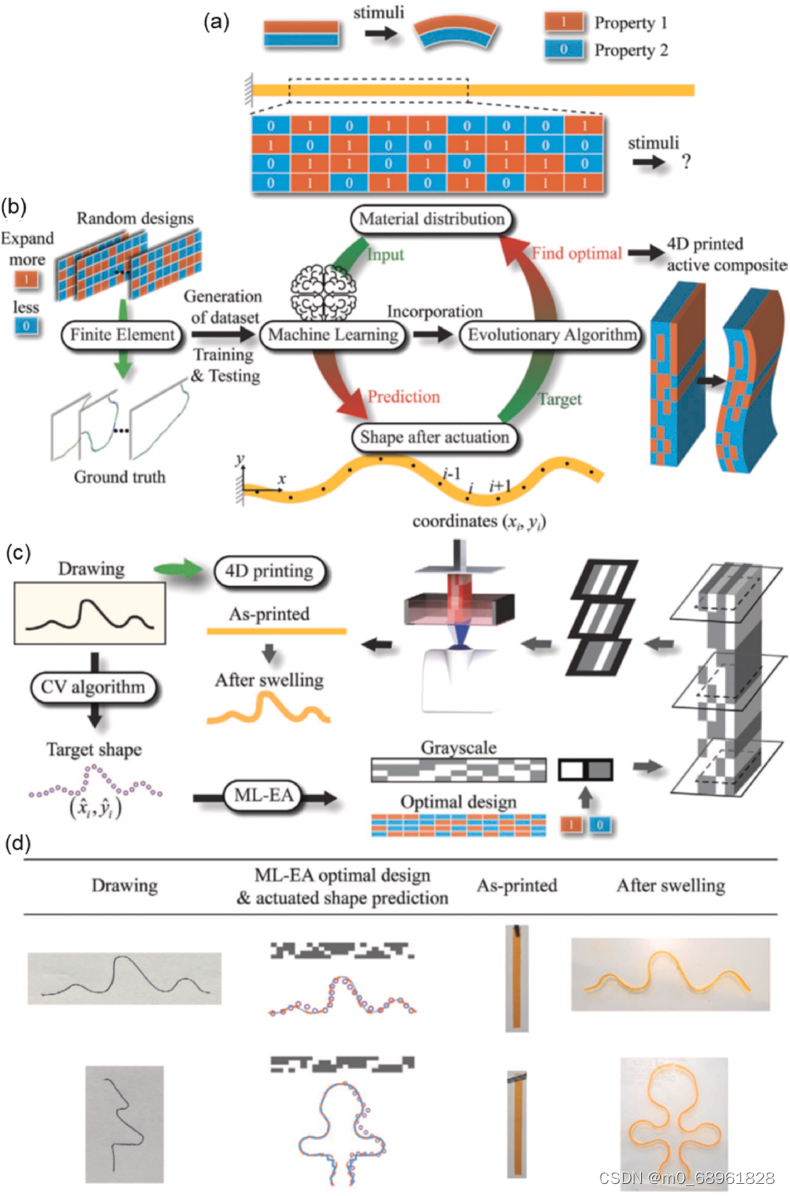
4D 生物打印:将时间维度融入,打造个性化动态组织
4D 生物打印技术将时间维度融入 3D 生物打印,赋予打印出的结构动态变化的能力,使其更接近于真实组织和器官的特性。要实现这一目标,需要使用智能生物材料和智能设计策略。 智能生物材料 目前用于 4D 生物打印的智能生物材料主要包括形状记忆…...

银行清算业务功能测试解析
银行清算业务是指银行间通过账户或有关货币当地清算系统,在办理结算和支付中用以清讫双边或多边债权债务的过程和方法。按地域划分,清算业务可分为国内联行清算和国际清算。常见的清算模式包括实时全额清算、净额批量清算、大额资金转账系统及小额定时清…...

CVE-2024-6387漏洞预警:尽快升级OpenSSH
OpenSSH维护者发布了安全更新,其中包含一个严重的安全漏洞,该漏洞可能导致在基于glibc的Linux系统中使用root权限执行未经身份验证的远程代码。该漏洞的代号为regreSSHion,CVE标识符为CVE-2024-6387。它驻留在OpenSSH服务器组件(也…...

学习整理在php中使用PHPExcel读取excel表列数大于Z时读取不到的解决方案
php读取excel列数大于Z时读取不到 背景解决方案关键代码 背景 表格数据超过26列, 也就是在Z列之前没有AA列及以后的情况, 测试一直都没有问题,超过,就会获取不到数据了 解决方案 private function getExcelData(){//获取excel文…...

python sklearn机械学习-数据预处理
🌈所属专栏:【机械学习】✨作者主页: Mr.Zwq✔️个人简介:一个正在努力学技术的Python领域创作者,擅长爬虫,逆向,全栈方向,专注基础和实战分享,欢迎咨询! 您…...

搜索引擎常用语法
引号 (" "): 用双引号将词组括起来,搜索引擎将返回包含完全相同短语的结果。 示例:"人工智能发展趋势" 减号 (-): 在关键词前加上减号可以排除包含特定词语的结果。 示例:人工智能 -机器学习(排除包含 “机器…...

华为智能驾驶方案剖析
华为ADS智驾方案始终坚持激光雷达毫米波雷达摄像头的多传感器融合路线,行业降本压力下硬件配置从超配逐步转向贴合实际需求,带动整体硬件成本下降。 1)单车传感器数量呈现下降趋势,包括激光雷达从3个减配至1个、毫米波雷达从6R减配至3R、摄像…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

