算法第十七期——状态规划(DP)之动态压缩
一、总述
状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式。
- 应用背景:以集合为状态,且集合可以用二进制来表示,用二进制的位运算来处理。
- 集合问题一般是指数复杂度的,例如:(1)子集问题,设元素无先后关系,那么共有
个子集;(2)排列问题,对所有元素进行全排列,共有n!个全排列。
- 状态压缩DP:集合的状态(子集或排列),如果用二进制表示状态,并用二进制的位运算来遍历和操作,又简单又快。
- 题目的数据范围不超过100
很多棋盘问题都运用到了状压,同时,状压也很经常和BFS及DP连用。
状压dp其实就是将状态压缩成2进制来保存,其特征就是看起来有点像搜索,每个格子的状态只有1或0 ,是另一类非常典型的动态规划
举个例子:有一个大小为n*n的农田,我们可以在任意处种田,现在来描述一下某一行的某种状态:
设n = 9;有二进制数 100011011(九位),每一位表示该农田是否被占用,1表示用了,0表示没用,这样一种状态就被我们表示出来了:见下表
2、位运算
用位运算做集合操作
判断a的第i位(从最低位开始数)是否等于1: 1<<( i -1 ) ) & a
把a的第i位改成1: a | ( 1<<(i-1) )
把a的第i位改成0: a &(~(1<<i) )
把a的最后一个1去掉: a& (a-1)
a = 213;b = 45 # a = 1101 0101,b = 0010 1101
print("a & b =", a & b) # AND = 5,二进制0001 0101
print("a | b =",a | b) # OR= 253,二进制1111 1101
print("a^ b =",a^ b) # XOR= 248,二进制1100 1100
print("a << 2 =", a<< 2) # a*4= 852,二进制0011 0101 0100
print("a >> 2=", a >> 2) # a/4 = 53,二进制0011 0101i = 5 # a的第i位是否为1
if((1 << (i-1)) & a): print("a[%d]=%d"%(i,1));#a的第i位是1
else: print("a[%d]=%d"%(i,O));#a的第i位是0a = 43;i = 5 #a = 0010 1011
print("a=", a |(1<<(i-1))) # 把a的第i位改成1。a=59,二进制0011 1011
print("a=", a &(~(1<<(i-1)))) # 把a的第i位改成0a = 242 # 把a最后的1去掉。 a =1111 0010
print("a=", a & (a-1)) # 去掉最后的1。=240,二进制1111 0000
3、引导题:糖果
2019年省赛
题目描述
糖果店的老板一共有 M 种口味的糖果出售。为了方便描述,我们将 M 种口味编号 1∼ M。
小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果,而是 K 颗一包整包出售。幸好糖果包装上注明了其中 K 颗糖果的口味,所以小明可以在买之前就知道每包内的糖果口味。给定 N 包糖果,请你计算小明最少买几包,就可以品尝到所有口味的糖果。
输入描述
第一行包含三个整数 N,M,K。
接下来 N 行每行 K 个整数 T1,T2,⋅⋅⋅,TK,代表一包糖果的口味。
其中,对于30%的评测用例,1<N<20。对于所有评测样例,1<N<100,1≤M<20,1K <20,1≤Ti≤M。)
输出描述
输出一个整数表示答案。如果小明无法品尝所有口味,输出 −1。
输入输出样例
输入
6 5 3 1 1 2 1 2 3 1 1 3 2 3 5 5 4 2 5 1 2输出
2
暴力法
- 对n包糖果做任意组合,找到其中一种组合,能覆盖所有口味,并且需要的糖果包数量最少。
- n包糖果的组合共有
种,暴力法只能通过30%的测试。
- 再用set()对每一种组合进行去重,看看那种组合能否覆盖所有口味。
DP
(1)定义状态dp[i]:表示得到口味组合 i(有i种口味) 所需要的最少糖果包数量。(当i=M就是答案)
(2)状态转移。往口味组合i中加入一包糖果,得到新的口味组合j,说明从i到j需要糖果包数量dp[i]+1。若原来的dp[j]大于dp[i]+1,说明原来得到j的方法不如现在的方法,更新dp[j] = dp[i]+1。
关键问题:如何表示口味组合。
1、普通方法:为每一包糖果定义一个大小为m的数组(以表示m种口味),记录它的口味。n包糖果的口味是一个n*m的二维数组,定义为kw[n][m]。
- 例:设共有m=10种口味,kw[1][ ] ={0,0,0,0,0,1,0,1,1,0},表示第一包糖果的口味有三种。
2、状态压缩:记录一包糖果的口味,用二进制数表示。
- 例:一包里面有3颗糖果,分别是“2,3,5”三种口味,用一个二进制数“10110”表示,这个二进制数的每一位表示一种口味。
- 使用状态压缩之后,原来需要用二维数组kw[n][m]才能表示n包糖果的口味,现在只需要一个一维数组kw[n] 。
- 例如kw[1] = 10110,表示第一包的口味是“2,3,5”三种。
- 状态压缩DP的代码写起来很简洁,因为可以用位运算来简化代码。
1、用状态压缩表示糖果口味
例:输入一包糖果的“2,3,5”三种口味。
把这3个口味压缩成二进制数10110,做“移位 << ”和“或 | ”操作。
- (1)定义初始值tmp = 0。(初始口味为0)
- (2)输入口味“2”。
先移位1<<(2-1),得二进制数10;然后再与tmp或,得tmp = tmp | 10 = 10。
- (3)输入口味“3”。
先移位1<<(3-1),得二进制数100;然后再与tmp或,得tmp = tmp | 100 = 110。
- (4)输入口味“5”。
先移位1<<(5-1),得二进制数10000;然后再与tmp或,得tmp = tmp | 10000 = 10110。
代码:tmp |= (1<<x-1)
2、dp[ ]中状态压缩的处理
dp[i]:i 表示口味,用状态压缩表示; dp[i]表示得到口味i的最少糖果包数量。
状态转移:同样用到二进制的“或”操作。例如tmp表示某一包的糖果口味,那么dp[i | tmp]就表示得到口味 i | tmp所需要的最少糖果包数量。
代码:
n, m, k = map (int,input (). split())
tot = (1 <<m)-1 # tot:二进制是m个1,表示所有m种口味
dp = [-1 for _ in range(1 << 20)] # 初始化为-1,因为无解时输出-1
dp[0] = 0 # 初始化为0,代表0包糖果有0种口味
kw = []
for _ in range (n):kw.append([int(i) for i in input ().split()]) # kw是二维矩阵
for c in kw: # 按行遍历每包糖果tmp = 0for x in c: tmp |= (1 <<(x-1)) # 遍历这包糖果的口味for i in range(tot+1): # 遍历所有组合if (dp[i] == -1): continue # 不存在得到口味i的最少糖果包数量newcase = i | tmp # 加上新的一包后的新的口味组合if (dp[newcase] == -1) or (dp[newcase] > dp[i] +1): # 新的口味之前没算过或者包数比之前多dp[newcase] = dp[i] +1
print(dp[tot]) # 得到所有口味tot的最少糖果包数量
第二行代码解释:例如m=5,(1<<m)=100000 ,那么(1<<m)-1 = 11111,表示五种口味。
复杂度:for循环,tot=2m;for循环n次,总复杂度O(n2m),本题n=100,m=20,约为一亿次。
例题:矩阵计数
题目描述
一个 N×M 的方格矩阵,每一个方格中包含一个字符 O 或者字符 X。
要求矩阵中不存在连续一行 3 个 X 或者连续一列 3 个 X。
问这样的矩阵一共有多少种?
输入描述
输入一行包含两个整数 N,M (1≤N,M≤5)。
输出描述
输出一个整数代表答案。
输入输出样例
输入
2 3输出
49
思路:
- 很直接的状态压缩DP。
- 把方格中的字符‘0’看成数字0,字符‘X’看成数字1。
- 把每一行看成一个m位的二进制数,例如一行字符“OOXOX”对应二进制数“00101”。
- 一行数字有
种情况,即范围[0,1<<m)内的数字。这些数字里面只有部分数字符合要求,把这些数存进一个数组 row[ ]。
- 要求:这个数字中没有连续的3个1。一个符合要求的数就是这一行的一个合法状态。
做法
- 定义状态dp[i][i][k]:第i行的合法状态为j,前一行的合法状态为k时,符合条件的矩阵有多少个。(处理比较连续三行的定义方法)
- 连续3行的情况:设第i行状态为j,前一行状态为k,再前面一行状态为p,那么j & k& p等于0,说明这3行没有一列上是3个1。这3行是一种合法状态。
- 状态的递推:
if j & k & p==0:
dp[i][i][k] += dp[i- 1][k][p]
代码
check (x) :
检查一行(用x表示这一行)里面有没有连续的3个1
dp[ ][ ][ ]:定义三维的dp
dp[i][][k]:第i行的合法状态为j,前一行的合法状态为k时,符合条件的矩阵有多少个
def check(x): #检查x中有没有连续3个1num = 0while x:if x & 1:num += 1 # 从第一位开始,发现一个1else:num = 0 # 没有1则重置为0if num == 3: return False # 有连续3个1x >>= 1 #右移一次return True # 没有连续三个1,满足要求
N,M = list(map(int, input ().split()))
s = 2**M
row = [] # 合法的行
for i in range(s): # i的范围:00000~11111if check(i): row.append(i) # 加入合法的行
dp = [[[0 for i in range(s)] for j in range(s)] for k in range (N)] # 初始化dp
for i in row :dp[0][i][0]= 1 # 初始化第0行的符合条件的矩阵数均为1
# 遍历第1~N-1行,统计满足要求的矩阵数量
for i in range(1, N): # 1~N-1# 对每一行遍历合法行的情况下,再检查连续3列(当前一行和前两行)是否合法for j in row: for k in row:for p in row:if j & k & p == 0: # 连续三列不是三个1dp[i][j][k] += dp[i - 1][k][p]
ans = 0
for j in row :ans += sum(dp[N - 1][j]) # 对最后一行求和,其中sum(dp[N - 1][j])是求最后一行的第j中合法状态的和
print(ans)
复杂度:4个for循环m
例题:回路计数
题目描述
蓝桥学院由 21 栋教学楼组成,教学楼编号 1 到 21。对于两栋教学楼 a 和 b,当 a 和 b 互质时,a 和 b 之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
小蓝现在在第一栋教学楼,他想要访问每栋教学楼正好一次,最终回到第一栋教学楼(即走一条哈密尔顿回路),请问他有多少种不同的访问方案?
两个访问方案不同是指存在某个i,小蓝在两个访问方法中访问完教学楼 i 后访问了不同的教学楼。
提示:建议使用计算机编程解决问题。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
Hami lton问题
- Hamilton问题是NP问题,没有多项式复杂度的解法。
- 暴力解法:枚举n个点的全排列。共n!个全排列,一个全排列就是一条路径。本题n=21,21! = 51,090,942,171,709,440,000
- 用状态压缩DP,复杂度下降为
- 参考:《算法竞赛》341页,或者csdn搜“罗勇军”找到“状态压缩DP”
状态压缩DP
- 路径起点是1,绕一圈回到1。
- 问题转化:1先到2~21中的某个点,然后再绕一圈回到1。
- 定义DP。设S是图的一个子集,用dp[S][j]表示“集合S内的Hamilton路径个数”, 即从起点1出发经过 S中所有点 ,到达 终点j 时的路径个数。
- 最后求所有的访问方案:累加所有的dp[X][2]~dp[X][21]。其中X = 1 << 22 - 2(-2是两个-1,-1是改造21个1,-1是把起点1置为0),X是除了点1以外的所有其他点。
哈密尔顿问题与DP
- 如何求dp[S][ ]? 从小问题S-j递推到大问题S。S - j 表示从集合S中去掉j,即
不包含j点的集合。
- 如何从S-j递推到S? 设k是S-j中一个点,把从1到j的路径分为两部分: ( 1→...→k)+(k→j)。以k为变量枚举S-j中所有的点
- 状态转移方程: dp[S][j]+=dp[S-j][k]
- 代码:dp[S][j] += dp[S - (1<<j)][k]

代码:
初始化:
教学楼编号1到21。教学楼a和b,当a和b互质时,a和b之间有一条走廊直接相连,两个方向皆可通行,否则没有直接连接的走廊。
from math import gcdm = 1 << 22
dp = [[0 for j in range(22)] for i in range(m)]
dist = [[False for j in range(22)] for i in range(22)] # 记录联通关系
for i in range(1, 22):for j in range(1, 22):if gcd(i, j) == 1: # 最小公因数为1,互质dist[i][j] = True
dp[2][1] = 1 # 初始化dp
for S in range(2, m - 1): # 遍历所有集合Sfor j in range(1, 22): # 从21个抽一个j出来if S >> j & 1: # 集合S中包括jfor k in range(1, 22):if S - (1 << j) >> k & 1 and dist[k][j]: # 集合S-j包括k,且k和j联通dp[S][j] += dp[S - (1 << j)][k] # 累加S-j集合
ans = 0
for i in range(2, 22): ans += dp[m - 2][i]
print(ans)
# 881012367360
复杂度:3个for循环
m=221212=924,844,032,运行时间长达5分钟,所以这是一道填空题。
相关文章:
算法第十七期——状态规划(DP)之动态压缩
一、总述 状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式。 应用背景:以集合为状态,且集合可以用二进制来表示,用二进制的位运算来处理。集合问题一般是指数复杂度的&#x…...
网络安全竞赛试题A模块第八套解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A模块第八套解析(详细)
2022年全国职业院校技能大赛(中职组) 网络安全竞赛试题 (8) (总分100分) 赛题说明 一、竞赛项目简介 “网络安全”竞赛共分A.基础设施设置与安全加固;B.网络安全事件响应、数字取证调查和应用安全;C.CTF夺旗-攻击;D.CTF夺旗-防御等四个模块。根据比赛实际情况,竞…...

【华为OD机试真题 JAVA】数组中是否存在满足规则的数字组合
标题:数组中是否存在满足规则的数字组合 | 时间限制:1秒 | 内存限制:262144K | 语言限制:不限 给定一个正整数数组,检查数组中是否存在满足规则的数字组合 * 规则: * A = B + 2C 输入描述: * 第一行输出数组的元素个数。 * 接下来一行输出所有数组元素,用空格…...

【OpenCV技能树】——OpenCV基础
前言: 😊😊😊欢迎来到本博客😊😊😊 目前正在进行 OpenCV技能树的学习,OpenCV是学习图像处理理论知识比较好的一个途径,至少比看书本来得实在。本专栏文章主要记录学习Op…...

人体姿态识别
自留记录论文阅读,希望能了解我方向的邻域前沿吧 粗读,持续更新 第一篇 ATTEND TO WHO YOU ARE: SUPERVISING SELF-ATTENTION FOR KEYPOINT DETECTION AND INSTANCE-AWARE ASSOCIATION 翻译:https://editor.csdn.net/md?not_checkout=1&spm=1001.2014.3001.5352&…...

ubuntu下调试驱动
使用 Ubuntu Linux 测试 Linux 驱动 1. 测试 Linux 驱动准备工作 对于一个 Linux 驱动程序,一开始可以在 Ubuntu Linux 上做前期开发和测试。对于访问硬件部分也可以在 Ubuntu Linux 用软件进行模拟,切记不能代替真实的环境!当基本开发完成后&#…...
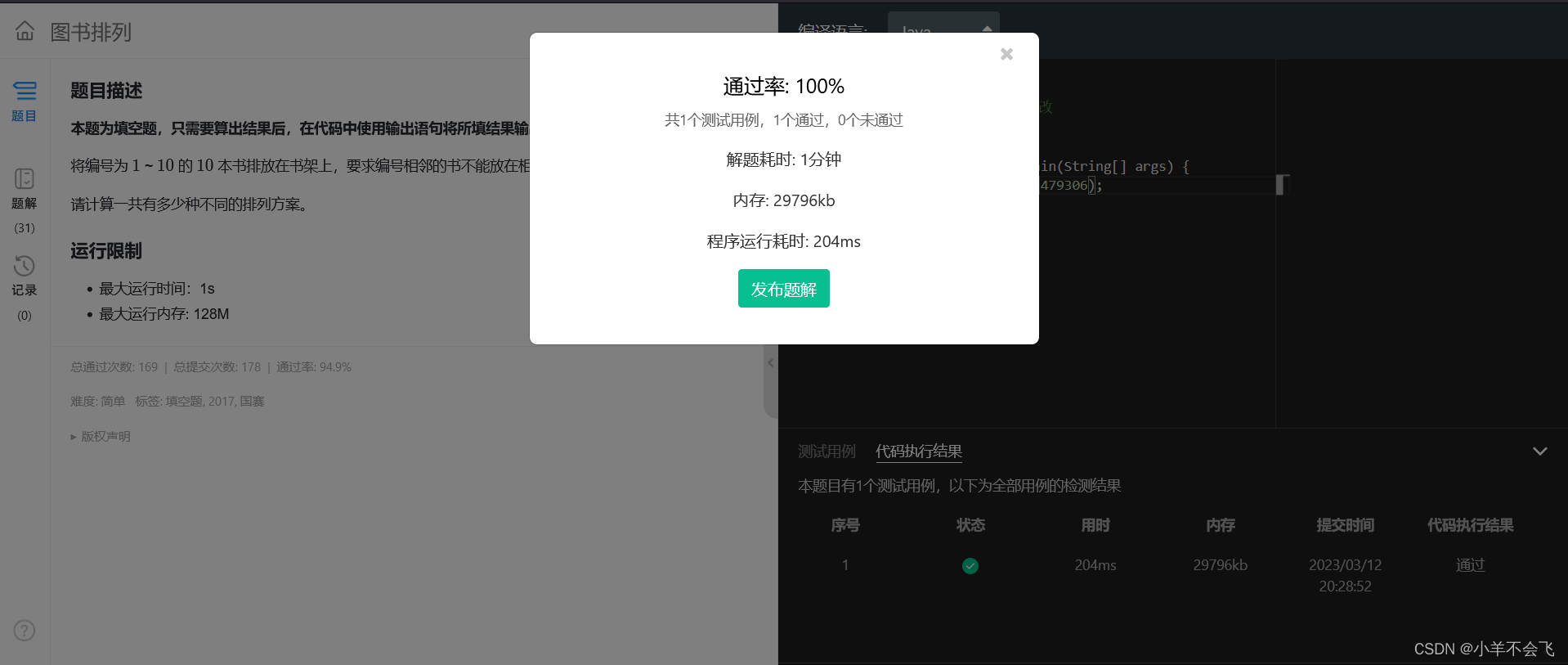
第十四届蓝桥杯三月真题刷题训练——第 9 天
第 1 题:找素数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 素数就是不能再进行等分的整数。比如:7,11。而 9 不是素数,因为它可以平分为 3 等份。一般认为最小的…...

操作系统复习
熟练掌握操作系统的定义,操作系统的特征,操作系统的功能熟练掌握多道程序设计的概念,单道程序设计和多道程序设计的区别,多道程序设计的优点熟悉操作系统接口的主要功能,系统调用的基本概念、类型、实现。操作系统接口…...
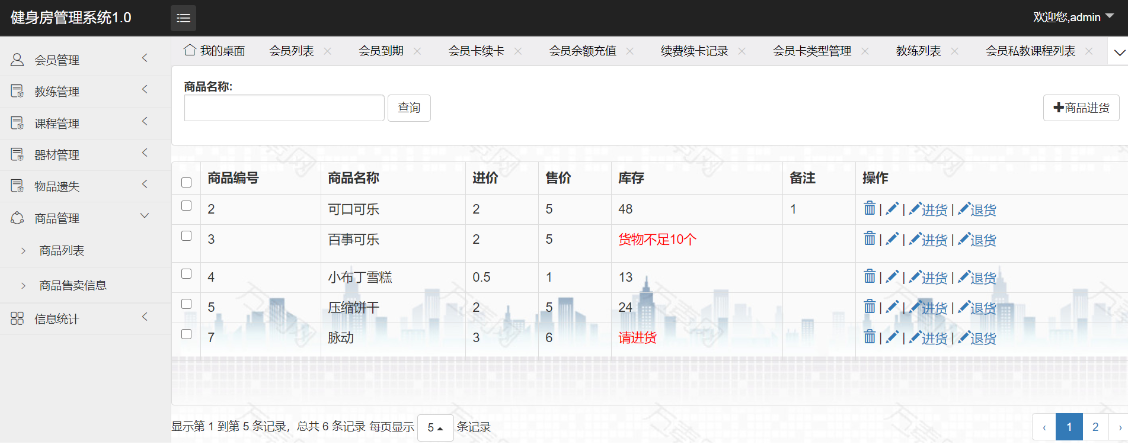
springboot健身房管理系统
springboot健身房管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍…...

C语言学习笔记——数组
前言 数组是C语言中的一种自定义数据类型,它的使用非常广泛。但是很多新手在使用数组时,经常在一些细节上出问题,导致程序崩溃或者无法编译。今天,我就来详细聊聊数组的使用和我注意到的一些细节。 一、常见的数组类型与数组的创建…...

类和对象 - 中
本文已收录至《C语言》专栏! 作者:ARMCSKGT 目录 前言 正文 构造函数 对比C和C的初始化 构造函数的使用与特性 默认构造函数 C11关于默认构造缺陷的补丁 析构函数 析构函数特性 默认析构和自定义析构 拷贝构造函数 问题聚焦 拷贝构造的定…...
Android之屏幕适配方案
在说明适配方案之前,我们需要对如下几个概念有所了解:屏幕尺寸,屏幕分辨率,屏幕像素密度。 屏幕尺寸 屏幕尺寸指屏幕的对角线的物理长度,单位是英寸,1英寸2.54厘米。 比如常见的屏幕尺寸:5.0、5…...

SpringBoot+jersey跨域文件上传
一、配置tomcat服务器 1.1、添加upload文件夹 在webapps\Root文件夹下创建用于接收上传文件的upload文件夹 1.2、修改conf\web.xml设置允许上传文件 <init-param><param-name>readonly</param-name><param-value>false</param-value></ini…...

数据结构One——绪论
本喵是FW视频封面最终版宝子,你不点个赞吗?不评个论吗?不收个藏吗? 最后的最后,关注我,关注我,关注我,你会看到更多有趣的博客哦!!! 喵喵喵&#…...
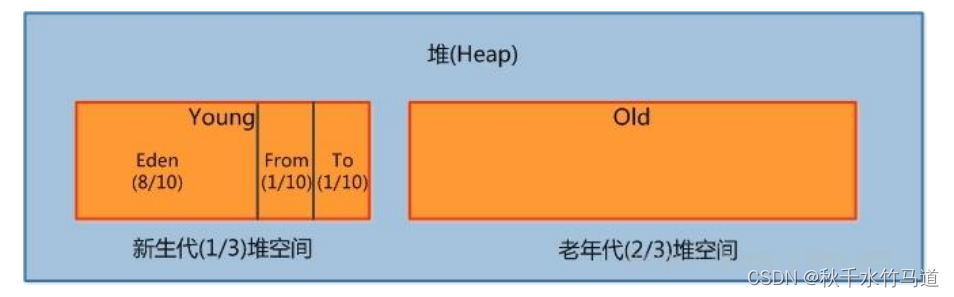
JVM篇之内存及GC
目录一、JVM内存区域1.1程序计数器1.2虚拟机栈1.3本地方法栈1.4堆1.5方法区二、JVM运行时内存2.1新生代(轻量级GC)2.2老年代(重量级GC)一、JVM内存区域 JVM 内存区域主要分为线程私有区域【程序计数器、虚拟机栈、本地方法栈】、线程共享区域【JAVA 堆、…...
的一些方式)
Linux驱动操作地址(寄存器)的一些方式
Linux驱动操作地址(寄存器)的一些方式 文章目录Linux驱动操作地址(寄存器)的一些方式1.对绝对地址赋值操作2. ioremap2.1 void __iomem *地址2.2 volatile unsigned int *地址2.3 structioremap1.对绝对地址赋值操作 对绝对地址0x100000赋值操作 *&…...

Java日志框架介绍
Log4j Apache Log4j是一个基于Java的日志记录工具。它是由Ceki Glc首创的,现在则是Apache软件基金会的一个项目。 Log4j是几种Java日志框架之一。 Log4j 2 Apache Log4j 2是apache开发的一款Log4j的升级产品。 Commons Logging Apache基金会所属的项目,是…...

编程中遇到的计算机大小端概念
概念大小端(Endian)是指在一个多字节的数据中,字节的存储顺序的规定。通俗来说,就是指数据在计算机内部存储时的顺序问题。在计算机系统中,一个数据项可能占据多个存储单元。在这种情况下,这个数据项的存储…...
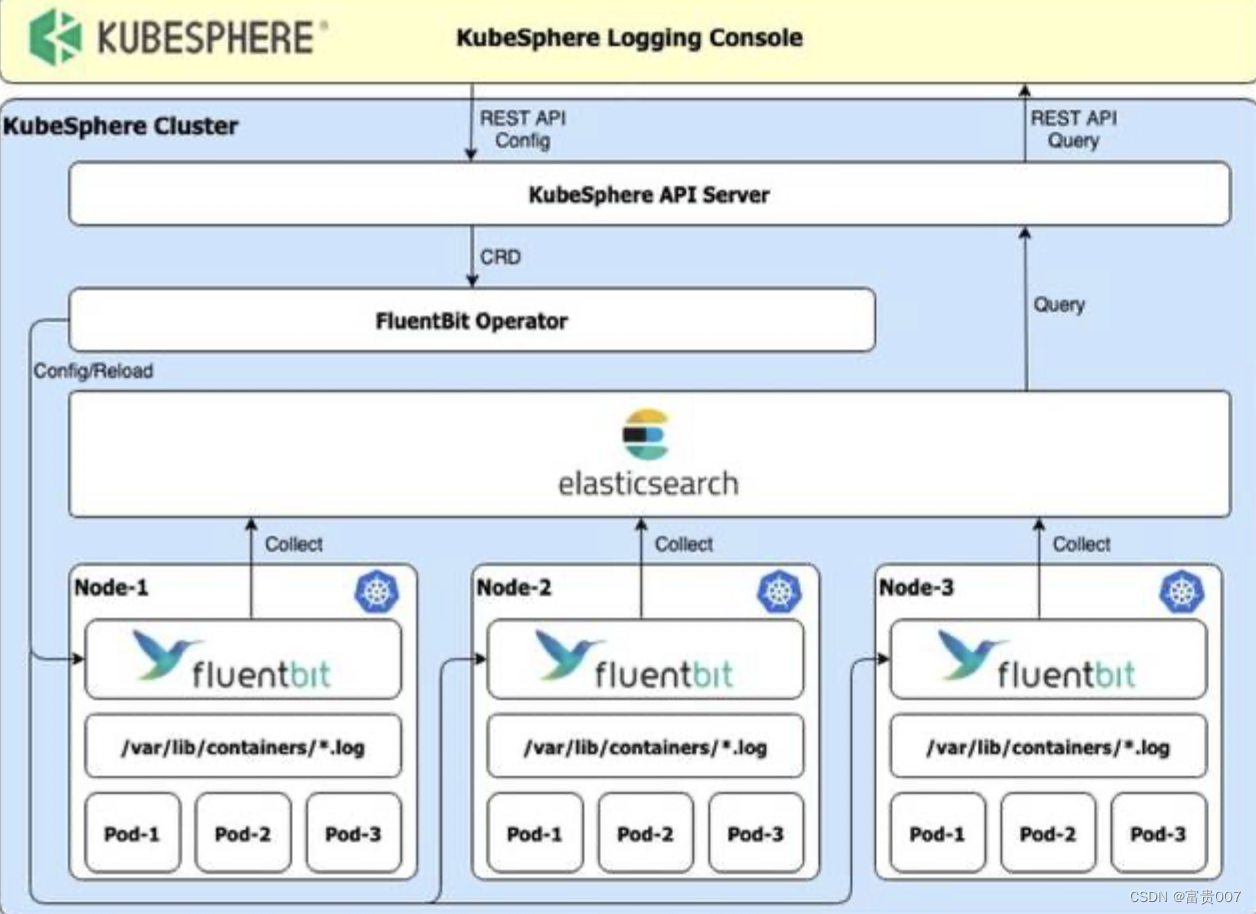
日志与可视化方案:从ELK到EFK,再到ClickHouse
EFK方案 从ELK谈起 ELK是三个开源软件的缩写,分别表示:Elasticsearch,Logstash,Kibana。新增了一个FlieBeat,它是一个轻量级的日志收集处理工具,FlieBeat占用资源少,适用于在各个服务器上搜集…...

字符函数和字符串函数(上)——“C”
各位CSDN的uu们你们好呀,今天小雅兰来给大家介绍一个全新的知识点,就是字符函数和字符串函数啦,其实其中有些函数我之前已经学习过了,比如strlen、strcpy;也有一些之前不是很熟悉的函数,比如strstr、strtok…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
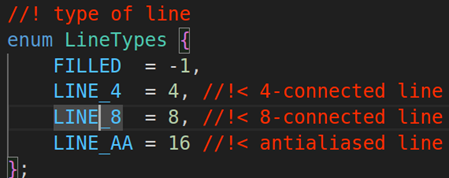
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...
