数据结构——树的基础概念
目录
1.树的概念
2.树的相关概念
3.树的表示
(1)直接表示法
(2)双亲表示法
(3)左孩子右兄弟表示法
4.树在实际中的运用(表示文件系统的目录树结构)
1.树的概念
树是一种非线性的数据结构,它是由n(n>=0个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。我们现实中的树是这样的:

而我们数据结构中的树是这样的:
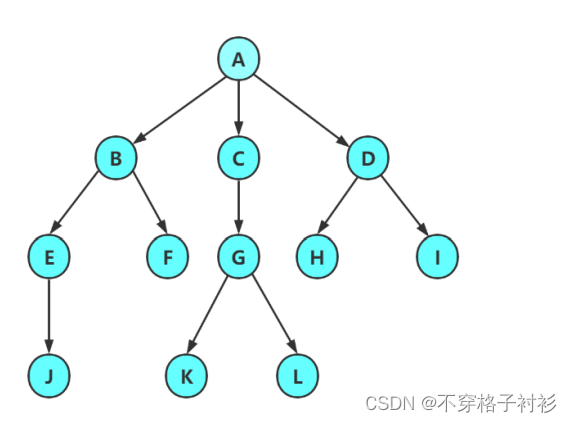
有一个特殊的结点,称为根结点,根结点没有前驱结点除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1又是一棵结构与树类似的子树。
每棵子树的根结点有且只有一个前驱,可以有0个或多个后继 因此,树是递归定义的。
在这里有一个要注意的点就是:在树形结构中,子树之间不能有交集,否则就不是树形结构。什么意思呢?例如B和C是A的子树,而在树形结构中,它们不能有任何交集,类似于:
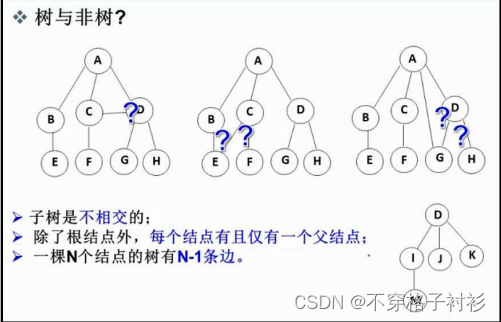
如果一个树形结构的字树相交的话,这个结构就不能称之为树形结构。
2.树的相关概念
这里有一张图,我们接下来关于树的各个概念都是围绕这张图展开的:
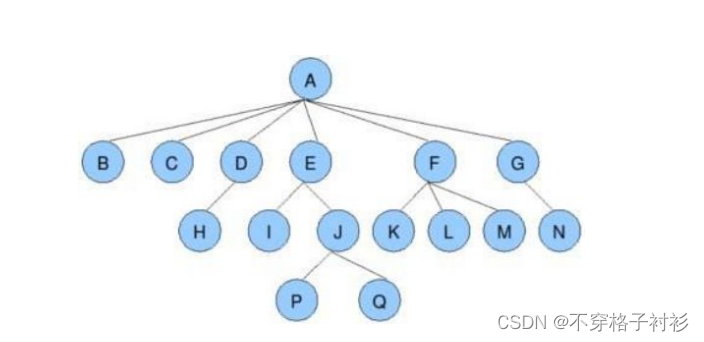
节点的度:一个结点含有的子树的个数称为该结点的度; 如上图:A的为6
叶结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I...等结点为叶结点,
简单来说,没有子节点的节点就被称为叶子节点。
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G...等结点为分支结点,
所以我们可以说一棵树是由所有分支节点加所有叶子节点组成的。
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
树的度:一棵树中,最大的结点的度称为树的度; 如上图:树的度为6,因为在这棵树中,度最大的结点是A,它有六个子节点,也是这棵树中子节点最多的结点,所以A的度就是这棵树的度。
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推;
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4

堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先,对于Q来说J,E,A是它的祖先
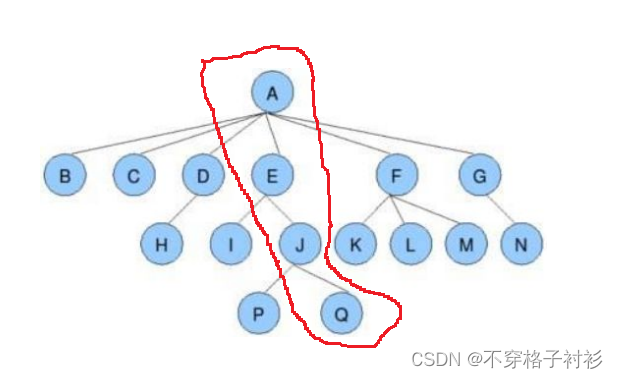
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林; 什么意思呢?只要有两棵及以上不相交的树,我们就可以将其称为森林。
3.树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既要保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法 等。我们在这里简单的介绍这些方法:
(1)直接表示法
使用直接表示法我们要先了解树的度,如果树的度是6,我们就要定义6个指针表示它们:
struct TreeNode
{int data;//数据struct TreeNode* child1;//指向孩子节点的指针struct TreeNode* child2;//...struct TreeNode* child6;}(2)双亲表示法
二十五双亲表示法比较简单,只要定义一个指向父节点的指针就可以:
struct TreeNode
{int data;struct TreeNode* parent;
}(3)左孩子右兄弟表示法
我们先将这种方法的表示写出来:
struct TreeNode
{int val;struct TreeNode* letfchild;struct TreeNode* rightbrother;
}“左孩子”表示这个指针只指向该结点的最左边的子结点,而它的子节点的“左孩子”也指向它自己最左边的子结点:
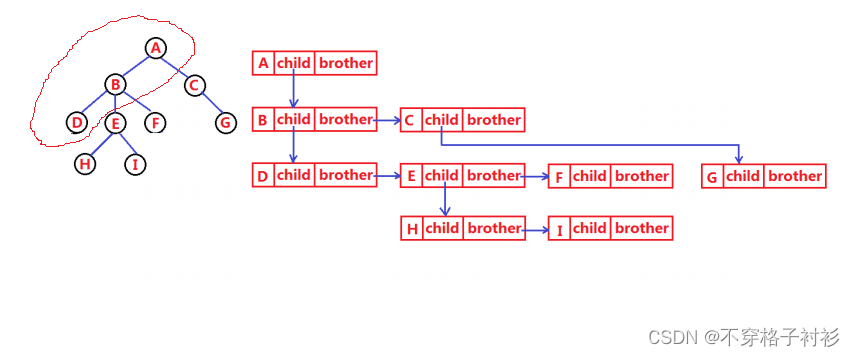
而它的“右兄弟”指针则向右边寻找兄弟结点,如果有兄弟结点,则指向它,然后继续向右找,直至右边找不到兄弟结点,“右兄弟”指针就指向空,这样一来,无论这棵树有多少子结点都可以用两个指针表示,“左孩子右兄弟”表示法也因其巧妙而被广泛使用。
4.树在实际中的运用(表示文件系统的目录树结构)
树在实际生活中出现得最多的场景就是在我们计算机中资源管理器文件系统的目录结构中,我们打开一个文件夹,里面有若干个文件,那么这个文件夹就是根结点,那若干个文件就是它的子结点:

怎么样,以这样的方式展开文件夹,它是不是就是我们数据结构中的树形结构呢。
相关文章:

数据结构——树的基础概念
目录 1.树的概念 2.树的相关概念 3.树的表示 (1)直接表示法 (2)双亲表示法 (3)左孩子右兄弟表示法 4.树在实际中的运用(表示文件系统的目录树结构) 1.树的概念 树是一种非线性的数据结构࿰…...

TimerManager和Timer
在RTSP服务器中需要一个定时器来定时发送音频帧和视频帧。音频帧每隔23ms发送一帧,视频帧每隔40ms发一帧。 因此需要两个定时器来定时发送,此时我们就需要用到一个TimerManager来管理Timer。 在TimerManager类中我们需要创建定时器文件描述符ÿ…...

手写Spring-MVC之前后置处理器与异常处理、数据库框架
Day48 手写Spring-MVC之前后置处理器与异常处理 前后置处理器 概念:从服务器获取的JSON数据可能是加密后的,因此服务端获取的时候需要进行解密(前置处理器)。 而从服务器传出的JSON数据可能需要加密,因此需要在处理返…...

学习笔记(linux高级编程)11
进程间通信 》信号通信 应用:异步通信。 中断,, 1~64;32应用编程。 如何响应: Term Default action is to terminate the process. Ign Default action is to ignore the signal. wait Core Default action is …...

vite+vue3+nginx配置统一公共前缀
方案1:重定向 server {listen 80;server_name localhost;location / {root /usr/share/nginx/html;index index.html;}location /music/ {proxy_pass http://127.0.0.1:80/;} }方案2:vitenginx双重配置 在方案1中,我们虽然能够实现 通过 …...

android 国内下载Gradle源
在中国使用 Gradle 时,可以配置使用一些国内的镜像源,以提高下载速度和稳定性。以下是几个常用的 Gradle 镜像源地址: 配置 gradle-wrapper.properties 文件: 阿里云: distributionUrlhttps\://services.gradle.org/distributions/gradle-7.…...
 拿走即用)
mysql8一键安装脚本(linux) 拿走即用
创建一个shell文件,将下面的代码放里面去,然后放到linux服务器上运行就可以了 #!/bin/bash#---------------------* # * # 2021-10-08 * # install mysql-8 * # * #---------------------*route=/usr #包存放路径 mys…...

C# 开发Winform DataGridView的增删改查实战
在C# WinForms应用程序中,DataGridView控件是一个非常强大的工具,用于显示和编辑表格数据。下面我将详细介绍如何在WinForm应用程序中使用DataGridView实现基本的数据库操作:增加、删除、修改和查询(CRUD)。 第一步&a…...

CentOS 7镜像列表服务下线,还想继续使用该怎么办?
目录 问题和解决方法 mirrorlist.centos.org 作用 vault.centos.org 作用 CentOS 7的生命周期已经在2024年6月30日终止(End of Life,EOL),官方将不再对该版本进行问题修复、功能更新以及其他形式的维护支持。这意味着使用 Cent…...

代码随想录训练营第二十八天 122买卖股票的最佳时间II 55跳跃游戏 45跳跃游戏II 1005K次取反后最大化的数组和
第一题: 原题链接:122. 买卖股票的最佳时机 II - 力扣(LeetCode) 思路: 这题十分简单,就是把相邻天数的金额相减,如果发现大于0就加到res中,返回res即可 代码如下: …...
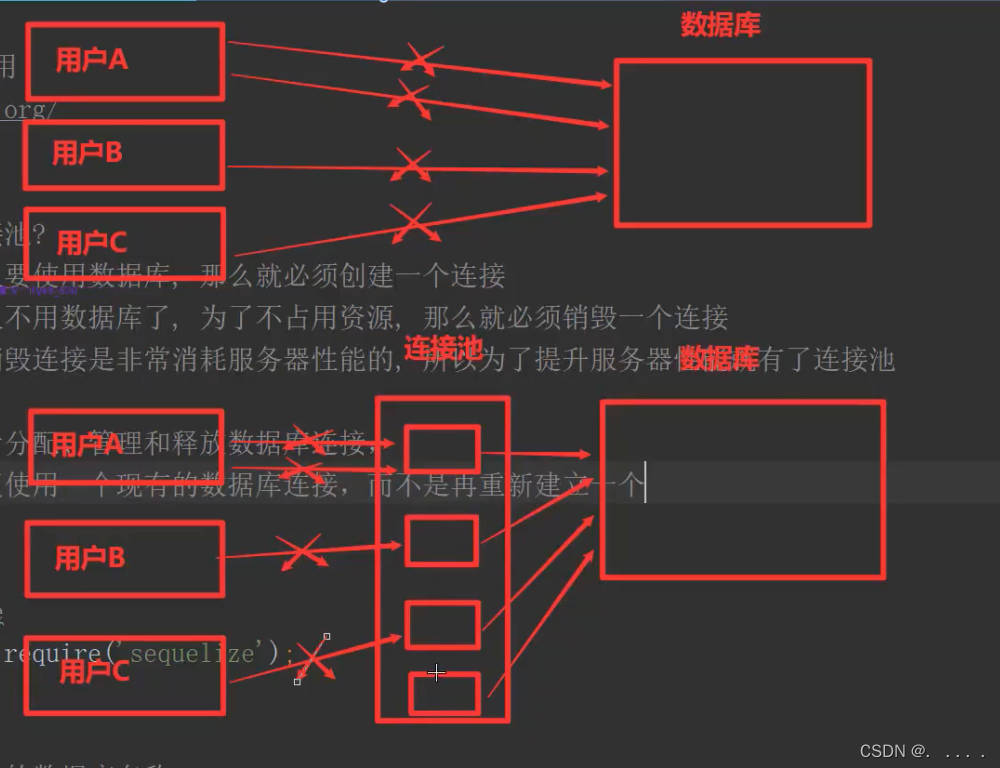
在node环境使用MySQL
什么是Sequelize? Sequelize是一个基于Promise的NodeJS ORM模块 什么是ORM? ORM(Object-Relational-Mapping)是对象关系映射 对象关系映射可以把JS中的类和对象,和数据库中的表和数据进行关系映射。映射之后我们就可以直接通过类和对象来操作数据表和数据了, 就…...

spdlog一个非常好用的C++日志库(四): 源码分析之logger类
目录 1.简介 2.类图关系 3.logger数据成员 4.logger函数成员 4.1.构造与析构 4.1.1.构造函数 4.1.2.拷贝构造、移动构造 4.2.交换操作 4.3.log()记录日志消息 4.3.1.格式串 4.3.2.普通字符串 4.3.3.日志级别 4.3.4.宽字符支持 4.4.sink_it_:将log消息…...
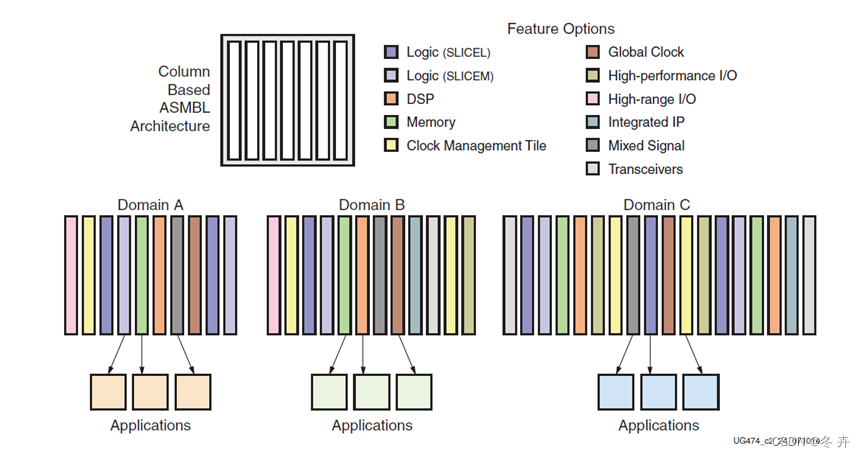
逻辑这回事(七)---- 器件基础
Xilinx FPGA创建了先进的硅模块(ASMBL)架构,以实现FPGA具有针对不同应用程序领域优化的各种功能组合的平台。通过这一创新,Xilinx提供了更多的设备选择,使客户能够为其特定设计选择具有正确的功能和功能组合的FPGA。ASMBL体系结构通过以下方式突破了传统的设计障碍:消除几…...

中俄汽车产业链合作前景广阔,东方经济论坛助力双边合作与创新
随着中国汽车零部件企业的竞争力和创新能力不断增强,中国汽车及零部件行业在俄罗斯的市场份额和品牌影响力显著提升,中俄两国在汽车产业链上的合作展现出巨大的潜力和广阔的前景。2024年5月,俄罗斯乘用车新车销量达到12.8万辆,同比…...

第六篇:精通Docker Compose:打造高效的多容器应用环境
精通Docker Compose:打造高效的多容器应用环境 1. 引言 1.1 目的与重要性 在现代软件开发中,随着应用程序的复杂性不断增加,传统的单一容器部署方式已无法满足需求。Docker Compose作为一种强大的工具,专门用于定义和运行多容器…...
C++视觉开发 一.OpenCV环境配置
一.OpenCV安装环境配置 1.OpenCV安装 (1)下载 官方下载链接:http://opencv.org/releases 这边选择需要的版本,我是在windows下的4.9.0。(科学上网下载很快,否则可能会有点慢) (2)安装 双击下…...
)
大数据面试题之Kafka(3)
目录 Kafka支持什么语义,怎么实现ExactlyOnce? Kafka的消费者和消费者组有什么区别?为什么需要消费者组? Kafka producer的写入数据过程? Kafka producer的ack设署 Kafka的ack机制,解决了什么问题? Kafka读取消息是推还是拉的模式?有什…...

视频监控平台web客户端的免密查看视频页:在PC浏览器上如何调试手机上的前端网页(PC上的手机浏览器的开发者工具)
目录 一、手机上做前端页面开发调试 1、背景 2、视频监控平台AS-V1000的视频分享页 3、调试手机前端页面代码的条件 二、手机端的准备工作 1、手机准备 2、手机的开发者模式 3、PC和手机的连接 (1)进入调试模式 (2)选择…...

力扣2488.统计中位数为 K 的子数组
力扣2488.统计中位数为 K 的子数组 等价转换 子数组为奇数 : 左小 右小 左大 右大 左小 – 左大 右大 – 右小 子数组为偶数 : 左小 右小 左大 右大 – 1 左小 – 左大 右大 – 右小 - 1提示中说明k为两数中左边那个 先从k的下标pos开始往左逆序…...
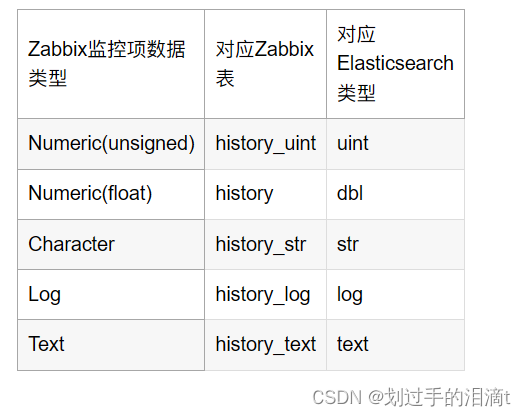
Zabbix对接Elasticsearch(ES)数据库(未成功)
0.需求分析 不管zabbix的后端数据库是oracle还是mysql,当zabbix监控的量级达到了一定程度后,那么对数据库的性能是一个非常严峻的挑战。特别是对历史数据的查询,将会变得非常非常的慢,别告诉我可以建索引优化,当量级达…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
