二刷力扣——单调栈

739. 每日温度

单调栈应该从栈底到栈顶 是递减的。

找下一个更大的 ，用递减单调栈，就可以确定在栈里面的每个比当前元素i小的元素，下一个更大的就是这个i，然后弹出并记录；然后当前元素i入栈，仍然满足递减要求。最后留在栈里面的是没有下一个更大的值的，符合要求。

找下一个更小的用递增单调栈同理。

result[被弹出下标]=使他弹出下标-被弹出下标。

复习一下Java集合知识：来自Java集合详解-CSDN博客

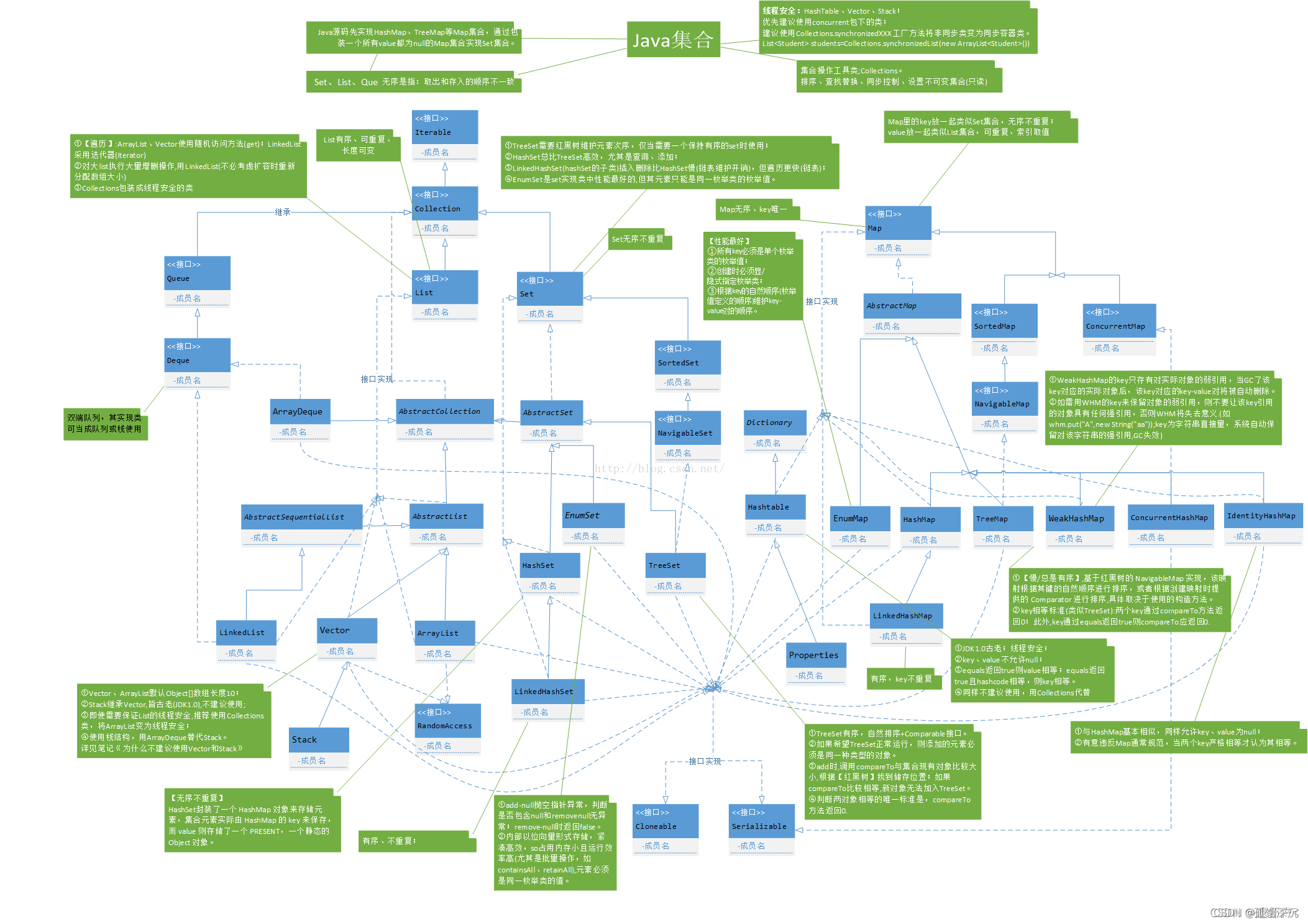
LinkedList 可以使用多种接口进行声明，包括但不限于：

• Deque 接口：Deque<Integer> deque = new LinkedList<>();: 双端队列的操作，包括栈和队列的功能。
• Queue 接口：Queue<Integer> queue = new LinkedList<>();: 适合实现队列的操作，包括 offer、poll、peek 等方法。
• List 接口：List<Integer> list = new LinkedList<>();: 通用的集合操作，如添加、删除、获取元素等。
• Collection 接口：Collection<Integer> collection = new LinkedList<>();: 这种声明方式表示通用的集合操作，适合需要简单地操作元素集合的场景。

class Solution {public int[] dailyTemperatures(int[] temperatures) {int n=temperatures.length;Deque<Integer> stack=new LinkedList<>();//放下标，int [] result =new int[n];for(int i=0;i<n;++i){int temp=temperatures[i];while(!stack.isEmpty() && temperatures[stack.peek()]<temp){int a=stack.pop();//小，被弹出result[a]=i-a;}//找到位置stack.push(i);}return result;}
}

时间、空间O(n)

496. 下一个更大元素 I

跟上一题区别是，先用单调栈把nums2处理，较小的元素弹出来的时候要找到当前元素i在nums1的位置，然后给到result。

这里不算下标而且数组里面没有重复元素，所以单调栈里面可以放元素值。

另外result一开始都赋值-1。最后可能nums1里有几个是没有下一个更大值的。

class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {int m=nums1.length ,n=nums2.length ;Deque<Integer> stack=new LinkedList<Integer>();int[] result=new int[m];HashMap<Integer,Integer> hash=new HashMap<>();// 放元素for(int i=0;i<m;++i){hash.put(nums1[i],i);}for(int i=0;i<m ;++i){result[i]=-1;}for(int i=0;i<n;++i){int tmp=nums2[i];while(!stack.isEmpty() && stack.peek()<tmp){int a=stack.pop();//被弹出的元素aint pos=hash.getOrDefault(a,-1);if(pos!=-1)result[pos]=tmp;}stack.push(tmp);}return result;}
}

时间是O(m+n)。初始化result和hash的是O(m)，单调栈循环是O(n)，因为用的HashMap，查找O(1)。

503. 下一个更大元素 II

要求循环地搜索元素的下一个更大的数，其实就是单调栈要走两次nums数组。

class Solution {public int[] nextGreaterElements(int[] nums) {int n=nums.length;int[] result=new int[n];Deque<Integer> stack=new LinkedList<>();Arrays.fill(result,-1);for(int j=0;j<2*n;++j){int i=j%n;int num=nums[i];while(!stack.isEmpty() && nums[stack.peek()]<num){int a=stack.pop();result[a]=nums[i];}stack.push(i);}return result;}
}

42. 接雨水

1、以列为单位，每列都找自己左边（包含自己）的最高柱子 l 和自己右边（包含自己）的最高柱子 r，就形成一个凹槽。然后每一列应该装下的雨水数就应该是（min(l , r) - 自己柱子高）*宽。所以主要关注l 和 r 怎么计算。

1.1、DP

维护一个lefts和rights数组，lefts[i]是l，rights[i]就是r。

那么递推公式就是：（min(lefts[i] , rights[i]) - 自己柱子高）*宽

关键得到这两个数组，还是很直观的，lefts涉及到的是i及左边的，所以从左往右递推；rights从右往左。

class Solution {public int trap(int[] height) {int n=height.length;int count=0;int[] lefts=new int[n];int[] rights=new int[n];lefts[0]=height[0];for(int i=1;i<n;++i){lefts[i]=Math.max(lefts[i-1],height[i]);}rights[n-1]=height[n-1];for(int i=n-2;i>=0;--i){rights[i]=Math.max(rights[i+1],height[i]);}for(int i=0;i<n;++i){count+=(Math.min(lefts[i],rights[i])-height[i]);}return count;}
}

时间空间：O（n）

1.2、双指针

用两个指针left、right从两端，逐渐逼近，逼近的判断条件是：left指向的和right指向的对比，哪一方小，就走一步。

①这里对于红框的判断不能理解，为什么当前的哪一方小，就能确定这一方的最大值更小呢？

下面这个说法很形象。其实就是A队B队比赛，遍历过了的都是输了的（或者平局的），假如B队的curB赢了A队的curA，所以目前MAX_B（其实就是curB）是目前两队最强。即A队最强的其实是输给B队过的了，所以A队最强不如B队最强。可以确定MAX_B=curB>MAX_A。A赢B就同理。

②又想：假如B队赢了A队，可以确定出现了一个凹槽：A队最高、curA、B队最高。这个凹槽的两端一定是我们要求的吗？

A队最高肯定是所要求的左边最高柱子l ，B队最高不一定是右边最高柱子 r。假如curA和curB之间还有比MAX_A更矮的柱子，压根不考虑因为我们是先找两端最高的，再在两个最高的里找最小的；假如有比MAX_B更高的柱子，那取Min值仍然还是MAX_A。A赢B就同理。

总的来说，哪一方输了，哪一方的输家就可以确定他的雨水了。决定这个雨水高度的就是他这一方的最强者（但是比另一方的最强者弱）。

可以用MAX_B>MAX_A，用height[a]<height[b]感觉更能体现这个“比赛”的过程吧，当前选手的大小。

class Solution {public int trap(int[] height) {int n=height.length;int a=0,b=n-1;//对手int MAX_A=0,MAX_B=0;//一个队里面已比对手的最强者int count=0;while(a<b){//更新最强者，要包括当前选手MAX_A=Math.max(MAX_A,height[a]);MAX_B=Math.max(MAX_B,height[b]);int yushui=0;//输的一方收集雨水if(height[a]<height[b])//b整体赢了{yushui=MAX_A-height[a];//注意凹槽两端a++;//输的下场，派下一个}else if(height[a]>=height[b]){yushui=MAX_B-height[b];b--;        }count+=yushui;}return count;}
}

时间O(n)空间O(1)

2、以行为单位

2.1 单调栈

以列为单位求，每个柱子的雨水是一次性求好，需要提前知道左边最高柱子和右边最高柱子，这形成凹槽1；

以行为单位求，是求以每个柱子为底的这一行能接的雨水，这一行雨水可以到的高度，应该是最接近自己的柱子的最小高度。即Min（上一个更大，下一个更大）。这是凹槽2。

这是按行求 和 按列求 的主要区别。

这一行，宽是 下一个更大和上一个更大的 下标间隔。高是Min值和中间 a 的差。

class Solution {public int trap(int[] height) {int n=height.length;int count=0;Deque<Integer> stack=new LinkedList<Integer> ();for(int i=0;i<n;++i){int tmp=height[i];while(!stack.isEmpty() && height[stack.peek()]<tmp)//凹槽{int a=stack.pop();//l=栈底，a，r=height[i]if(!stack.isEmpty()){int l=stack.peek();int r=i;int kuan=r-l-1;int gao=Math.min(height[l],height[r])-height[a];count+=kuan*gao;}}stack.push(i);}return count;}
}

84. 柱状图中最大的矩形