ubuntu 如何查看某一个网卡的ip地址
在Ubuntu中,你可以使用多种方法来查看某一个网卡的IP地址。以下是一些常用的方法:
-
使用
ip命令:ip命令是现代Linux系统中用于显示和操作路由、网络设备、策略路由和隧道的工具。要查看所有网络接口的IP地址,你可以使用:ip addr show如果你只想查看特定网卡的IP地址,比如
eth0,你可以使用:ip addr show eth0在输出中,查找
inet后面的地址,这就是该网卡的IP地址。 -
使用
ifconfig命令(可能需要安装net-tools包):虽然
ifconfig命令在现代Linux发行版中逐渐被ip命令所取代,但如果你习惯了使用ifconfig,你可以通过安装net-tools包来使用它。安装完成后,运行:ifconfig eth0将
eth0替换为你想要查看的网卡名称。在输出中,查找inet后面的地址来获取IP地址。 -
查看网络配置文件:
对于使用
netplan配置的Ubuntu系统(如Ubuntu 18.04及更高版本),你可以查看/etc/netplan/目录下的YAML配置文件来了解网络接口的静态配置。但请注意,这只能显示静态配置的IP地址,如果网卡是通过DHCP获取IP地址的,那么配置文件中可能不会有具体的IP地址。 -
使用
nmcli命令:如果你的Ubuntu系统上安装了NetworkManager,你可以使用
nmcli(NetworkManager的命令行界面)来查看网络接口的信息,包括IP地址。运行以下命令:nmcli device show eth0将
eth0替换为你要查看的网卡名称。在输出中,查找IP4.ADDRESS[1]后面的地址来获取IP地址。 -
查看
/sys/class/net/目录:你也可以直接从系统文件系统中读取网卡的信息。每个网络接口在
/sys/class/net/目录下都有一个对应的目录。你可以查看特定接口的address文件来获取网卡的MAC地址,但获取IP地址通常需要解析inet文件或使用其他方法。
通常,ip addr show命令是最直接和最常用的方法来查看网卡的IP地址。
相关文章:

ubuntu 如何查看某一个网卡的ip地址
在Ubuntu中,你可以使用多种方法来查看某一个网卡的IP地址。以下是一些常用的方法: 使用ip命令: ip命令是现代Linux系统中用于显示和操作路由、网络设备、策略路由和隧道的工具。要查看所有网络接口的IP地址,你可以使用:…...

跨界客户服务:拓展服务边界,创造更多价值
在当今这个日新月异的商业时代,跨界合作已不再是新鲜词汇,它如同一股强劲的东风,吹散了行业间的壁垒,为企业服务创新开辟了前所未有的广阔天地。特别是在客户服务领域,跨界合作正以前所未有的深度和广度,拓…...

linux驱动编程 - kfifo先进先出队列
简介: kfifo是Linux Kernel里面的一个 FIFO(先进先出)数据结构,它采用环形循环队列的数据结构来实现,提供一个无边界的字节流服务,并且使用并行无锁编程技术,即当它用于只有一个入队线程和一个出…...

JS 四舍五入使用整理
一、Number.toFixed() 把数字转换为字符串,结果的小数点后有指定位数的数字,重点返回的数据类型为字符串 toFixed() 方法将一个浮点数转换为指定小数位数的字符串表示,如果小数位数高于数字,则使用 0 来填充。 toFixed() 方法可把 Number 四舍五入为指定小数位数的数字。…...

上万组风电,光伏,用户负荷数据分享
上万组风电,光伏,用户负荷数据分享 可用于风光负荷预测等研究 获取链接🔗 https://pan.baidu.com/s/1izpymx6R3Y8JsFdx42rL0A 提取码:381i 获取链接🔗 https://pan.baidu.com/s/1izpymx6R3Y8JsFdx42rL0A 提取…...

在物联网快速发展的趋势下,Java 怎样优化对低功耗、资源受限的边缘设备的支持,保障物联网应用的稳定运行?
在物联网快速发展的趋势下,Java可以通过以下方式优化对低功耗、资源受限的边缘设备的支持,以保障物联网应用的稳定运行: 精简Java运行环境:针对边缘设备的资源限制,可以使用精简型的Java运行环境,避免不必要…...

java-HashSet 源码分析 1
## 深入分析 Java 中的 HashSet 源码 HashSet 是 Java 集合框架中的一个重要类,它基于哈希表实现,用于存储不重复的元素。HashSet 允许 null 元素,并且不保证元素的顺序。本文将详细分析 HashSet 的源码,包括其数据结构、构造方法…...

K8S 部署 EFK
安装说明 系统版本为 Centos7.9 内核版本为 6.3.5-1.el7 K8S版本为 v1.26.14 ES官网 开始安装 本次安装使用官方ECK方式部署 EFK,部署的是当前的最新版本。 在 Kubernetes 集群中部署 ECK 安装自定义资源 如果能打开这个网址的话直接用这个命令安装,打不开的话…...

AI Earth应用—— 在线使用sentinel数据VV和VH波段进行水体提取分析(昆明抚仙湖、滇池为例)
AI Earth 本文的主要目的就是对水体进行提取,这里,具体的操作步骤很简单基本上是通过,首页的数据检索,选择需要研究的区域,然后选择工具箱种的水体提取分析即可,剩下的就交给阿里云去处理,结果如下: 这是我所选取的一景影像: 详情 卫星: Sentinel-1 级别: 1 …...

基于Hadoop平台的电信客服数据的处理与分析③项目开发:搭建基于Hadoop的全分布式集群---任务9:HBase的安装和部署
任务描述 任务内容为HBase的安装部署与测试。 任务指导 HBase集群需要整个集群所有节点安装的HBase版本保持一致,并且拥有相同的配置 具体配置步骤如下: 1. 解压缩HBase的压缩包 2. 配置HBase的环境变量 3. 修改HBase的配置文件,HBase…...

go语言day09 通道 协程的死锁
Go语言学习——channel的死锁其实没那么复杂 - JackieZheng - 博客园 (cnblogs.com) 目录 通道 创建通道 1)无缓冲通道 2)有缓冲通道 通道的使用 1) 值从通道入口进 2) 值从通道出口出 信道死锁: 0)死锁现场0 1)死…...

黑马的ES课程中的不足
在我自己做项目使用ES的时候,发现了黑马没教的方法,以及一些它项目的小问题 搜索时的匹配方法 这个boolQuery().should 我的项目是通过文章的标题title和内容content来进行搜索 但是黑马它的项目只用了must 如果我们的title和content都用must&#x…...
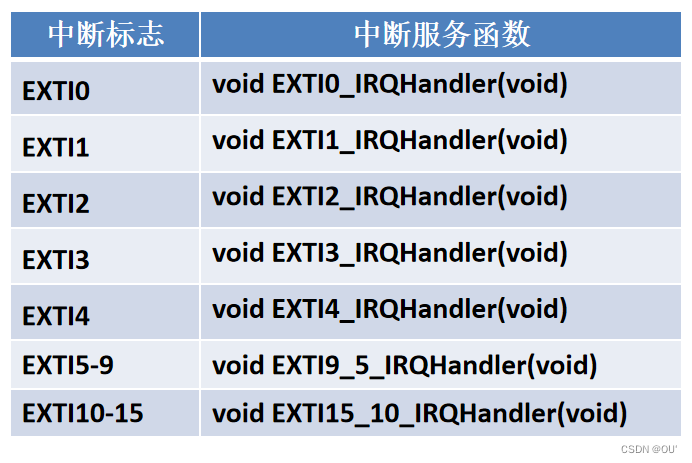
STM32 中断编程入门
目录 一、中断系统 1、中断的原理 2、中断类型 外部中断 定时器中断 DMA中断 3、中断处理函数 中断标志位清除 中断服务程序退出 二、实际应用 中断控制LED 任务要求 代码示例 中断控制串口通信 任务要求1 代码示例 任务要求2 代码示例 总结 学习目标&…...

使用maven搭建一个SpingBoot项目
1.首先创建一个maven项目 注意选择合适的jdk版本 2.添加依赖 2.在pom.xml中至少添加依赖 spring-boot-starter-web 依赖,目的是引入Tomcat,以及SpringMVC等,使项目具有web功能。 <!-- 引入 包含tomcat,SpringMVC,…...

使用 HTTPS 已成为网站的标配了
网站使用HTTPS的原因 背景:十年前,HTTPS并不普遍,但随着网络安全意识的提高,现在已成为网站标配。 网站升级到HTTPS的动机 安全问题:HTTP缺乏安全机制,易被窃取和篡改数据。例如,电信运营商劫…...

前后端分离Nginx
背景 旧的部署方式是将前端代码打包进后端包的resource server {listen 80;listen 443 ssl;server_name xxx.test.com;location / {proxy_pass http://xxx.test.com;} }后端:https:// xxx.test.com/simcard/querySimcard 前端:https:// x…...

【简单讲解下Tauri】
🌈个人主页: 程序员不想敲代码啊 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共…...

mac上挂载linux目录
在 macOS 上挂载 CentOS 目录步骤: 在挂载前确保 macOS 和 CentOS 在同一个局域网内,并且可以相互访问。如果有网络配置问题,可能会导致挂载失败或连接被拒绝的错误。 要在 macOS 上将 CentOS 的 /disk2/go 目录通过 NFS 挂载到 /Users/zon…...

Linux系统的服务——以Centos7为例
一、Linux系统的服务简介 服务是向外部提供对应功能的进程,其运行在系统后台,能够7*24小时持续不断的提供外界随时发来的服务请求,且服务进程常驻在内存中,具有固定的端口号,通过端口号就能找到服务内容。 提供服务的一…...

Numpy矩阵运算
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl Numpy概述 Numpy是Python的一个开源数值计算扩展库,主要用于存储和处理大型多维数组和矩阵,并且提供了大量的数学函数来操作这些数组。Numpy是Pytho…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
