订单折扣金额分摊算法|代金券分摊|收银系统|积分分摊|分摊|精度问题|按比例分配|钱分摊|钱分配
一个金额分摊的算法,将折扣分摊按比例(细单实收在总体的占比)到各个细单中。
此算法需要达到以下要求:
- 折扣金额接近细单总额,甚至折扣金额等于细单金额,某些时候甚至超过细单总额,要保证实收不为负数。
- 复杂度O(n)
…
写这个算法的初衷,就是因为现在网上的分摊算法,都没有考虑到最后一项不够减、只循环一次、折扣金额接近总额…
用例:
细单1:8.91
细单2:21.09
细单3:0.01
三个细单总和是 30.01
折扣金额:30
按比例分摊后,应该只有一项是 0.01
废话不多,直接上代码:
细单对象:
/*** 细单类*/@Datapublic static class Detail {/*** 用来标识记录*/private Long id;/*** 总额*/private BigDecimal money;}
分摊算法:(忽略了金额从小到大排序,后续补上)
/*** 分摊** @param detailList 细单* @param discountMoney 折扣* @return 新的细单集合*/public static List<Detail> allocateDiscountMoney(List<Detail> detailList, BigDecimal discountMoney) {// 分摊总金额BigDecimal allocatedAmountTotal = discountMoney;// 剩余分摊金额BigDecimal leftAllocatedAmount = allocatedAmountTotal;// 订单总实收BigDecimal orderTotalAmount = detailList.stream().map(Detail::getMoney).reduce(BigDecimal::add).orElse(BigDecimal.ZERO);// 结果集List<Detail> resultList = new ArrayList<>();for (int i = 0; i < detailList.size(); i++) {// 结果Detail resultDetail = new Detail();BeanUtils.copyProperties(detailList.get(i), resultDetail);BigDecimal money = resultDetail.getMoney();// 占比比例=自身实收/实收总额BigDecimal proportion = money.divide(orderTotalAmount, 10, RoundingMode.UP);// 分摊金额 = 总分摊金额*占比比例BigDecimal allocatedMoney = allocatedAmountTotal.multiply(proportion);// 折扣分摊金额向上取整,将精度差异提前吸收,此举使得最后一项足够吸收剩余折扣金额allocatedMoney = allocatedMoney.setScale(2, RoundingMode.UP);// 是否该订单最后一条商品 或者 已经不够分摊if (i == detailList.size() - 1 || leftAllocatedAmount.subtract(allocatedMoney).compareTo(BigDecimal.ZERO) <= 0) {allocatedMoney = leftAllocatedAmount;}// 防止订单金额负数(若最后一项执行此逻辑,则导致总金额有误)if (money.subtract(allocatedMoney).compareTo(BigDecimal.ZERO) < 0) {allocatedMoney = money;}// 单个商品分摊后的金额BigDecimal goodsActualMoneyAfterAllocated = money.subtract(allocatedMoney);// 累减已分摊金额leftAllocatedAmount = leftAllocatedAmount.subtract(allocatedMoney);resultDetail.setMoney(goodsActualMoneyAfterAllocated);resultList.add(resultDetail);}return resultList;}
测试类:
public static void main1() {List<Detail> detailList = new ArrayList<>();//Detail detail = new Detail();detail.setId(1L);detail.setMoney(new BigDecimal("8.91"));detailList.add(detail);//Detail detail2 = new Detail();detail2.setId(2L);detail2.setMoney(new BigDecimal("21.07"));detailList.add(detail2);//Detail detail3 = new Detail();detail3.setId(3L);detail3.setMoney(new BigDecimal("0.01"));detailList.add(detail3);System.out.println("分摊前:" + JSON.toJSONString(detailList));List<Detail> allocated = allocateDiscountMoney(detailList, new BigDecimal("30"));System.out.println("分摊后:" + JSON.toJSONString(allocated));}
问题:为什么每一项算分摊金额都是向上取整?
答:除最后一项外的每一项的折扣分摊算多了,最后一项就分摊得少,保证最后一项一定够分摊,前面的项在迭代时可以做金额如果不够分摊的兜底处理。而如果这么做,前面的不先兜底,后面的如果不够分摊是需要再往前找项来帮忙分摊的,复杂度就比较高。
~~
折扣金额的分摊,是反向的,其实正向的分摊也一并适用,并且逻辑是等价的。
例如:
细单1:8.91
细单2:21.09
细单3:0.01
三个细单总和是 30.01
折扣金额:30
我们也可以看做最终金额为 0.01,用0.01来分摊。
/*** 分摊** @param detailList 细单* @param tgtTotalMoney 待分摊的目标总金额* @return 新的细单集合*/public static List<Detail> allocateTgtTotalMoney(List<Detail> detailList, BigDecimal tgtTotalMoney) {// 分摊总金额BigDecimal allocatedAmountTotal = tgtTotalMoney;// 剩余分摊金额BigDecimal leftAllocatedAmount = allocatedAmountTotal;// 订单总实收BigDecimal orderTotalAmount = detailList.stream().map(Detail::getMoney).reduce(BigDecimal::add).orElse(BigDecimal.ZERO);// 结果集List<Detail> resultList = new ArrayList<>();for (int i = 0; i < detailList.size(); i++) {// 结果Detail resultDetail = new Detail();BeanUtils.copyProperties(detailList.get(i), resultDetail);BigDecimal money = resultDetail.getMoney();// 占比比例=自身实收/实收总额BigDecimal proportion = money.divide(orderTotalAmount, 10, RoundingMode.UP);// 分摊金额 = 总分摊金额*占比比例BigDecimal allocatedMoney = allocatedAmountTotal.multiply(proportion);// 折扣分摊金额向上取整,将精度差异提前吸收,此举使得最后一项足够吸收剩余折扣金额allocatedMoney = allocatedMoney.setScale(2, RoundingMode.UP);// 是否该订单最后一条商品 或者 已经不够分摊if (i == detailList.size() - 1 || leftAllocatedAmount.subtract(allocatedMoney).compareTo(BigDecimal.ZERO) <= 0) {allocatedMoney = leftAllocatedAmount;}// 累减已分摊金额leftAllocatedAmount = leftAllocatedAmount.subtract(allocatedMoney);resultDetail.setMoney(allocatedMoney);resultList.add(resultDetail);}return resultList;}
测试类:
public static void main2() {List<Detail> detailList = new ArrayList<>();//Detail detail = new Detail();detail.setId(1L);detail.setMoney(new BigDecimal("8.91"));detailList.add(detail);//Detail detail2 = new Detail();detail2.setId(2L);detail2.setMoney(new BigDecimal("21.07"));detailList.add(detail2);//Detail detail3 = new Detail();detail3.setId(3L);detail3.setMoney(new BigDecimal("0.01"));detailList.add(detail3);System.out.println("分摊前:" + JSON.toJSONString(detailList));List<Detail> allocated = allocateTgtTotalMoney(detailList, new BigDecimal("0.1"));System.out.println("分摊后:" + JSON.toJSONString(allocated));}
算法缺点(隐患):在折扣分摊的算法中,在需要保证每一项细单金额大于0的场景下,此算法需要谨慎使用,因为可能会把金额分摊为0元,但其实这也很难避免,因为总价30.01,折扣30,有很多项都会是0,只能说还有改进的空间,可以进行改动(例如向上取整)以保证在概率上出现0的情况少点。而且需要进行从小到大排序。
对你有帮助的话,点赞、收藏、评论、关注,谢谢各位大佬了~
相关文章:

订单折扣金额分摊算法|代金券分摊|收银系统|积分分摊|分摊|精度问题|按比例分配|钱分摊|钱分配
一个金额分摊的算法,将折扣分摊按比例(细单实收在总体的占比)到各个细单中。 此算法需要达到以下要求: 折扣金额接近细单总额,甚至折扣金额等于细单金额,某些时候甚至超过细单总额,要保证实收不…...

Matlab中collectPlaneWave函数的应用
查看文档如下: 可以看出最多5个参数,分别是阵列对象,信号幅度,入射角度,信号频率,光速。 在下面的代码中,我们先创建一个3阵元的阵列,位置为:(-1,0,0&#x…...

Linux系统的基础知识和常用命令
1、什么是Linux? 是一种免费使用和自由传播的类UNIX操作系统,其内核由林纳斯本纳第克特托瓦兹于1991年10月5日首次发布,它主要受到Minix和Unix思想的启发,是一个基于POSIX的多用户、多任务、支持多线程和多CPU的操作系统。它能运行…...

三相异步电动机的起动方法
1. 引言 2. 三相笼型异步电动机德起动方法 3. 三相绕线型异步电动机的起动方法 4. 软起动器起动 5. 参考文献 1 引言 三相异步电动机结构简单﹑价格低廉﹑运行可靠﹑维护方便,在工农业生产中得到了广泛应用。为使电动机能够转动起来,并很快达到工作转…...
)
【LinuxC语言】手撕Http协议之accept_request函数实现(一)
文章目录 前言accept_request函数作用accept_request实现解析方法根据不同方法进行不同操作http服务器响应格式unimplemented函数实现总结前言 在计算机网络中,HTTP协议是一种常见的应用层协议,它定义了客户端和服务器之间如何进行数据交换。在这篇文章中,我们将深入探讨Li…...
Redis Cluster 模式 的具体实施细节是什么样的?
概述 参考:What are Redis Cluster and How to setup Redis Cluster locally ? | by Rajat Pachauri | Medium Redis Cluster 的工作原理是将数据分布在多个节点上,同时确保高可用性和容错能力。以下是 Redis Cluster 运行方式的简要概述: …...

基于大模型的机器人控制
基于大模型的机器人控制是指利用深度学习中的大型神经网络模型来实现对机器人的精确控制。这种方法结合了深度学习的强大表征学习能力和机器人控制的实际需求,旨在提高机器人的自主性、灵活性和智能性。 基本原理 数据收集:首先,需要收集大量…...

在 PostgreSQL 中,如何处理数据的版本控制?
文章目录 一、使用时间戳字段进行版本控制二、使用版本号字段进行版本控制三、使用历史表进行版本控制四、使用 RETURNING 子句获取更新前后的版本五、使用数据库触发器进行版本控制 在 PostgreSQL 中,处理数据的版本控制可以通过多种方式实现,每种方式都…...

Rust 组织管理
Rust 组织管理 Rust 是一种系统编程语言,以其内存安全性、速度和并发性而闻名。它由 Mozilla 开发,并得到了一个庞大而活跃的社区的支持。Rust 的组织管理涉及多个方面,包括项目管理、社区参与、工具和库的维护,以及生态系统的整…...
vb.netcad二开自学笔记1:万里长征第一步Hello CAD!
已入门的朋友请绕行! 今天开启自学vb.net 开发autocad,网上相关资料太少了、太老了。花钱买课吧,穷!又舍不得,咬牙从小白开始摸索自学吧,虽然注定是踏上了一条艰苦之路,顺便作个自学笔记备忘!积…...

Vue的学习之数据与方法
前段期间,由于入职原因没有学习,现在已经正式入职啦,接下来继续加油学习。 一、数据与方法 文字备注已经在代码中,方便自己学习和理解 <!DOCTYPE html> <html><head><meta charset"utf-8">&l…...

刷题——在二叉树中找到最近公共祖先
在二叉树中找到两个节点的最近公共祖先_牛客题霸_牛客网 int lowestCommonAncestor(TreeNode* root, int o1, int o2) {if(root NULL) return -1;if((root->val o1) || (root->val o2)) return root->val;int left lowestCommonAncestor(root->left, o1, o2);i…...

nginx(三)—从Nginx配置熟悉Nginx功能
一、 Nginx配置文件结构 ... #全局块events { #events块... }http #http块 {... #http全局块server #server块{ ... #server全局块location [PATTERN] #location块{...}location [PATTERN] {...}}server{...}... #http全局块 …...

Python轮子:文件比较器——filecmp
原文链接:http://www.juzicode.com/python-module-filecmp filecmp模块可以用来比较文件或者目录。 安装和导入 filecmp是Python自带的模块,不需要额外安装,直接导入即可: import filecmp as fc #或者 import filecmp cmp()比较…...

uni-app组件 子组件onLoad、onReady事件无效
文章目录 导文解决方法 导文 突然发现在项目中,组件 子组件的onLoad、onReady事件无效 打印也出不来值 怎么处理呢? 解决方法 mounted() {console.log(onLoad, this.dateList);//有效// this.checkinDetails()},onReady() {console.log(onReady, this.da…...
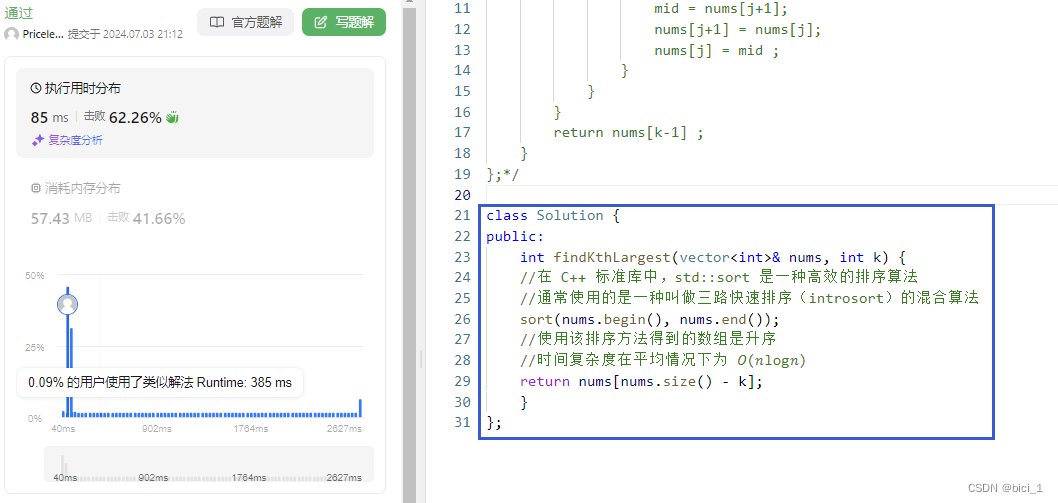
leetcode力扣_排序问题
215.数组中的第K个最大元素 鉴于已经将之前学的排序算法忘得差不多了,只会一个冒泡排序法了,就写了一个冒牌排序法,将给的数组按照降序排列,然后取nums[k-1]就是题目要求的,但是提交之后对于有的示例显示”超出时间限制…...

在 .NET 8 Web API 中实现弹性
在现代 Web 开发中,构建弹性 API 对于确保可靠性和性能至关重要。本文将指导您使用 Microsoft.Extensions.Http.Resilience 库在 .NET 8 Web API 中实现弹性。我们将介绍如何设置重试策略和超时,以使您的 API 更能抵御瞬时故障。 步骤 1.创建一个新的 .…...

linux下高级IO模型
高级IO 1.高级IO模型基本概念1.1 阻塞IO1.2 非阻塞IO1.3 信号驱动IO1.4 IO多路转接1.5 异步IO 2. 模型代码实现2.1 非阻塞IO2.2 多路转接-selectselect函数介绍什么才叫就绪呢?demoselect特点 2.3 多路转接-pollpoll函数介绍poll优缺点demo 2.4 多路转接-epoll&…...

掌握Mojolicious会话管理:构建安全、持久的Web应用
掌握Mojolicious会话管理:构建安全、持久的Web应用 Mojolicious是一个基于Perl的高性能、异步Web开发框架,它提供了一套完整的工具来构建现代Web应用。会话管理是Web开发中的一个关键组成部分,它允许应用识别和保持用户的登录状态。本文将深…...

24西安电子科技大学马克思主义学院—考研录取情况
01、马克思主义学院各个方向 02、24马克思主义学院近三年复试分数线对比 PS:马院24年院线相对于23年院线增加15分,反映了大家对于马克思主义理论学习与研究的热情高涨,也彰显了学院在人才培养、学科建设及学术研究等方面的不断进步与成就。 6…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
