代码随想录算法训练营第74天：路径总结[1]

代码随想录算法训练营第74天：路径总结

‍

A * 算法精讲 （A star算法）

卡码网：126. 骑士的攻击(opens new window)

题目描述

在象棋中，马和象的移动规则分别是“马走日”和“象走田”。现给定骑士的起始坐标和目标坐标，要求根据骑士的移动规则，计算从起点到达目标点所需的最短步数。

棋盘大小 1000 x 1000（棋盘的 x 和 y 坐标均在 [1, 1000] 区间内，包含边界）

输入描述

第一行包含一个整数 n，表示测试用例的数量。

接下来的 n 行，每行包含四个整数 a1, a2, b1, b2，分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。

输出描述

输出共 n 行，每行输出一个整数，表示骑士从起点到目标点的最短路径长度。

输入示例

6
5 2 5 4
1 1 2 2
1 1 8 8
1 1 8 7
2 1 3 3
4 6 4 6

输出示例

2
4
6
5
1
0

#思路

我们看到这道题目的第一个想法就是广搜，这也是最经典的广搜类型题目。

这里我直接给出广搜的C++代码：

#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
void bfs(int a1,int a2, int b1, int b2)
{queue<int> q;q.push(a1);q.push(a2);while(!q.empty()){int m=q.front(); q.pop();int n=q.front(); q.pop();if(m == b1 && n == b2)break;for(int i=0;i<8;i++){int mm=m + dir[i][0];int nn=n + dir[i][1];if(mm < 1 || mm > 1000 || nn < 1 || nn > 1000)continue;if(!moves[mm][nn]){moves[mm][nn]=moves[m][n]+1;q.push(mm);q.push(nn);}}}
}int main()
{
int n, a1, a2, b1, b2;
cin >> n;
while (n--) {
cin >> a1 >> a2 >> b1 >> b2;
memset(moves,0,sizeof(moves));bfs(a1, a2, b1, b2);cout << moves[b1][b2] << endl;}return 0;
}

提交后，大家会发现，超时了。

因为本题地图足够大，且 n 也有可能很大，导致有非常多的查询。

我们来看一下广搜的搜索过程，如图，红色是起点，绿色是终点，黄色是要遍历的点，最后从 起点 找到 达到终点的最短路径是棕色。

​​

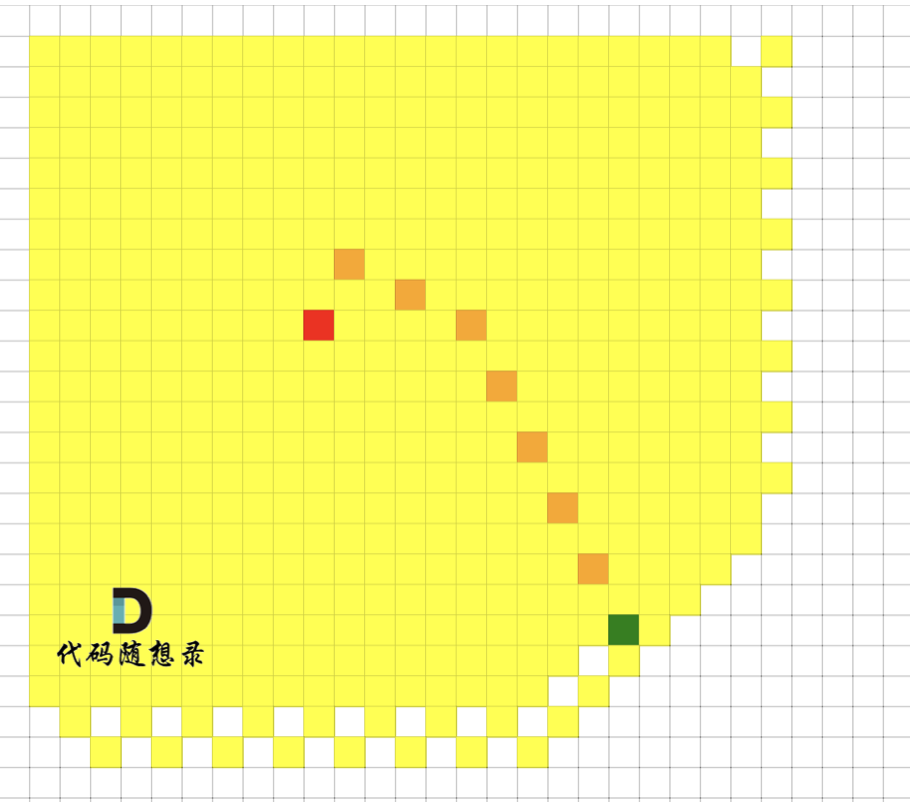
可以看出 广搜中，做了很多无用的遍历， 黄色的格子是广搜遍历到的点。

这里我们能不能让便利方向，向这终点的方向去遍历呢？

这样我们就可以避免很多无用遍历。

#Astar

Astar 是一种 广搜的改良版。 有的是 Astar是 dijkstra 的改良版。

其实只是场景不同而已 我们在搜索最短路的时候， 如果是无权图（边的权值都是1） 那就用广搜，代码简洁，时间效率和 dijkstra 差不多 （具体要取决于图的稠密）

如果是有权图（边有不同的权值），优先考虑 dijkstra。

而 Astar 关键在于 启发式函数， 也就是 影响 广搜或者 dijkstra 从 容器（队列）里取元素的优先顺序。

以下，我用BFS版本的A * 来进行讲解。

在BFS中，我们想搜索，从起点到终点的最短路径，要一层一层去遍历。

​​

如果 使用A * 的话，其搜索过程是这样的，如图，图中着色的都是我们要遍历的点。

​​

（上面两图中 最短路长度都是8，只是走的方式不同而已）

大家可以发现 **BFS 是没有目的性的 一圈一圈去搜索， 而 A *** 是有方向性的去搜索。

看出 A * 可以节省很多没有必要的遍历步骤。

为了让大家可以明显看到区别，我将 BFS 和 A * 制作成可视化动图，大家可以自己看看动图，效果更好。

地址：https://kamacoder.com/tools/knight.html

那么 A * 为什么可以有方向性的去搜索，它的如何知道方向呢？

其关键在于 启发式函数。

那么启发式函数落实到代码处，如果指引搜索的方向？

在本篇开篇中给出了BFS代码，指引 搜索的方向的关键代码在这里：

int m=q.front();q.pop();
int n=q.front();q.pop();

从队列里取出什么元素，接下来就是从哪里开始搜索。

所以 启发式函数 要影响的就是队列里元素的排序！

这是影响BFS搜索方向的关键。

对队列里节点进行排序，就需要给每一个节点权值，如何计算权值呢？

每个节点的权值为F，给出公式为：F = G + H

G：起点达到目前遍历节点的距离

F：目前遍历的节点到达终点的距离

起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。

本题的图是无权网格状，在计算两点距离通常有如下三种计算方式：

1. 曼哈顿距离，计算方式： d = abs(x1-x2)+abs(y1-y2)
2. 欧氏距离（欧拉距离） ，计算方式：d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
3. 切比雪夫距离，计算方式：d = max(abs(x1 - x2), abs(y1 - y2))

x1, x2 为起点坐标，y1, y2 为终点坐标 ，abs 为求绝对值，sqrt 为求开根号，

选择哪一种距离计算方式 也会导致 A * 算法的结果不同。

本题，采用欧拉距离才能最大程度体现 点与点之间的距离。

所以 使用欧拉距离计算 和 广搜搜出来的最短路的节点数是一样的。 （路径可能不同，但路径上的节点数是相同的）

我在制作动画演示的过程中，分别给出了曼哈顿、欧拉以及契比雪夫 三种计算方式下，A * 算法的寻路过程，大家可以自己看看看其区别。

动画地址：https://kamacoder.com/tools/knight.html

计算出来 F 之后，按照 F 的 大小，来选去出队列的节点。

可以使用 优先级队列 帮我们排好序，每次出队列，就是F最小的节点。

实现代码如下：（启发式函数 采用 欧拉距离计算方式）

#include<iostream>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
int b1, b2;
// F = G + H
// G = 从起点到该节点路径消耗
// H = 该节点到终点的预估消耗struct Knight{
int x,y;
int g,h,f;
bool operator < (const Knight & k) const{  // 重载运算符， 从小到大排序
return k.f < f;
}
};priority_queue<Knight> que;int Heuristic(const Knight& k) { // 欧拉距离
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号，这样可以提高精度
}
void astar(const Knight& k)
{
Knight cur, next;que.push(k);while(!que.empty()){cur=que.top(); que.pop();if(cur.x == b1 && cur.y == b2)break;for(int i = 0; i < 8; i++){next.x = cur.x + dir[i][0];next.y = cur.y + dir[i][1];if(next.x < 1 || next.x > 1000 || next.y < 1 || next.y > 1000)continue;if(!moves[next.x][next.y]){moves[next.x][next.y] = moves[cur.x][cur.y] + 1;// 开始计算Fnext.g = cur.g + 5; // 统一不开根号，这样可以提高精度，马走日，1 * 1 + 2 * 2 = 5
next.h = Heuristic(next);
next.f = next.g + next.h;
que.push(next);}}}
}int main()
{
int n, a1, a2;
cin >> n;
while (n--) {
cin >> a1 >> a2 >> b1 >> b2;
memset(moves,0,sizeof(moves));
Knight start;
start.x = a1;
start.y = a2;
start.g = 0;
start.h = Heuristic(start);
start.f = start.g + start.h;astar(start);
while(!que.empty()) que.pop(); // 队列清空cout << moves[b1][b2] << endl;}return 0;
}

#复杂度分析

A * 算法的时间复杂度 其实是不好去量化的，因为他取决于 启发式函数怎么写。

最坏情况下，A * 退化成广搜，算法的时间复杂度 是 O(n * 2)，n 为节点数量。

最佳情况，是从起点直接到终点，时间复杂度为 O(dlogd)，d 为起点到终点的深度。

因为在搜索的过程中也需要堆排序，所以是 O(dlogd)。

实际上 A * 的时间复杂度是介于 最优 和最坏 情况之间， 可以 非常粗略的认为 A * 算法的时间复杂度是 O(nlogn) ，n 为节点数量。

A * 算法的空间复杂度 O(b ^ d) ,d 为起点到终点的深度，b 是 图中节点间的连接数量，本题因为是无权网格图，所以 节点间连接数量为 4。

#拓展

如果本题大家使用 曼哈顿距离 或者 切比雪夫距离 计算的话，可以提交试一试，有的最短路结果是并不是最短的。

原因也是 曼哈顿 和 切比雪夫这两种计算方式在 本题的网格地图中，都没有体现出点到点的真正距离！

可能有些录友找到类似的题目，例如 poj 2243 ​**(opens new window)** ，使用 曼哈顿距离 提交也过了， 那是因为题目中的地图太小了，仅仅是一张 8 * 8的地图，根本看不出来 不同启发式函数写法的区别。

A * 算法 并不是一个明确的最短路算法，**A *** 算法搜的路径如何，完全取决于 启发式函数怎么写。

**A *** 算法并不能保证一定是最短路，因为在设计 启发式函数的时候，要考虑 时间效率与准确度之间的一个权衡。

虽然本题中，A * 算法得到是最短路，也是因为本题 启发式函数 和 地图结构都是最简单的。

例如在游戏中，在地图很大、不同路径权值不同、有障碍 且多个游戏单位在地图中寻路的情况，如果要计算准确最短路，耗时很大，会给玩家一种卡顿的感觉。

而真实玩家在玩游戏的时候，并不要求一定是最短路，次短路也是可以的 （玩家不一定能感受出来，及时感受出来也不是很在意），只要奔着目标走过去 大体就可以接受。

所以 在游戏开发设计中，**保证运行效率的情况下，A *** 算法中的启发式函数 设计往往不是最短路，而是接近最短路的 次短路设计。

大家如果玩 LOL，或者 王者荣耀 可以回忆一下：如果 从很远的地方点击 让英雄直接跑过去 是 跑的路径是不靠谱的，所以玩家们才会在 距离英雄尽可能近的位置去点击 让英雄跑过去。

#A * 的缺点

大家看上述 A * 代码的时候，可以看到 我们想 队列里添加了很多节点，但真正从队列里取出来的 仅仅是 靠启发式函数判断 距离终点最近的节点。

相对了 普通BFS，A * 算法只从 队列里取出 距离终点最近的节点。

那么问题来了，A * 在一次路径搜索中，大量不需要访问的节点都在队列里，会造成空间的过度消耗。

IDA * 算法 对这一空间增长问题进行了优化，关于 IDA * 算法，本篇不再做讲解，感兴趣的录友可以自行找资料学习。

另外还有一种场景 是 A * 解决不了的。

如果题目中，给出 多个可能的目标，然后在这多个目标中 选择最近的目标，这种 A * 就不擅长了， A * 只擅长给出明确的目标 然后找到最短路径。

如果是多个目标找最近目标（特别是潜在目标数量很多的时候），可以考虑 Dijkstra ，BFS 或者 Floyd。

最短路算法总结篇

至此已经讲解了四大最短路算法，分别是Dijkstra、Bellman_ford、SPFA 和 Floyd。

针对这四大最短路算法，我用了七篇长文才彻底讲清楚，分别是：

• dijkstra朴素版
• dijkstra堆优化版
• Bellman_ford
• Bellman_ford 队列优化算法（又名SPFA）
• bellman_ford 算法判断负权回路
• bellman_ford之单源有限最短路
• Floyd 算法精讲
• 启发式搜索：A * 算法

最短路算法比较复杂，而且各自有各自的应用场景，我来用一张表把讲过的最短路算法的使用场景都展现出来：

​​

（因为A * 属于启发式搜索，和上面最短路算法并不是一类，不适合一起对比，所以没有放在一起）

可能有同学感觉：这个表太复杂了，我记也记不住。

其实记不住的原因还是对 这几个最短路算法没有深刻的理解。

这里我给大家一个大体使用场景的分析：

如果遇到单源且边为正数，直接Dijkstra。

至于 使用朴素版还是 堆优化版 还是取决于图的稠密度， 多少节点多少边算是稠密图，多少算是稀疏图，这个没有量化，如果想量化只能写出两个版本然后做实验去测试，不同的判题机得出的结果还不太一样。

一般情况下，可以直接用堆优化版本。

如果遇到单源边可为负数，直接 Bellman-Ford，同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。

一般情况下，直接用 SPFA。

如果有负权回路，优先 Bellman-Ford， 如果是有限节点最短路 也优先 Bellman-Ford，理由是写代码比较方便。

如果是遇到多源点求最短路，直接 Floyd。

除非 源点特别少，且边都是正数，那可以 多次 Dijkstra 求出最短路径，但这种情况很少，一般出现多个源点了，就是想让你用 Floyd 了。

对于A * ，由于其高效性，所以在实际工程应用中使用最为广泛 ，由于其 结果的不唯一性，也就是可能是次短路的特性，一般不适合作为算法题。

游戏开发、地图导航、数据包路由等都广泛使用 A * 算法。

图论总结篇

从深搜广搜 到并查集，从最小生成树到拓扑排序， 最后是最短路算法系列。

至此算上本篇，一共30篇文章，图论之旅就在此收官了。

在0098.所有可达路径 ，我们接触了两种图的存储方式，邻接表和邻接矩阵，掌握两种图的存储方式很重要。

图的存储方式也是大家习惯在核心代码模式下刷题 经常忽略的 知识点。因为在力扣上刷题不需要掌握图的存储方式。

#深搜与广搜

在二叉树章节中，其实我们讲过了 深搜和广搜在二叉树上的搜索过程。

在图论章节中，深搜与广搜就是在图这个数据结构上的搜索过程。

深搜与广搜是图论里基本的搜索方法，大家需要掌握三点：

• 搜索方式：深搜是可一个方向搜，不到黄河不回头。 广搜是围绕这起点一圈一圈的去搜。
• 代码模板：需要熟练掌握深搜和广搜的基本写法。
• 应用场景：图论题目基本上可以即用深搜也可用广搜，无疑是用哪个方便而已

#注意事项

需要注意的是，同样是深搜模板题，会有两种写法。

在0099.岛屿的数量深搜.md 和 0105.有向图的完全可达性，涉及到dfs的两种写法。

我们对dfs函数的定义是 是处理当前节点 还是处理下一个节点 很重要，决定了两种dfs的写法。

这也是为什么很多录友看到不同的dfs写法，结果发现提交都能过的原因。

而深搜还有细节，有的深搜题目需要用到回溯的过程，有的就不用回溯的过程，

一般是需要计算路径的问题 需要回溯，如果只是染色问题（岛屿问题系列） 就不需要回溯。

例如： 0105.有向图的完全可达性 深搜就不需要回溯，而 0098.所有可达路径 中的递归就需要回溯，文章中都有详细讲解

注意：以上说的是不需要回溯，不是没有回溯，只要有递归就会有回溯，只是我们是否需要用到回溯这个过程，这是需要考虑的。

很多录友写出来的广搜可能超时了， 例如题目：0099.岛屿的数量广搜

根本原因是只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过。

具体原因，我在0099.岛屿的数量广搜 中详细讲了。

在深搜与广搜的讲解中，为了防止惯性思维，我特别加入了题目 0106.岛屿的周长，提醒大家，看到类似的题目，也不要上来就想着深搜和广搜。

还有一些图的问题，在题目描述中，是没有图的，需要我们自己构建一个图，例如 0110.字符串接龙，题目中连线都没有，需要我们自己去思考 什么样的两个字符串可以连成线。

#并查集

并查集相对来说是比较复杂的数据结构，其实他的代码不长，但想彻底学透并查集，需要从多个维度入手，

我在理论基础篇的时候 讲解如下重点：

• 为什么要用并查集，怎么不用个二维数据，或者set、map之类的。
• 并查集能解决那些问题，哪些场景会用到并查集
• 并查集原理以及代码实现
• 并查集写法的常见误区
• 带大家去模拟一遍并查集的过程
• 路径压缩的过程
• 时间复杂度分析

上面这几个维度 大家都去思考了，并查集基本就学明白了。

其实理论基础篇就算是给大家出了一道裸的并查集题目了，所以在后面的题目安排中，会稍稍的拔高一些，重点在于并查集的应用上。

例如 并查集可以判断这个图是否是树，因为树的话，只有一个根，符合并查集判断集合的逻辑，题目：0108.冗余连接。

在0109.冗余连接II 中 对有向树的判断难度更大一些，需要考虑的情况比较多。

#最小生成树

最小生成树是所有节点的最小连通子图， 即：以最小的成本（边的权值）将图中所有节点链接到一起。

最小生成树算法，有prim 和 kruskal。

prim 算法是维护节点的集合，而 Kruskal 是维护边的集合。

在 稀疏图中，用Kruskal更优。 在稠密图中，用prim算法更优。

边数量较少为稀疏图，接近或等于完全图（所有节点皆相连）为稠密图

Prim 算法 时间复杂度为 O(n^2)，其中 n 为节点数量，它的运行效率和图中边树无关，适用稠密图。

Kruskal算法 时间复杂度 为 O(nlogn)，其中n 为边的数量，适用稀疏图。

关于 prim算法，我自创了三部曲，来帮助大家理解：

1. 第一步，选距离生成树最近节点
2. 第二步，最近节点加入生成树
3. 第三步，更新非生成树节点到生成树的距离（即更新minDist数组）

大家只要理解这三部曲， prim算法 至少是可以写出一个框架出来，然后在慢慢补充细节，这样不至于 自己在写prim的时候 两眼一抹黑 完全凭感觉去写。

minDist数组 是prim算法的灵魂，它帮助 prim算法完成最重要的一步，就是如何找到 距离最小生成树最近的点。

kruscal的主要思路：

• 边的权值排序，因为要优先选最小的边加入到生成树里

• 遍历排序后的边

  • 如果边首尾的两个节点在同一个集合，说明如果连上这条边图中会出现环
  • 如果边首尾的两个节点不在同一个集合，加入到最小生成树，并把两个节点加入同一个集合

而判断节点是否在一个集合 以及将两个节点放入同一个集合，正是并查集的擅长所在。

所以 Kruskal 是需要用到并查集的。

这也是我在代码随想录图论编排上 为什么要先 讲解 并查集 在讲解 最小生成树。

#拓扑排序

拓扑排序 是在图上的一种排序。

概括来说，给出一个 有向图，把这个有向图转成线性的排序 就叫拓扑排序。

同样，拓扑排序也可以检测这个有向图 是否有环，即存在循环依赖的情况。

拓扑排序的一些应用场景，例如：大学排课，文件下载依赖 等等。

只要记住如下两步拓扑排序的过程，代码就容易写了：

1. 找到入度为0 的节点，加入结果集
2. 将该节点从图中移除

#最短路算法

最短路算法是图论中，比较复杂的算法，而且不同的最短路算法都有不同的应用场景。

我在 最短路算法总结篇 里已经做了一个高度的概括。

大家要时常温故而知新，才能透彻理解各个最短路算法。

#总结

到最后，图论终于剧终了，相信这是市面上大家能看到最全最细致的图论讲解教程。

图论也是我 《代码随想录》所有章节里 所费精力最大的一个章节。

只为了不负录友们的期待。 大家加油💪🏻