【机器学习】基于密度的聚类算法:DBSCAN详解


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 基于密度的聚类算法:DBSCAN详解
- 引言
- DBSCAN的基本概念
- 点的分类
- 聚类过程
- DBSCAN的参数
- DBSCAN的优势
- DBSCAN的局限性
- 实践案例
- 数据准备
- 应用DBSCAN
- 可视化结果
- 结论
基于密度的聚类算法:DBSCAN详解

引言
在数据科学和机器学习领域中,聚类是一种常见的无监督学习技术,用于发现数据集中的自然分组或结构。传统的聚类算法,如K-means,依赖于预定义的簇数量和球形簇假设,这限制了它们在复杂数据集上的表现。相比之下,基于密度的聚类算法,尤其是DBSCAN(Density-Based Spatial Clustering of Applications with Noise),能够识别任意形状的簇,并能有效地处理噪声点。本文将深入探讨DBSCAN的工作原理、参数选择、优势与局限性,以及其在实际应用中的表现。
DBSCAN的基本概念
点的分类
在DBSCAN中,数据点被分为三类:
- 核心点:在一个指定半径内(Eps)至少有MinPts个邻居点。
- 边界点:虽然它自身不是核心点,但位于某个核心点的Eps邻域内。
- 噪声点:既不是核心点也不是边界点。
聚类过程

DBSCAN从数据集中随机选取一个未访问的点开始,如果该点是核心点,则它和它的所有直接可达的点形成一个簇。如果一个点既不是核心点也不是边界点,则标记为噪声点。这一过程会重复进行,直到所有点都被访问过。
DBSCAN的参数
DBSCAN有两个关键参数:Eps(ε)和MinPts。
- Eps:定义了邻域的大小,即两个点被认为是“接近”的最大距离。
- MinPts:在Eps邻域内至少需要的点数来定义一个核心点。
正确选择这两个参数对于DBSCAN的成功至关重要。通常,Eps可以通过计算所有点之间的平均距离来估计,而MinPts则可以根据数据的维度和稀疏性来确定。
DBSCAN的优势
- 处理任意形状的簇:DBSCAN不需要簇具有球形或凸形,可以识别出任意形状的簇。
- 自动检测噪声:通过定义核心点和边界点,DBSCAN能够有效地识别并分离噪声点。
- 无需预定义簇的数量:与K-means等算法不同,DBSCAN不需要事先知道簇的数量。

DBSCAN的局限性
- 对参数敏感:不合适的Eps和MinPts值可能导致聚类效果不佳。
- 处理高维数据的挑战:在高维空间中,由于“维度灾难”,点之间的距离变得不那么有意义,导致DBSCAN性能下降。
- 对变量尺度敏感:特征之间的尺度差异可能会影响聚类结果。
实践案例
数据准备
首先,我们需要一个数据集。可以使用Python的scikit-learn库生成一个包含多个簇的数据集。
from sklearn.datasets import make_moons
X, _ = make_moons(n_samples=300, noise=0.05)
应用DBSCAN
使用sklearn.cluster.DBSCAN来应用算法。
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.3, min_samples=10).fit(X)
可视化结果
利用matplotlib库可视化聚类结果。
import matplotlib.pyplot as plt
plt.scatter(X[:,0], X[:,1], c=dbscan.labels_)
plt.show()
结论
DBSCAN作为一种基于密度的聚类算法,为处理复杂数据集提供了一种强大的工具。通过合理选择参数,它能够有效地识别数据中的自然分组,即使在存在噪声的情况下也能保持良好的性能。然而,其对参数的选择敏感性和在高维数据上的局限性也是在实际应用中需要注意的问题。
通过对DBSCAN的理解和应用,我们不仅能够更好地解析数据的内在结构,还能进一步探索数据科学领域的其他高级主题,如异常检测和模式识别。


相关文章:

【机器学习】基于密度的聚类算法:DBSCAN详解
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 基于密度的聚类算法:DBSCAN详解引言DBSCAN的基本概念点的分类聚类过…...

Qt 网络编程 网络信息获取操作
学习目标:网络信息获取操作 前置环境 运行环境:qt creator 4.12 学习内容 一、Qt 网络编程基础 Qt 直接提供了网络编程模块,包括基于 TCP/IP 的客户端和服务器相关类,如 QTcpSocket/QTcpServer 和 QUdpSocket,以及实现 HTTP、FTP 等协议的高级类,如 QNetworkRe…...

linux中的进程以及进程管理
程序和进程的区别和联系 程序(Program): 程序是一组指令的集合,通常存储在磁盘或其他存储设备上,是一种静态的概念。程序本身并没有运行,它只是一个可执行的文件或脚本,包含了一系列的指令和数…...
)
pyecharts可视化案例大全(11~20)
pyecharts可视化案例大全(11~20) 十一、设置动画效果十二、直方图带视觉组件十三、设置渐变色(线性渐变)十四、设置渐变色(径向渐变)十五、设置分割线十六、设置分隔区域十七、面积图十八、堆叠面积图十九、自定义线样式二十、折线图平滑处理十一、设置动画效果 在图表加载前…...

Docker在人工智能领域的应用与实战
摘要 人工智能(AI)技术的快速发展带来了对高效开发和部署工具的需求。Docker作为一个创新的容器化平台,为AI领域提供了强大的支持。本文详细介绍了Docker在AI模型开发、训练、部署以及服务器集群管理等方面的应用,并探讨了其在数…...

python基础篇(8):异常处理
在Python编程中,异常是程序运行时发生的错误,它会中断程序的正常执行流程。异常处理机制使得程序能够捕获这些错误,并进行适当的处理,从而避免程序崩溃。 1 错误类型 代码的错误一般会有语法错误和异常错误两种,语法错…...

FortiClient 用IPsec VPN 远程拨号到FortiGate说明文档
说明:本文档针对IPsec VPN 中的Remote VPN 进行说明,即远程用户使用PC中的FortiClient软件,通过VPN拨号的方式连接到公司总部FortiGate设备,访问公司内部服务器。在配置之前需要统一VPN策略和参数,如模式… 说明&#…...

Git-Unity项目版本管理
目录 准备GitHub新建项目并添加ssh密钥Unity文件夹 本文记录如何用git对unity 项目进行版本管理,并可传至GitHub远端。 准备 名称版本windows11Unity2202.3.9.f1gitN.A.githubN.A. GitHub新建项目并添加ssh密钥 GitHub新建一个repositorywindows11 生成ssh-key&…...

每日一题~ leetcode 402 (贪心+单调栈)
click me! 这个贪心的推导在leetcode上已经很明确了。 click me! 删除k个数,可以先考虑删除一个数。这也是一种常见的思路。(如果进行同样的操作多次,可以先只 考虑一次操作如何实现,或者他的影响。完成这一次操作后,…...
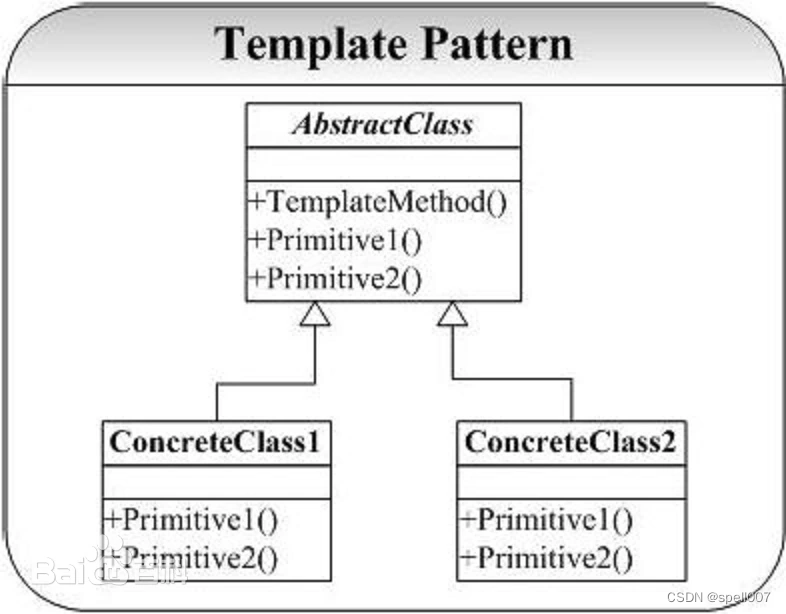
设计模式之模版方法
模版方法介绍 模版方法(Template Method)模式是一种行为型设计模式,它定义了一个操作(模板方法)的基本组合与控制流程,将一些步骤(抽象方法)推迟到子类中,使得子类可以在…...

docker部署redis/mongodb/
一、redis 创建/root/redis/conf/redis.conf 全部执行命令如下 docker run -it -d --name redis -p 6379:6379 --net mynet --ip 172.18.0.9 -m 400m -v /root/redis/conf:/usr/local/etc/redis -e TXAsia/Shangehai redis redis-server /usr/local/etc/redis/redis.conf 部署…...

LeetCode 581. 最短无序连续子数组
更多题解尽在 https://sugar.matrixlab.dev/algorithm 每日更新。 组队打卡,更多解法等你一起来参与哦! LeetCode 581. 最短无序连续子数组,难度中等。 排序 解题思路:首先对数组排序,然后找出两侧顺序的数组&#x…...
数据库可视化管理工具dbeaver试用及问题处理。
本文记录了在内网离线安装数据库可视化管理工具dbeaver的过程和相关问题处理方法。 一、下载dbeaver https://dbeaver.io/download/ 笔者测试时Windows平台最新版本为:dbeaver-ce-24.1.1-x86_64-setup.exe 二、安装方法 一路“下一步”即可 三、问题处理 1、问…...
)
29、php实现和为S的两个数字(含源码)
题目:php 实现 和为S的两个数字 描述: 输入一个递增排序的数组和一个数字S,在数组中查找两个数, 是的他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。 输出描述: 对应每个测…...

Spring Boot中的全局异常处理
Spring Boot中的全局异常处理 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中实现全局异常处理,这是保证应用…...

中英双语介绍美国苹果公司(Apple Inc.)
中文版 苹果公司简介 苹果公司(Apple Inc.)是一家美国跨国科技公司,总部位于加利福尼亚州库比蒂诺。作为全球最有影响力的科技公司之一,苹果以其创新的产品和设计引领了多个科技领域的变革。以下是对苹果公司发展历史、主要产品…...

C语言牢大坠机
目录 开头程序程序的流程图《牢大坠机》结尾 开头 大家好,我叫这是我58,今天,我们要来看关于牢大坠机的一些东西。 程序 #define _CRT_SECURE_NO_WARNINGS 1 #define HIGH 66 #include <stdio.h> #include <Windows.h> int ma…...

zdppy+vue3+antd 实现表格单元格编辑功能
初步实现 <template><a-button class"editable-add-btn" style"margin-bottom: 8px" click"handleAdd">Add</a-button><a-table bordered :data-source"dataSource" :columns"columns"><templa…...

elasticsearch索引怎么设计
Primary Shard(主分片) Primary Shard(主分片)是索引数据存储的基本单位,承担着数据写入和查询的职责。以下是关于Primary Shard的一些关键点: 1. 数据分布:每个索引在创建时会被分成多个主分…...

React 中 useState 和 useReducer 的联系和区别
文章目录 使用场景使用 useState使用 useReducer 联系区别用法状态更新逻辑适用场景可读性和可维护性 使用场景 使用 useState 状态逻辑简单。只涉及少量的状态更新。需要快速和简单的状态管理。 使用 useReducer 状态逻辑复杂。涉及多个子状态或多种状态更新逻辑。需要更好…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果