#### golang中【堆】的使用及底层 ####

 声明，本文部分内容摘自：

 Go: 深入理解堆实现及应用-腾讯云开发者社区-腾讯云

数组实现堆 | WXue

堆（Heap）是实现优先队列的数据结构，Go提供了接口和方法来操作堆。

应用

package mainimport ("container/heap""sort"
)/*
题目：给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字，滑动窗口每次只向右移动一位，返回滑动窗口中的最大值。示例：输入：nums = [1,3,-1,-3,5,3,6,7], k = 3输出：[3,3,5,5,6,7]解释：滑动窗口的位置                最大值---------------------------------[1 3  -1] -3  5  3  6  7       31 [3  -1  -3] 5  3  6  7       31  3 [-1  -3  5] 3  6  7       51  3  -1 [-3  5  3] 6  7       51  3  -1  -3 [5  3  6] 7       61  3  -1  -3  5 [3  6  7]      7
题解：大根堆可以帮助我们实时维护一系列元素中的最大值。初始时，我们将数组 nums 的前 k 个元素放入优先队列中。每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此，当我们后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。我们不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，我们可以在优先队列中存储二元组 (num,index)，表示元素 num 在数组中的下标为 index。
*/var a []int// heap 实现了标准库的heap.Interface接口
type hp struct {sort.IntSlice // type IntSlice []int
}func (h hp) Less(i, j int) bool {return a[h.IntSlice[i]] > a[h.IntSlice[j]]
}
func (h *hp) Push(v interface{}) {h.IntSlice = append(h.IntSlice, v.(int))
}
func (h *hp) Pop() interface{} {a := h.IntSlicev := a[len(a)-1]h.IntSlice = a[:len(a)-1]return v
}func maxSlidingWindow(nums []int, k int) (ans []int) {ans = make([]int, 1, len(nums)-k+1)a = nums// 初始化堆（优先队列）queue := &hp{make([]int, k)} // 优先队列for i := 0; i < k; i++ {queue.IntSlice[i] = i // 注意堆里存的是数组下标而非数组值，对应Less函数里的比较时需要a[h.IntSlice[i]]来比较值}heap.Init(queue) // 初始化+向下调整// 赋值ans[0]，因为不需要判断IntSlice[0]的元素是不是在边界外的左侧ans[0] = nums[queue.IntSlice[0]] // IntSlice[0] 下标为0=数组IntSlice的头部=堆顶元素// 窗口滑动for i := k; i < len(nums); i++ {heap.Push(queue, i)            // 入堆+向上调整for queue.IntSlice[0] <= i-k { // 判断IntSlice[0]的元素是不是在边界外的左侧heap.Pop(queue) // 出堆+向下调整}ans = append(ans, nums[queue.IntSlice[0]]) // IntSlice[0] 下标为0=数组头部=堆顶元素}return ans
}func main() {res := maxSlidingWindow([]int{1, 3, -1, -3, 5, 3, 6, 7}, 3)println(res)
}

底层

包：container/heap

接口：heap.Interface

源码：

type Interface interface {sort.InterfacePush(x interface{}) // 添加元素Pop() interface{}   // 弹出元素
}

其中，注意，实现heap.Interface接口需要嵌入sort.Interface，后者包含Len()、Less(i, j int) bool和Swap(i, j int)方法，用于确定元素间的排序。

全部源码：

type Interface interface {sort.InterfacePush(x any) // add x as element Len()Pop() any   // remove and return element Len() - 1.
}func Init(h Interface) {// heapifyn := h.Len()for i := n/2 - 1; i >= 0; i-- {down(h, i, n)}
}// Push pushes the element x onto the heap.
// The complexity is O(log n) where n = h.Len().
func Push(h Interface, x any) {h.Push(x)up(h, h.Len()-1)
}func Pop(h Interface) any {n := h.Len() - 1h.Swap(0, n)down(h, 0, n)return h.Pop()
}func Remove(h Interface, i int) any {n := h.Len() - 1if n != i {h.Swap(i, n)if !down(h, i, n) {up(h, i)}}return h.Pop()
}func Fix(h Interface, i int) {if !down(h, i, h.Len()) {up(h, i)}
}func up(h Interface, j int) {for {i := (j - 1) / 2 // parentif i == j || !h.Less(j, i) {break}h.Swap(i, j)j = i}
}func down(h Interface, i0, n int) bool {i := i0for {j1 := 2*i + 1if j1 >= n || j1 < 0 { // j1 < 0 after int overflowbreak}j := j1 // left childif j2 := j1 + 1; j2 < n && h.Less(j2, j1) {j = j2 // = 2*i + 2  // right child}if !h.Less(j, i) {break}h.Swap(i, j)i = j}return i > i0
}

其中：

    ① 初始化（Init）： 对一个未排序的切片构建堆。这是通过down方法实现的，down方法确保元素下沉到正确的位置，维持堆的性质。

    ② 添加元素（Push）： 元素被添加到切片的末尾，然后通过up方法上浮到正确的位置。

注意：标准库中的push函数中，第一行调用的【h.Push(x)】是上层业务代码中自行实现的heap.Interface的堆实例的push方法。

func Push(h Interface, x any) {
    h.Push(x)
    up(h, h.Len()-1)
}

    ③ 删除元素（Pop）： 堆顶元素（切片的第一个元素）被移动到切片末尾并返回，然后新的堆顶元素通过down方法恢复堆的性质。

    ④ 删除任意元素（Remove）： 类似Pop，但可以移除指定位置的元素。此操作需要综合up和down方法来调整堆。

    ⑤ 修改元素并调整堆（Fix）： 如果堆中某个元素被外部修改了（比如优先级改变），Fix方法会根据这个修改后的新值重新调整堆。

堆是一颗完全二叉树，可由数组表示

完全二叉树，逐层而下，从左到右，结点的位置完全由其序号觉得，因此可以用数组来实现。

计算各结点下标的公式，其中 𝑟𝑟 表示结点的下标，范围在 0 ~ n-1 之间，n 是二叉树结点的总数。

𝑃𝑎𝑟𝑒𝑛𝑡(𝑟)=⌊(𝑟−1)/2⌋𝑃𝑎𝑟𝑒𝑛𝑡(𝑟)=⌊(𝑟−1)/2⌋ 向下取整，当 𝑟≠0𝑟≠0 时

𝐿𝑒𝑓𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+1𝐿𝑒𝑓𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+1, 当 2𝑟+1<𝑛2𝑟+1<𝑛 时

𝑅𝑖𝑔ℎ𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+2𝑅𝑖𝑔ℎ𝑡𝑐ℎ𝑖𝑙𝑑(𝑟)=2𝑟+2, 当 2𝑟+2<𝑛2𝑟+2<𝑛 时

𝐿𝑒𝑓𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟−1𝐿𝑒𝑓𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟−1, 当 r 为偶数时

𝑅𝑖𝑔ℎ𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟+1𝑅𝑖𝑔ℎ𝑡𝑠𝑖𝑏𝑙𝑖𝑛𝑔()=𝑟+1 , 当 r 为奇数并且 𝑟+1<𝑛𝑟+1<𝑛 时

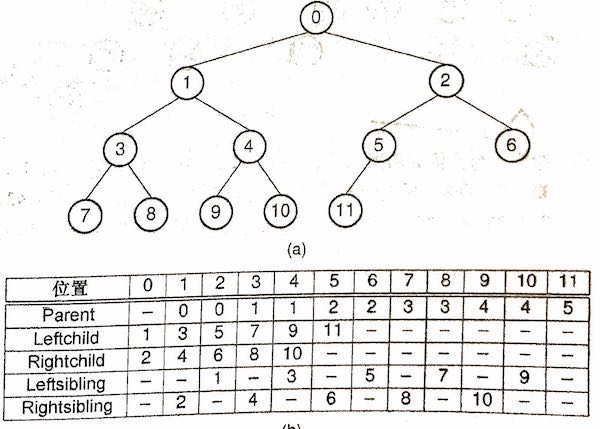
插入数值：在堆的末尾插入，然后不断向上提升，直到没有大小颠倒。

删除数值：首先把堆的最后一个节点的数值放到根上去，并且删除最后一个节点，然后不断向下交换直到没有大小颠倒为止。向下交换的时候如果 2 个儿子都比自己小，那么选择数值较小的儿子进行交换。

复杂度：建堆需要 On 的时间，但删除、插入都和树深度成正比，时间复杂度是 O𝑛𝑙𝑜𝑔𝑛。