集训 Day 2 模拟赛总结
复盘
7:30 开题
想到几天前被普及组难度模拟赛支配的恐惧,下意识觉得题目很难
先看 T1,好像不是很难,魔改 Kruskal 应该就行
看 T2 ,感觉很神奇,看到多串匹配想到 AC 自动机,又想了想 NOIP 模拟赛 T2 考 AC 自动机?奇奇怪怪
T3 神奇构造,先放
T4 想到以前做过的一道很像的题,记得是转化成二维平面中的点会很好做,但仔细想想发现不对
回来准备码 T1,推了推细节感觉问题不大,毕竟纯模拟 Kruskal 过程,大概 7:50 开始码
8:20 码完,测大样例发现跑 1.7s,时间限制 1.2s,? 仔细分析了一下,感觉这个思路很像正解,应该是哪个细节没处理好
尝试一行一行删代码,看那个地方跑得慢,发现竟然是 s o r t sort sort !逆天,想了想改成桶排,大样例极限跑 1.1s ,以为能过,就扔了
看 T2 ,首先看出有性质:包含别人的串没用。那么枚举左端点,找右端点最小的能匹配的串就行,这个 AC 自动机可以解决
接下来唐氏了一会,一直想把这 n n n 个串转化成若干个矩形,然后平面内扫描线?
去了个厕所,突然发现直接 for 一遍就做完了!回忆了一下 AC 自动机的细节 ,10:10 码完过了大样例
接下来看 T3 ,想到一个很显然但巨难写的做法,感觉很不对,决定放弃先看 T4
发现 40 40 40 是送的 ,枚举 x x x 即可,快速码
接下来看式子, h i ⌈ a i x ⌉ h_i\left \lceil \frac{a_i}{x} \right \rceil hi⌈xai⌉,意识到 后半部分得到变化是 s q r t sqrt sqrt 级的,想到对于 n ≤ 2000 n\leq 2000 n≤2000 可以把这些变化的点存起来
然发现数论分块会不了一点!不会找这些变化点
最后就在反复打表、猜性质,竟发现按 a i × h i a_i\times h_i ai×hi 排序后 x x x 有决策单调性?寄完了
最终 60 + 100 + 0 + 20 = 180 , rk_10086
总结一下,T1 应该再去拍一下的,或许能意识到时间上跑不过去的问题,赛后稍微卡一下常( vector<node> -> vector<int> ) 就过了
T3 构造实际上没那么难,应该多想想
T4 想的有点偏,对于 h i ⌈ a i x ⌉ h_i\left \lceil \frac{a_i}{x} \right \rceil hi⌈xai⌉ 结构应该优先考虑枚举 取整号内部的部分,这样是 O ( n l o g n ) O(nlogn) O(nlogn) 的,而不是数论分块的 n \sqrt n n
题解
T1

先说 K r u s k a l Kruskal Kruskal 做法
考虑暴力的情况:把所有边建出来,按权值从小到大排序
会发现枚举时会连着处理 一段本质上相同的边(连接同色点),考虑优化这个过程,直接 O ( 1 ) O(1) O(1) 算代价,同时需要注意标记 某颜色点内部是否连通
写的时候注意一下常数问题可以通过
接下来正解:
考虑最终状态,一定是每种颜色的连通块都至少往外连了一条边
那么对于每种颜色取出一个点,钦定这个点是往外连的,直接跑最小生成树
由于是完全图,考虑 P r i m Prim Prim,跑完后对于剩下的所有点,只需选择一个代价最小的颜色连上去即可,这一步可以直接把 P r i m Prim Prim 的 w w w 数组拿来用
#include<bits/stdc++.h>
using namespace std ;typedef long long LL ;
const int N = 5050 ; int n , a[N] ;
int x , y , l , h ;
// 完全图 prim
int c[N] , e[N][N] ;
bool vis[N] ;int main()
{scanf("%d" , &n ) ;for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &a[i] ) ;}scanf("%d%d%d%d" , &x , &y , &l , &h ) ;int C = 0 , A = 1 , B = 1 ;for(int i = 1 ; i <= n*n ; i ++ ) {C = (1LL*x*C+y)%h ;if( A <= B ) {e[A][B] = e[B][A] = C ;}B ++ ;if( B == n+1 ) {A ++ ;B = 1 ;}}LL ans = 0 ;for(int i = 1 ; i <= n ; i ++ ) c[i] = e[1][i] ;vis[1] = 1 ;for(int i = 1 ; i < n ; i ++ ) {int Min = 1e9 , id ;for(int j = 1 ; j <= n ; j ++ ) {if( !vis[j] && Min > c[j] ) {Min = c[j] ;id = j ;}}vis[id] = 1 ;ans += Min ;for(int j = 1 ; j <= n ; j ++ ) c[j] = min( c[j] , e[id][j] ) ;}for(int i = 1 ; i <= n ; i ++ ) ans += 1LL*c[i]*(a[i]-1) ;printf("%lld" , ans ) ;return 0 ;
}
T2
比较简单,放一个 AC 自动机的板子,回忆一下
char s[N] ;int tr[N*5][26] , tot , fail[N*5] , V[N*5] ;void Insert(){int p = 0 , len = strlen( s+1 ) ;for(int i = 1 ; i <= len ; i ++ ) {int c = s[i]-'a' ;if( !tr[p][c] ) tr[p][c] = ++tot , V[tot] = 1e9 ;p = tr[p][c] ;} V[p] = len ;}void AC_build(){queue<int> q ;for(int i = 0 ; i < 26 ; i ++ ) {if( tr[0][i] ) q.push( tr[0][i] ) ;}while( !q.empty() ) {int x = q.front() ; q.pop() ;for(int i = 0 ; i < 26 ; i ++ ) {if( tr[x][i] ) fail[tr[x][i]] = tr[fail[x]][i] , q.push( tr[x][i] ) , V[tr[x][i]] = min( V[tr[x][i]] , V[fail[tr[x][i]]] ) ;else tr[x][i] = tr[fail[x]][i] ;}}}
T3


T4

比较套路的题,应该会的
考虑 x x x 已知时,每个人的局数显然是 h i ⌈ a i x ⌉ h_i\left \lceil \frac{a_i}{x} \right \rceil hi⌈xai⌉
枚举 x x x 后再 check n n n 个人需要 n 2 n^2 n2 的复杂度,不可接受
( 赛时一直在想优化枚举 x x x 过程,但是 gg
考虑优化后半过程,在 x x x 一定时, 排好序后,对于一段 a i a_i ai, ⌈ a i x ⌉ \left \lceil \frac{a_i}{x} \right \rceil ⌈xai⌉ 的值是一定的,那么只维护段内最大与次大的 h i h_i hi
枚举 j = ⌈ a i x ⌉ j=\left \lceil \frac{a_i}{x} \right \rceil j=⌈xai⌉,合法的 a i a_i ai 范围可以算出来 [ x × ( j − 1 ) + 1 , x × j ] [x\times (j-1)+1,x\times j] [x×(j−1)+1,x×j] ,而且这样总复杂度是 O ( n l n ) O(nln) O(nln) 的
对于 h i h_i hi 简单的想法是 st 表维护,但有更好 (?) 的做法,直接维护 [ x × ( j − 1 ) + 1 , I N F ] [x\times (j-1)+1,INF] [x×(j−1)+1,INF] 后缀最大值,这样显然是对的,但要注意不要重算
这样加速了对于每个 x x x 找最大\次大值 的过程,可以通过本题
#include<bits/stdc++.h>
using namespace std ;typedef long long LL ;
const int N = 2e5+100 ; int T , n , a[N] , h[N] , Max ;
int Sm[N] , Sc[N] , id[N] ;
LL ans[N] ;int main()
{scanf("%d" , &T ) ;while( T -- ) {scanf("%d" , &n ) ;for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &h[i] ) ;}int Max = 0 ;memset( Sm , 0 , sizeof Sm ) ;memset( Sc , 0 , sizeof Sc ) ;for(int i = 1 ; i <= n ; i ++ ) {scanf("%d" , &a[i] ) ;Max = max( Max , a[i] ) ;if( h[i] > Sm[a[i]] ) {Sc[a[i]] = Sm[a[i]] ;Sm[a[i]] = h[i] ;id[a[i]] = i ;}else Sc[a[i]] = max( Sc[a[i]] , h[i] ) ;}for(int i = Max ; i >= 1 ; i -- ) {if( Sm[i+1] > Sm[i] ) {Sc[i] = Sm[i] ;Sm[i] = Sm[i+1] ;id[i] = id[i+1] ;}else Sc[i] = max( Sc[i] , Sm[i+1] ) ;Sc[i] = max( Sc[i] , Sc[i+1] ) ;}memset( ans , 0 , sizeof ans ) ;for(int x = 1 ; x <= Max ; x ++ ) {LL Mx = 0 , Cx = 0 ; int ID1 ;for(int j = 1 ; x*(j-1)+1 <= Max ; j ++ ) { // 每一段内找 h 最大/次大 即可 if( Mx < 1LL*Sm[x*(j-1)+1]*j ) {if( id[x*(j-1)+1] != ID1 ) Cx = Mx ;Mx = 1LL*Sm[x*(j-1)+1]*j ;ID1 = id[x*(j-1)+1] ;}else if( ID1 != id[x*(j-1)+1] ) {Cx = max( Cx , 1LL*Sm[x*(j-1)+1]*j ) ;}Cx = max( Cx , 1LL*Sc[x*(j-1)+1]*j ) ;}ans[ID1] = max( ans[ID1] , Mx-Cx ) ;}for(int i = 1 ; i <= n ; i ++ ) printf("%lld " , ans[i] ) ;printf("\n") ;}return 0 ;
}
相关文章:

集训 Day 2 模拟赛总结
复盘 7:30 开题 想到几天前被普及组难度模拟赛支配的恐惧,下意识觉得题目很难 先看 T1,好像不是很难,魔改 Kruskal 应该就行 看 T2 ,感觉很神奇,看到多串匹配想到 AC 自动机,又想了想 NOIP …...

Linux系统(CentOS)安装Mysql5.7.x
安装准备: Linux系统(CentOS)添加防火墙、iptables的安装和配置 请访问地址:https://blog.csdn.net/esqabc/article/details/140209894 1,下载mysql安装文件(mysql-5.7.44为例) 选择Linux通用版本64位(L…...

YModem在Android上的实现
(一)参考文献 【安卓相关】蓝牙基于Ymodem协议发送bin文件,对硬件设备进行升级。 - 简书当Android BLE遇上YModem - 简书 (二)收发机制 基于我们具体的需求,在原有的基础上加了一下前后的处理。 * MY YMO…...

循环练习题
代码: public static void main(String[] args) { for (char c1a;c1<z;c1){System.out.print(" "c1); }System.out.println();for (char c2Z;c2>A;c2--){System.out.print(" "c2);}} 结果为:...

Seata解决分布式事务
我举的例子是:在网上购物时,我们支付后,订单微服务会更新订单状态,同时会远程调用购物车微服务清空购物车,和调用商品微服务完成商品库存减一。 我们曾经说的事务是只能在本微服务完成回滚,意思就是如果过…...

C语言编译报错error: expected specifier-qualifier-list before
C语言编译报错 error: storage class specified for parameter error: expected specifier-qualifier-list before 原因: 报错信息 "expected specifier-qualifier-list" 通常表示编译器期望在某个地方出现类型指定列表,但却没有找到。这通常…...

无缝协作:如何实现VMware与Ubuntu虚拟机的剪切板共享!
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 剪贴板共享 📒📝 VMware设置📝 安装VMware Tools或open-vm-tools📝 验证剪贴板共享功能⚓️ 相关链接 🚓️📖 介绍 📖 无缝的剪贴板共享是提高工作效率的关键。在VMware和Ubuntu虚拟机的协同工作中,能够直接在宿…...

linux 进程堆栈分析
1.进程pid jsp -l | grep appName 或 ps -ef | grep appName 2.查看cpu top -c pidps -mp pid-o THREAD,tid,time / top -H -p pid #打印出进程对应的线程id及运行时间timeprintf %x\n 线程id3.查看gc jstat -gcutil | grep pid 500jstat -class pid4.查看进程日志 jsta…...

【续集】Java之父的退休之旅:从软件殿堂到多彩人生的探索
Java之父的退休之旅:从软件殿堂到多彩人生的探索-CSDN博客 四、科技领袖退休后的行业影响 4.1 传承与启迪 Gosling等科技领袖的退休,为行业内部年轻一代提供了更多的发展机会和成长空间。他们的退休不仅意味着权力和责任的交接,更是一种精…...

LVS+Nginx高可用集群---Nginx进阶与实战
1.Nginx中解决跨域问题 两个站点的域名不一样,就会有一个跨域问题。 跨域问题:了解同源策略:协议,域名,端口号都相同,只要有一个不相同那么就是非同源。 CORS全称Cross-Origin Resource Sharingÿ…...

Appium环境搭建,华为nova8鸿蒙系统(包括环境安装,环境配置)(一)
1.安装代码工具包 appium python client pip install appium-python-client 2.安装JDK 参考链接: antjmeterjenkins从0实现持续集成(Windows)-CSDN博客 3.下载并安卓SDK 下载地址:AndroidDevTools - Android开发工具 Android…...

【React】React18 Hooks 之 useReducer
目录 useReducer案例1:useReducer不带初始化函数案例2:useReducer带初始化函数注意事项1:dispatch函数不会改变正在运行的代码的状态注意事项2:获取dispatch函数触发后 JavaScript 变量的值注意事项3:触发了reducer&am…...

【cocos creator】2.4.x实现简单3d功能,点击选中,旋转,材质修改,透明材质
demo下载:(待审核) https://download.csdn.net/download/K86338236/89527924 const {ccclass, property } = cc._decorator;const enum box_color {NORMAL = 0,DASHED_LINE = 1,//虚线TRANSLUCENT = 2,//半透明 }@ccclass export default class main extends cc.Component {…...
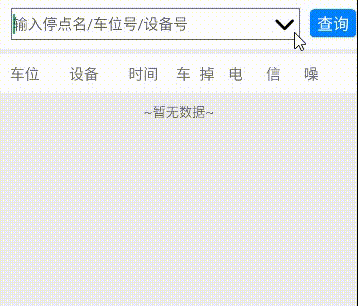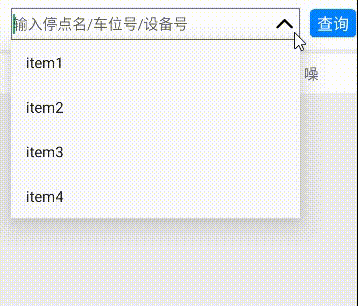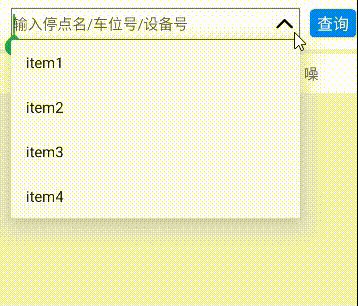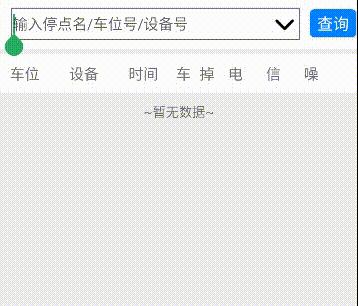
Android EditText+ListPopupWindow实现可编辑的下拉列表
Android EditTextListPopupWindow实现可编辑的下拉列表 📖1. 可编辑的下拉列表✅步骤一:准备视图✅步骤二:封装显示方法✅步骤三:获取视图并监听 📖2. 扩展上下箭头✅步骤一:准备上下箭头icon图标✅步骤二&…...

dify/api/models/task.py文件中的数据表
源码位置:dify/api/models/task.py CeleryTask 表结构 字段英文名数据类型字段中文名字备注idIntegerID自增主键,任务ID序列task_idString任务ID唯一任务标识statusString状态默认值为 PENDINGresultPickleType结果可为空date_doneDateTime完成日期默认…...

hdu物联网硬件实验3 按键和中断
学院 班级 学号 姓名 日期 成绩 实验题目 按键和中断 实验目的 实现闪灯功能转换 硬件原理 无 关键代码及注释 /* Button Turns on and off a light emitting diode(LED) connected to digital pin 13, when pressing a pushbutton attached…...

pytorch通过 tensorboardX 调用 Tensorboard 进行可视化
示例 import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader from torchvision import datasets, transformsfrom tensorboardX import SummaryWriter# 定义神经网络模型 class SimpleCNN(nn.Module):def __init__(self):…...

linux查看目录下的文件夹命令,find 查找某个目录,但是不包括这个目录本身?
linux查看目录下的文件夹命令,find 查找某个目录,但是不包括这个目录本身? Linux中查看目录下的文件夹的命令是使用ls命令。ls命令用于列出指定目录中的文件和文件夹。通过不同的选项可以实现显示详细信息、按照不同的排序方式以及使用不同的…...

单一设备上的 2 级自动驾驶:深入探究 Openpilot 的奥秘
Level 2 Autonomous Driving on a Single Device: Diving into the Devils of Openpilot 单一设备上的 2 级自动驾驶:深入探究 Openpilot 的奥秘 Abstract Equipped with a wide span of sensors, predominant autonomous driving solutions are becoming more m…...

向github远程仓库中push,要求使用token登录
Support for password authentication was removed on August 13, 2021. Please use a personal access token instead. 如上,当向github远程仓库push时,输入github的用户名和密码出现如上错误,要求使用token登录,此时只需要用户…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
