JavaScript 把CSDN博客内容存成PDF
F12 - 控制台 -命令行
- 输入执行:
允许粘贴 - 输入执行代码:
(function () {'use strict';var articleBox = $("div.article_content");articleBox.removeAttr("style");var head_str = "";var foot_str = "";var older = document.body.innerHTML;var title = document.getElementsByClassName('article-title-box')[0].innerHTML;var main_body = document.getElementsByClassName('article_content')[0].innerHTML;document.body.innerHTML = head_str + title + main_body + foot_str;$("#mainBox").width("100%");document.getElementsByTagName('body')[0].style.zoom = 0.8;window.print();document.body.innerHTML = older;return false;
})();
相关文章:

JavaScript 把CSDN博客内容存成PDF
F12 - 控制台 -命令行 输入执行:允许粘贴输入执行代码: (function () {use strict;var articleBox $("div.article_content");articleBox.removeAttr("style");var head_str "";var foot_str "";var older…...

uniapp——银行卡号脱敏
样式 代码 {{bankNumber.replace(/(\d{4})(?\d)/g, "●●●● ").replace(/(\d{2})(?\d{2}$)/, " $1")}} 将银行卡号按照每四位一组的方式进行处理,前面的变成 剩下的正常显示...

基于Spring Boot框架的EAM系统设计与实现
摘 要:文章设计并实现一个基于Spring Boot框架的EAM系统,以应对传统人工管理模式存在的低效与信息管理难题。系统利用Java语言、JSP技术、MySQL数据库等技术栈,构建了一个B/S架构的高效管理平台,提升了资产管理的信息化水平。该系…...

不同编程范式中作用域和闭包概念概述
不同编程范式中作用域和闭包概念概述 作用域(Scope)是指变量或函数在程序中的可见性和生命周期范围。它决定了哪些部分的代码可以访问某个变量或函数。在所有编程语言中都用于管理变量和函数的可见性范围,但不同语言可能有不同的作用域级别和…...
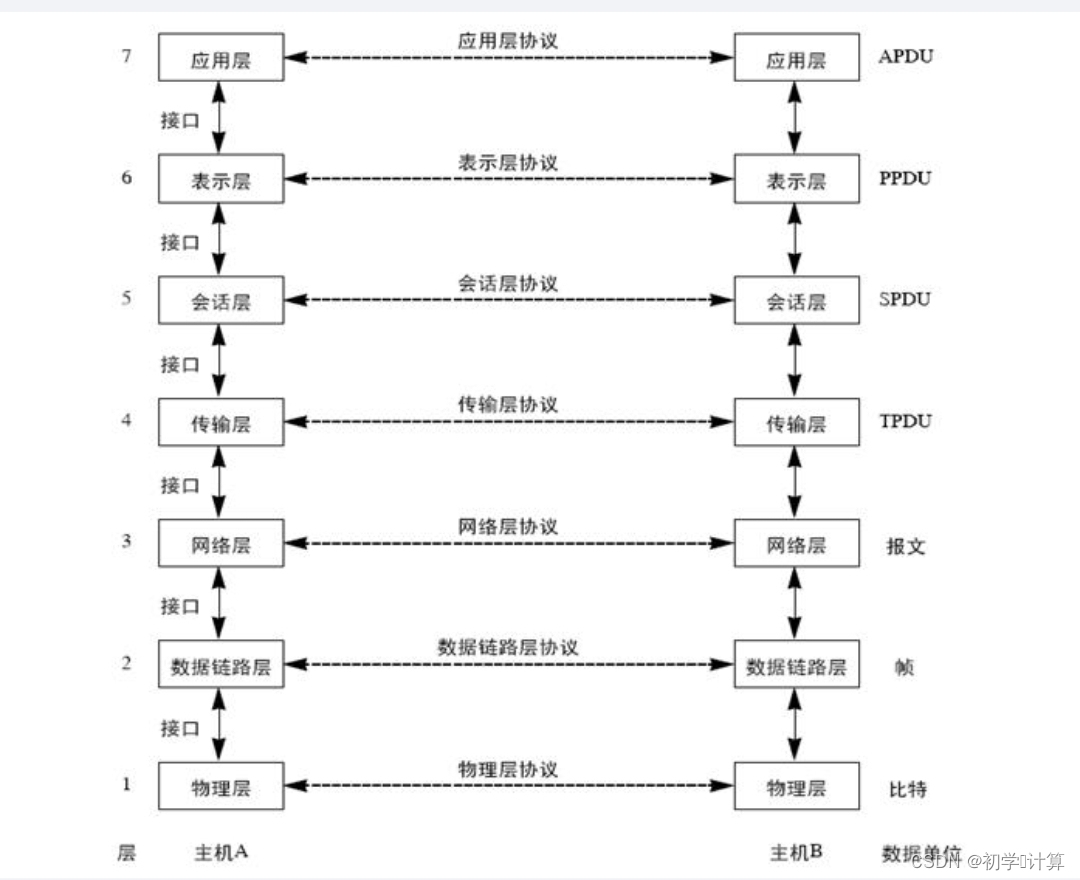
ISO/OSI七层模型
ISO:国际标准化/ OSI:开放系统互联 七层协议必背图 1.注意事项: 1.上三层是为用户服务的,下四层负责实际数据传输。 2.下四层的传输单位: 传输层; 数据段(报文) 网络层: 数据包(报…...

Golang | Leetcode Golang题解之第226题翻转二叉树
题目: 题解: func invertTree(root *TreeNode) *TreeNode {if root nil {return nil}left : invertTree(root.Left)right : invertTree(root.Right)root.Left rightroot.Right leftreturn root }...
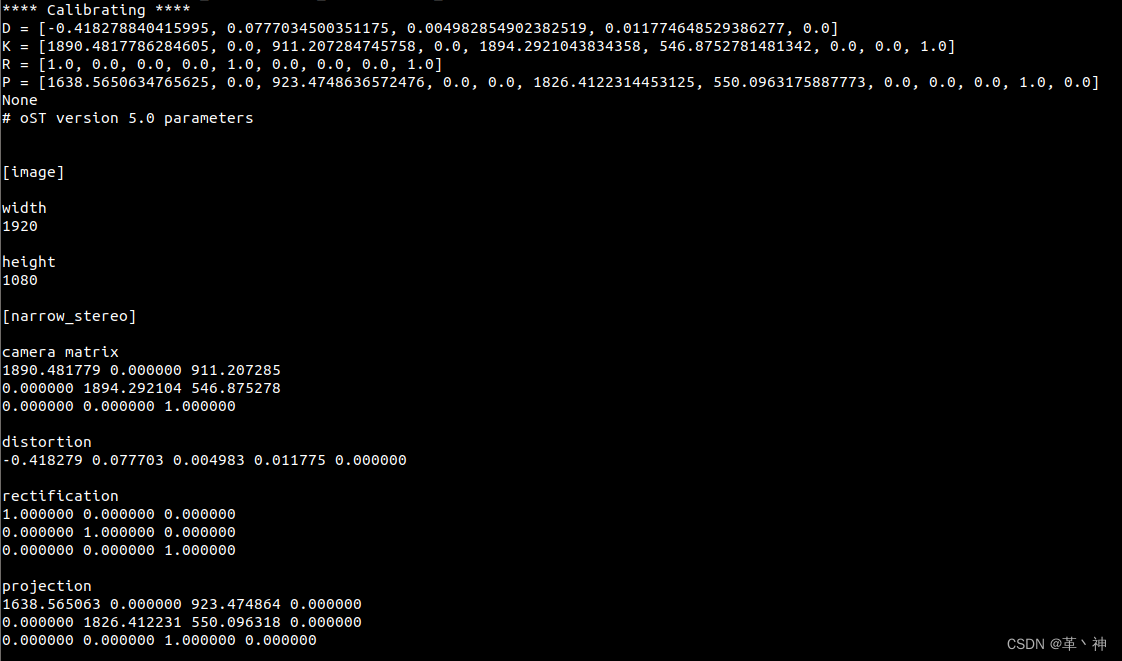
传感器标定(一)摄像头内参标定
一、使用ROS进行手动标定安装 1、安装 image-view &usb_cam ⽤于驱动相机 sudo apt-get install ros-melodic-image-view sudo apt-get install ros-melodic-usb-cam2、查看系统视频设备 v4l2- ctl -d /dev/video0 --all 查询所有相机具体的参数包括width和height ls /…...

基于门控循环单元 GRU 实现股票单变量时间序列预测(PyTorch版)
前言 系列专栏:【深度学习:算法项目实战】✨︎ 涉及医疗健康、财经金融、商业零售、食品饮料、运动健身、交通运输、环境科学、社交媒体以及文本和图像处理等诸多领域,讨论了各种复杂的深度神经网络思想,如卷积神经网络、循环神经网络、生成对…...

Apache tika 实现各种文档内容解析
Apache tika 实现各种文档内容解析 1、依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"…...

Vue3 监听属性
Vue3 监听属性 Vue.js 是一个流行的前端框架,以其响应式系统和组件化开发而闻名。在 Vue3 中,监听属性(Watchers)是一个核心功能,允许开发者监控和响应数据的变化。本文将详细介绍 Vue3 中监听属性的使用方法、场景和最佳实践。 监听属性的基本概念 在 Vue3 中,监听属…...

Transformer模型论文解读、源码分析和项目实践
本文是ChatGPT系列的开篇之作,为什么吧Transformer放到这里呢,因为不管是chatgpt-1, chatgpt-2, chatgpt-3都是以Transformer作为底层基础来实现,相当于chatgpt系列的老祖先了。如果想要深入的了解清楚chatgpt的来龙去…...

前端部署自动上传资源文件到cdn/oss 解决路由和访问慢的问题
参考文档:webpack-aliyun-oss-plugin - npm 安装依赖,这是一个预编译环境下的包 npm install webpack-aliyun-oss-plugin --save-dev 以下代码的意思是: webpack中引入一个oss上传插件,并且给予其初始参数,插件根据p…...

Diffusion 公式推导 2
Diffusion 公式推导 中对 DDPM 进行了推导,本文接着对 DDIM 进行推导。 目录 六. 模型改进 六. 模型改进 从扩散模型的推理过程不难看出,DDPM 有一个致命缺点 —— 推理速度过慢,因为逆扩散是从 x T x_{T} xT 到 x 0 x_{0} x0 的完整过…...

layui-表单(输入框)
1.基本使用方法 先写一个表单元素块 form 加上layui-form 里面写行区块结构,如下: 2.输入框样式选项 input框 placeholder默认文本 autocomplete自动填充 lay-verify required必填 3.下拉菜单样式选项 默认选择第一项 select框 disable禁…...

中职网络安全B模块渗透测试server2380
使用nmap扫描添加参数-sV Flag:2.4.38 添加参数-A不然扫不全 (这两题可以直接加-sV -A) Flag: 4.3.11-Ubuntu 根据nmap扫描发现系统为ubuntu系统,ubuntu操作系统在某些版本中默认包含一个名为"ubuntu"的用户帐户。这是为了方…...

微信小程序毕业设计-教育培训系统项目开发实战(附源码+论文)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...

【面试题】正向代理和反向代理的区别?
正向代理(Forward Proxy)和反向代理(Reverse Proxy)是两种常见的代理服务器类型,它们在网络通信中扮演着不同的角色,具有不同的功能和应用场景。 一、正向代理 1. 定义与位置 正向代理是位于客户端和目标…...

Python面试宝典第8题:二叉树遍历
题目 给定一棵二叉树的根节点 root ,返回它节点值的前序遍历。 示例 1: 输入:root [1,null,2,3] 输出:[1,2,3] 示例 2: 输入:root [] 输出:[] 示例 3: 输入:root […...

FastReport 指定sql 和修改 数据库连接地址的 工具类 :FastReportHelper
FastReport 指定sql 和修改 数据库连接地址的 工具类 :FastReportHelper 介绍核心代码:完整代码: 介绍 在FastReport中,经常会遇到需要给 sql 加条件的情况,或者给数据库地址做更换。 (废话不多说&#x…...

C++11中重要的新特性 Part one
序言 C11 是 C 编程语言的一个重要版本,于 2011 年由国际标准化组织 (ISO) 和国际电工委员会 (IEC) 旗下的 C 标准委员会 (ISO/IEC JTC1/SC22/WG21) 正式公布,并于同年 9 月出版。其正式名称为 ISO/IEC 14882:2011 - Information technology – Programm…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
