工业机床CNC设备如何上云?
工业机床CNC设备如何上云?
工业机床的计算机数控(CNC)设备实现远程监控数据上云,是现代制造业智能化转型的关键一环。这一过程不仅能够实时监测设备状态、优化生产流程,还能通过大数据分析提升生产效率与产品质量,实现预测性维护,减少停机时间。以下是实现这一目标的几个核心步骤和技术要点,旨在详细阐述其背后的原理与实施细节。
1. 数据采集与协议转换
首先,需在CNC设备上安装蓝蜂机床网关或利用已有的通信接口(如RS232、以太网等)。这些网关能够读取CNC控制器输出的状态信息、加工参数(如切削速度、进给率)、故障代码及运行时长等关键数据。

2. 安全的数据传输
数据从CNC设备传输到云端的过程中,确保数据的安全性和隐私保护至关重要。采用加密技术(如TLS/SSL)对传输数据进行加密,防止数据在传输过程中被截取或篡改。

3. 云端平台的选择
选择合适的工业物联网云平台作为数据接收与处理中心,如蓝蜂EMCP物联网云平台,这些平台通常提供丰富的机床控件来实现数据大屏展示,以及可以创建数据中心将多台设备的画面进行集中展示,实现数据汇总。创建自定义报表,实现日报月报年报的生成。支持多种报警方式,多终端展示,随时随地查看机床数据。

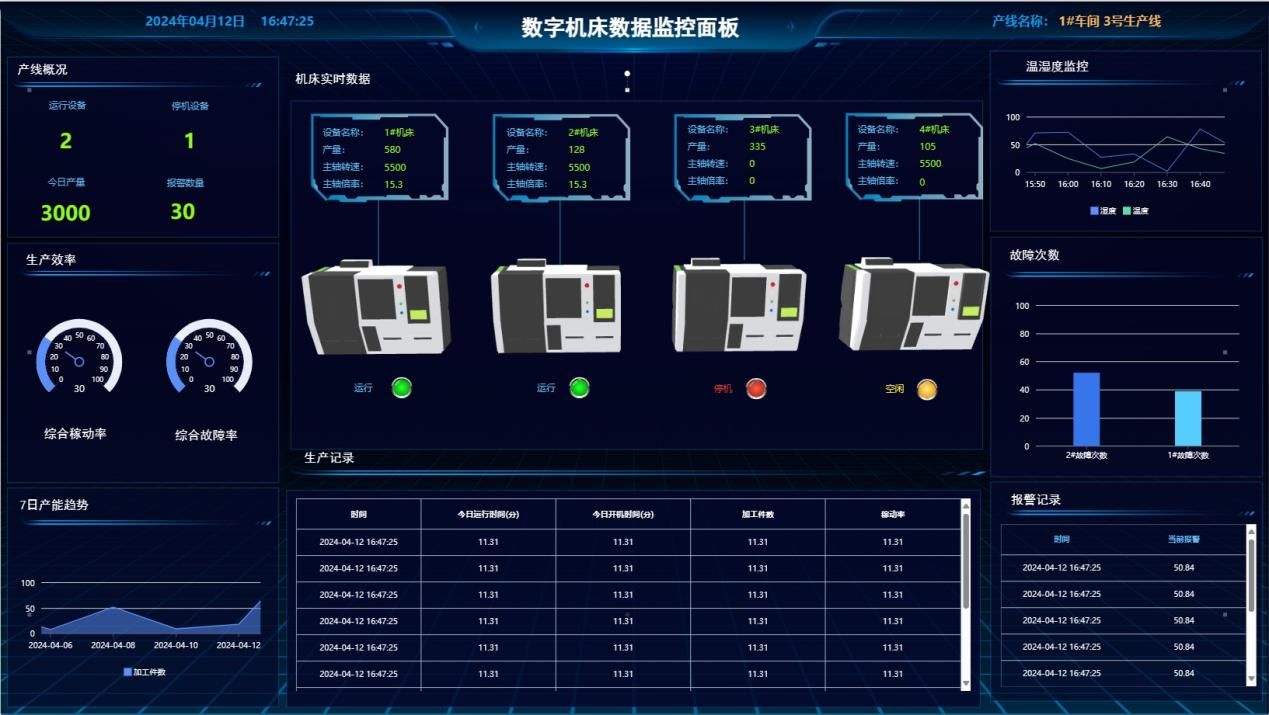
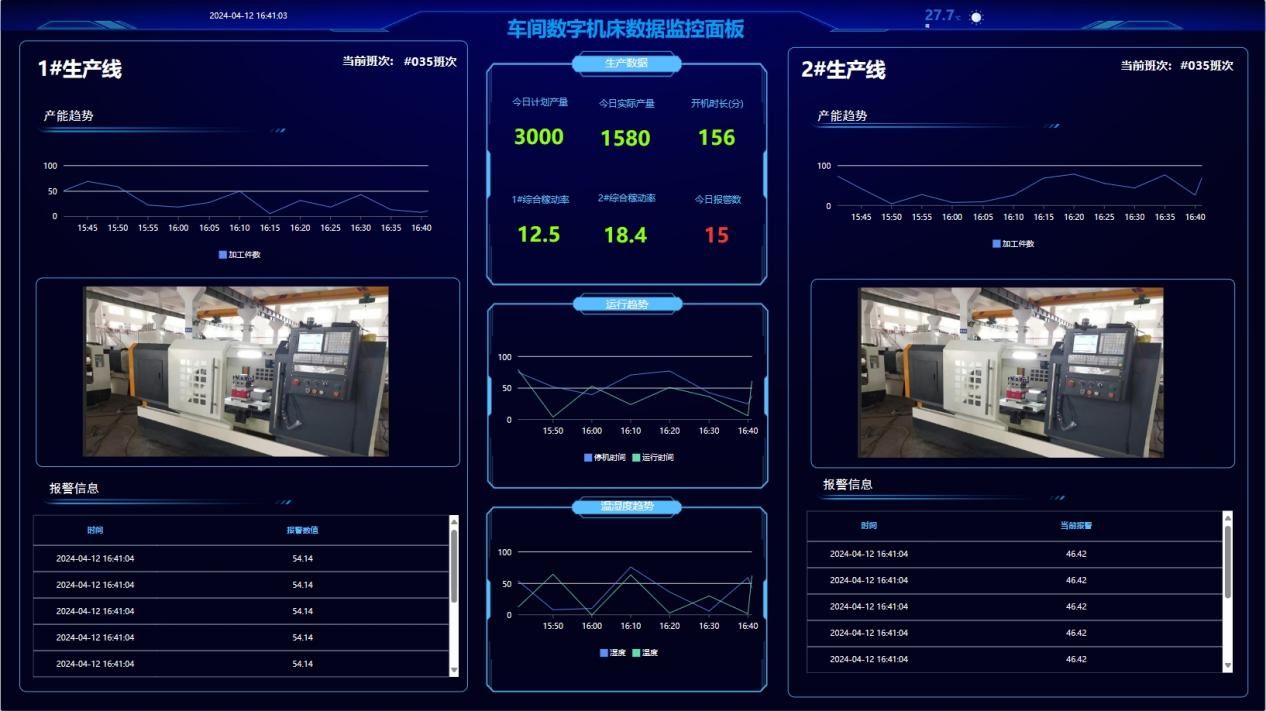
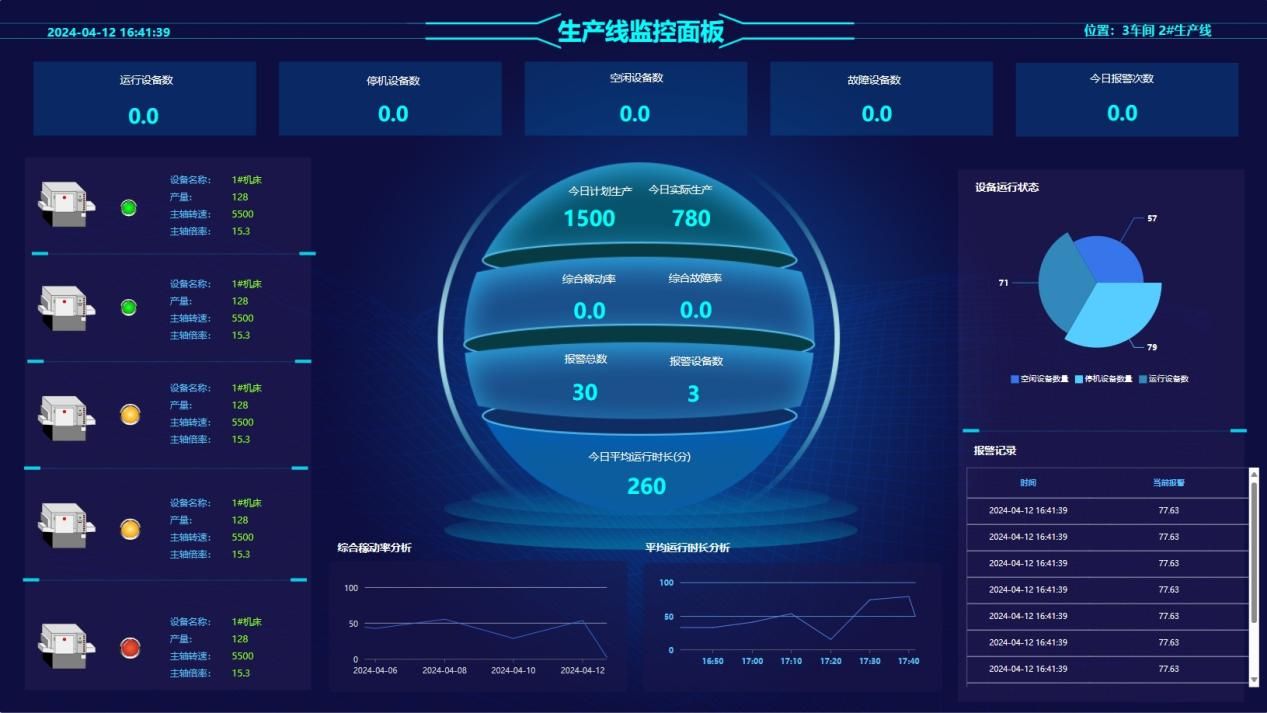
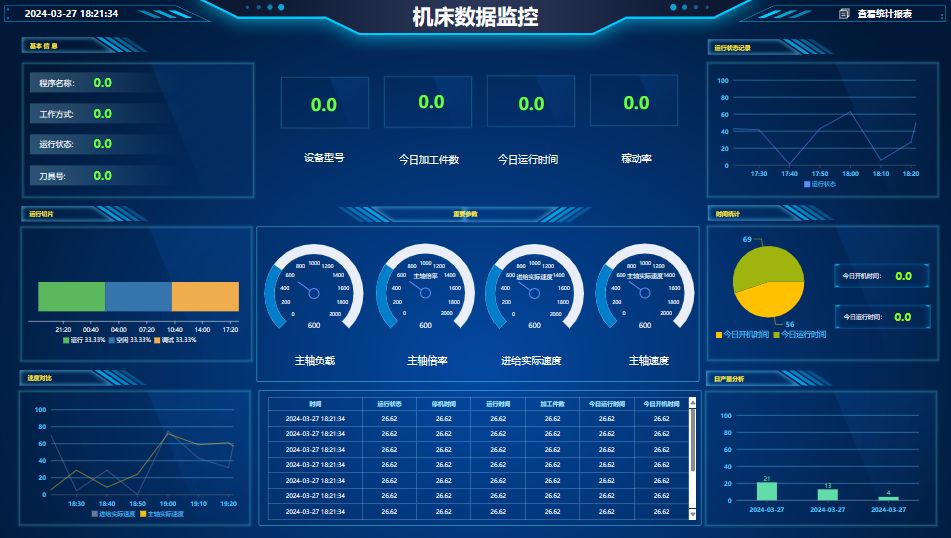
4. 数据处理与分析
一旦数据上云,即可利用云计算的强大能力进行实时数据分析与处理。这包括但不限于设备状态监控、性能指标分析、异常检测以及预测性维护模型的构建。通过机器学习算法,可以从历史数据中挖掘出设备故障的早期迹象,提前安排维护,避免非计划停机。同时,数据分析结果可直观展示于Web界面或移动APP,方便远程监控与管理决策。
结语
综上所述,实现工业机床CNC设备的远程监控数据上云是一个涉及多技术领域、跨平台协作的复杂工程。它不仅要求技术上的精确对接与创新,还需考虑数据的安全、合规及分析的有效性,最终目的是为了驱动智能制造的持续进步,提升整个产业链的智能化水平和竞争力。随着技术的不断成熟和应用案例的丰富,这一领域正展现出前所未有的活力与潜力。
相关文章:

工业机床CNC设备如何上云?
工业机床CNC设备如何上云? 工业机床的计算机数控(CNC)设备实现远程监控数据上云,是现代制造业智能化转型的关键一环。这一过程不仅能够实时监测设备状态、优化生产流程,还能通过大数据分析提升生产效率与产品质量&…...

Android C++系列:Linux进程间关系
1. 终端 在UNIX系统中,用户通过终端登录系统后得到一个Shell进程,这个终端成为Shell进 程的控制终端(Controlling Terminal),在前面文章我们说过,控制终端是保存在PCB中的信 息,而我们知道fork会复制PCB中的信息,因此由Shell进程启动的其它进程的控制终端也是 这个终端。…...

使用bypy丝滑传递百度网盘-服务器文件
前言 还在为百度网盘的数据集难以给服务器做同步而痛苦吗,bypy来拯救你了!bypy是一个强大而灵活的百度网盘命令行客户端工具。它是基于Python开发的开源项目,为用户提供了一种通过命令行界面与百度网盘进行交互的方式。使用bypy,…...

关于Python的类的一些理解
才发现python的类对象只能调用类方法 我想使用对类对象a使用系统调用的len方法就会报错 2.类对象a是什么? 答:是所有的带有self的成员变量 举例说明:红色的就是a里面的东西 class A:def __init__(self,data):self.datadataself.b1self.d{a…...

WEB安全基础:网络安全常用术语
一、攻击类别 漏洞:硬件、软件、协议,代码层次的缺陷。 后⻔:方便后续进行系统留下的隐蔽后⻔程序。 病毒:一种可以自我复制并传播,感染计算机和网络系统的恶意软件(Malware),它能损害数据、系统功能或拦…...

ubuntu防火墙指定端口开放设置
文章目录 打开某个端口查看防火墙状态和开放端口例子 在 Ubuntu 中管理防火墙通常使用 ufw(Uncomplicated Firewall)。以下是打开某个端口并查看防火墙状态的方法: 打开某个端口 启用 ufw(如果尚未启用): …...

Python OpenCV 教学取得视频资讯
这篇教学会介绍使用OpenCV,取得影像的长宽尺寸、以及读取影像中某些像素的颜色数值。 因为程式中的OpenCV 会需要使用镜头或GPU,所以请使用本机环境( 参考:使用Python 虚拟环境) 或使用Anaconda Jupyter 进行实作( 参考:使用Anaco…...

高频面试题基本总结回顾1(含笔试高频算法整理)
干货分享,感谢您的阅读! (暂存篇---后续会删除,完整版和持续更新见高频面试题基本总结回顾(含笔试高频算法整理)) 备注:引用请标注出处,同时存在的问题请在相关博客留言…...

【回溯+双指针算法题记录】回文字符串汇总
目录 验证回文串题目描述题目分析cpp代码 131. 分割回文串题目描述题目分析cpp代码 验证回文串 题目🔗 题目描述 如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 字…...

【AI资讯早报】AI科技前沿资讯概览:2024年7月10日早报
AI科技前沿资讯概览,涵盖了行业大会、技术创新、应用场景、行业动态等多个方面,全面展现了AI领域的最新发展动态和未来趋势。 一、人工智能大模型引领新业态 在2024年(第二十三届)中国互联网大会上,中国工程院院士邬贺…...

DDR3 SO-DIMM 内存条硬件总结(一)
最近在使用fpga读写DDR3,板子上的DDR3有两种形式与fpga相连,一种是直接用ddr3内存颗粒,另一种是通过内存条的形式与fpga相连。这里我们正好记录下和ddr3相关的知识,先从DDR3 SO-DIMM 内存条开始。 1.先看内存条的版本 从JEDEC下载…...
磁力搜索引擎是什么?为什么有些资源喜欢用磁力链接?
磁力链接是什么东西?在日常生活中,我们接触的比较多的下载链接是直链。 所谓的直链简单来说就是直接指向服务器文件资源的链接,如B站app的下载链接,这种链接有统一的服务器提供保障,通常比较稳定,可以追溯源…...

Vue基础--v-model/v-for/事件属性/侦听器
目录 一 v-model表单元素 1.1 v-model绑定文本域的value 1.1.1 lazy属性:光标离开再发请求 1.1.2 number属性:如果能转成number就会转成numer类型 1.1.3 trim属性:去文本域输入的前后空格 1.2v-model绑定单选checkbox 1.3代码展示 二 …...

『大模型笔记』GraphRAG:用于复杂数据发现的新工具现已在GitHub上发布
GraphRAG:用于复杂数据发现的新工具现已在GitHub上发布 文章目录 一. GraphRAG:用于复杂数据发现的新工具现已在GitHub上发布1. 评估和结果2. 研究见解和未来方向二. 参考文献一. GraphRAG:用于复杂数据发现的新工具现已在GitHub上发布 下载 GraphRAG今年早些时候,我们介绍…...

LabVIEW机器视觉技术在产品质量检测中有哪些应用实例
LabVIEW的机器视觉技术在产品质量检测中有广泛的应用,通过图像采集、处理和分析,实现对产品缺陷的自动检测、尺寸测量和定位校准,提高生产效率和产品质量。 1. 电子元器件质量检测 在电子制造业中,电子元器件的质量检测是确保产品…...

【Linux】多线程_2
文章目录 九、多线程2. 线程的控制 未完待续 九、多线程 2. 线程的控制 主线程退出 等同于 进程退出 等同于 所有线程都退出。为了避免主线程退出,但是新线程并没有执行完自己的任务的问题,主线程同样要跟进程一样等待新线程返回。 pthread_join 函数…...
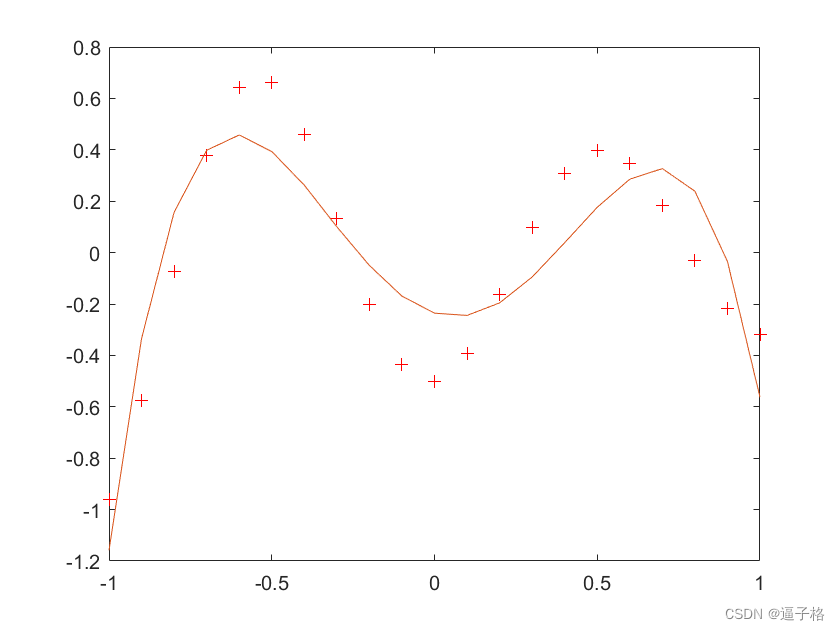
58、基于径向基神经网络的曲线拟合(matlab)
1、基于径向基神经网络的曲线拟合简介及原理 1)原理简介 基于径向基神经网络(Radial Basis Function Neural Network, RBFNN)的曲线拟合是一种常用的非线性拟合方法,通过在输入空间中使用径向基函数对数据进行处理,实…...
)
3.上传图片(阿里云空间,oss验证)
笔记 20240710 未验证,现在还没有阿里云空间,等买个sit环境就可以验证一下。 前端 页面 <!--页面--> <el-form-item label"优惠券图片" prop"couponImg"><single-upload v-model"dataForm.couponImg"&g…...

仪表板展示|DataEase看中国:2023年中国新能源汽车经济运行情况分析
背景介绍 随着政府机构、企业和个人对环保和可持续发展的高度关注,“新能源汽车”在全球范围内成为了一个热门话题。新能源汽车是指使用非传统燃料(如电能、氢能等)作为动力源的汽车。 在中国市场,新能源汽车产业蓬勃发展&#…...

“Numpy数据分析与挖掘:高效学习重点技能“
目录 # 开篇 # 补充 zeros & ones eye 1. numpy数组的创建 1.1 array 1.2 range 1.3 arange 1.4 常见的数据类型 1.5 astype 1.6 random.random() & round 2. numpy数组计算和数组计算 2.1 reshape 2.2 shape 2.3 将一维数组变成多维数组 2.4 指定一维…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

十二、【ESP32全栈开发指南: IDF开发环境下cJSON使用】
一、JSON简介 JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,具有以下核心特性: 完全独立于编程语言的文本格式易于人阅读和编写易于机器解析和生成基于ECMAScript标准子集 1.1 JSON语法规则 {"name"…...

Vue 3 Teleport 实战:优雅实现模态框、通知和全局组件
Vue 3 Teleport:突破 DOM 层级限制的组件渲染利器 在 Vue 应用开发中,组件通常与其模板的 DOM 结构紧密耦合。但当处理模态框(Modal)、通知(Toast)或全局 Loading 指示器时,这种耦合会成为障碍…...
