图论·Day01
P3371
P4779
P3371 【模板】单源最短路径(弱化版)
注意的点:
- 边有重复,选择最小边!
- 对于SPFA算法容易出现重大BUG,没有负权值的边时不要使用!!!
70分代码 朴素板dijsktra
- 爆空间
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
void solve() {cin >> n >> m >> s;vector<vector<int>>grid(n + 9, vector<int>(n + 9, INT_MAX));vector<int>dist(n + 9, INT_MAX);vector<bool>visited(n + 9, false);while (m--) {cin >> u >> v >> w;grid[u][v] = min(grid[u][v], w);}dist[s] = 0;for (int i = 1; i <= n; i++) {int cur = 1;int minDist = INT_MAX;for (int j = 1; j <= n; j++) {if (!visited[j] && dist[j] < minDist) {minDist = dist[j];cur = j;}}visited[cur] = true;for (int j = 1; j <= n; j++) {if (!visited[j] && grid[cur][j] != INT_MAX && dist[cur] + grid[cur][j] < dist[j]) {dist[j] = dist[cur] + grid[cur][j];}}/*cout << "select " << cur << endl;for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}cout << endl;*/}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
32分代码 SPFA
- 因为有重复指向的边,所有理论上边数可以无穷大,O(KM)的时间复杂度不确定性极大!
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {}
};
void solve() {cin >> n >> m >> s;vector<list<Edge>>grid(n + 9, list<Edge>());vector<int>dist(n + 9, INT_MAX); dist[s] = 0;queue<Edge>q;while (m--) {cin >> u >> v >> w;grid[u].push_back(Edge(v, w));}q.push({ s,0 });while (!q.empty()) {Edge cur = q.front();q.pop();for (auto item : grid[cur.v]) {if (item.w + dist[cur.v] < dist[item.v]) {dist[item.v] = dist[cur.v] + item.w;q.push(item);}}}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
AC代码 堆优化dijsktra
- 重复的边不影响
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, s, u, v, w;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {}
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;//从小排序}
};void solve() {cin >> n >> m >> s;vector<list<Edge>>grid(n + 9, list<Edge>());vector<int>dist(n + 9, INT_MAX); dist[s] = 0;vector<bool>visited(n + 9, false);priority_queue<Edge, vector<Edge>, cmp>q;while (m--) {cin >> u >> v >> w;grid[u].push_back(Edge(v, w));}q.push({ s,0 });while (!q.empty()) {Edge cur = q.top();q.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : grid[cur.v]) {if (!visited[item.v]&&item.w + dist[cur.v] < dist[item.v]) {dist[item.v] = item.w + dist[cur.v];q.push({ item.v,dist[item.v] });}}}for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
P1144
最短路计数
题目描述
给出一个 N N N 个顶点 M M M 条边的无向无权图,顶点编号为 1 ∼ N 1\sim N 1∼N。问从顶点 1 1 1 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 2 2 2 个正整数 N , M N,M N,M,为图的顶点数与边数。
接下来 M M M 行,每行 2 2 2 个正整数 x , y x,y x,y,表示有一条连接顶点 x x x 和顶点 y y y 的边,请注意可能有自环与重边。
输出格式
共 N N N 行,每行一个非负整数,第 i i i 行输出从顶点 1 1 1 到顶点 i i i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出 $ ans \bmod 100003$ 后的结果即可。如果无法到达顶点 i i i 则输出 0 0 0。
对于 100 % 100\% 100% 的数据, 1 ≤ N ≤ 1 0 6 1\le N\le10^6 1≤N≤106, 1 ≤ M ≤ 2 × 1 0 6 1\le M\le 2\times 10^6 1≤M≤2×106。
AC题解 堆优化dijsktra
- 多一段条件判断,不加入堆但是也起到了统计作用
else if (dist[cur.v] + item.w == dist[item.v]) {ct[item.v] += ct[cur.v];ct[item.v] %= 100003;}
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m, x, y;
struct Edge {int v, w;Edge(int a, int b) :v(a), w(b) {};
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;}
};
priority_queue<Edge,vector<Edge>,cmp>q;
void solve() {cin >> n >> m;vector<list<Edge>>grid(n+ 9, list<Edge>());vector<bool>visited(n+ 9, false);vector<int>dist(n+9, INT_MAX);vector<int>ct(n+9, 0);while (m--) {cin >> x >> y;grid[x].push_back(Edge(y, 1));grid[y].push_back(Edge(x, 1));}dist[1] = 0; ct[1] = 1;q.push({ 1,0 });while (!q.empty()) {Edge cur=q.top();q.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : grid[cur.v]) {if (dist[cur.v] + item.w < dist[item.v]) {dist[item.v] = dist[cur.v] + item.w;ct[item.v] = ct[cur.v];q.push({ item.v,dist[item.v] });}else if (dist[cur.v] + item.w == dist[item.v]) {ct[item.v] += ct[cur.v];ct[item.v] %= 100003;}}}//for (int i = 1; i <= n; i++) {// cout << dist[i] << " ";//}for (int i = 1; i <= n; i++) {cout << ct[i] << endl;}
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
P5905
【模板】全源最短路(Johnson)
题目描述
给定一个包含 n n n 个结点和 m m m 条带权边的有向图,求所有点对间的最短路径长度,一条路径的长度定义为这条路径上所有边的权值和。
注意:
-
边权可能为负,且图中可能存在重边和自环;
-
部分数据卡 n n n 轮 SPFA 算法。
输入格式
第 1 1 1 行: 2 2 2 个整数 n , m n,m n,m,表示给定有向图的结点数量和有向边数量。
接下来 m m m 行:每行 3 3 3 个整数 u , v , w u,v,w u,v,w,表示有一条权值为 w w w 的有向边从编号为 u u u 的结点连向编号为 v v v 的结点。
输出格式
若图中存在负环,输出仅一行 − 1 -1 −1。
若图中不存在负环:
输出 n n n 行:令 d i s i , j dis_{i,j} disi,j 为从 i i i 到 j j j 的最短路,在第 i i i 行输出 ∑ j = 1 n j × d i s i , j \sum\limits_{j=1}^n j\times dis_{i,j} j=1∑nj×disi,j,注意这个结果可能超过 int 存储范围。
如果不存在从 i i i 到 j j j 的路径,则 d i s i , j = 1 0 9 dis_{i,j}=10^9 disi,j=109;如果 i = j i=j i=j,则 d i s i , j = 0 dis_{i,j}=0 disi,j=0。
右图为样例 2 2 2 给出的有向图,红色标注的边构成了负环,注意给出的图不一定连通。
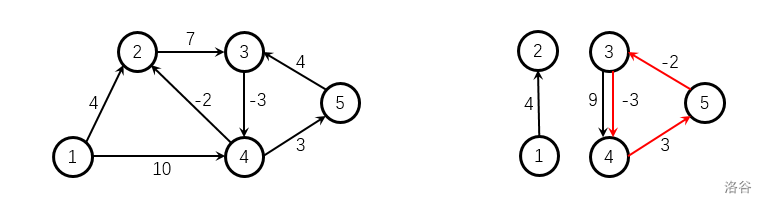
Johnson算法
- 数据溢出longlong的转换
h[item.v] = h[cur.v] + item.w;这段代码是Johnson算法的精髓,势能函数dist[j] + h[j] - h[st]由于路径上每一个边<i,j>都加入了h[i]-h[j],所以最短距离应该要 + 末位 - 首位,才是最终距离!
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n, m;
ll u,v,w;
void dijsktra(int st,vector<ll>dist);
struct Edge {ll v, w;Edge(ll a, ll b) :v(a), w(b) {};
};
class cmp {
public:bool operator()(const Edge& a, const Edge& b) {return a.w > b.w;}
};
ll inf = ll(1e9);
queue<Edge>q;
vector<int>ct(3009, 0);
vector<list<Edge>>edges(3009, list<Edge>());
vector<ll>h(3009, inf);vector<ll>dist(3009, inf);
priority_queue<Edge, vector<Edge>, cmp>s;
bool visited[3009];
void solve() {cin >> n >> m;while(m--) {cin >> u >> v >> w;edges[u].push_back({ v,w });}for (int i = 1; i <= n; i++) {edges[0].push_back({ i,0 });}h[0] = 0;q.push({ 0,0 }); ct[0] = 1;while (!q.empty()) {Edge cur = q.front();q.pop();if (ct[cur.v] >= n) {cout << -1;return;}for (auto item : edges[cur.v]) {if (h[cur.v] + item.w < h[item.v]) {h[item.v] = h[cur.v] + item.w;ct[item.v] ++;q.push(item); }}}/* cout << "h" << endl;for (int i = 0; i <= n; i++) {cout << h[i]<<" ";}cout << endl;*//*重组edges数组*/for (int i = 1; i <= n; i++) {for (auto& item : edges[i]) {item.w = item.w+h[i] - h[item.v];}}for (int i = 1; i <= n; i++) {dijsktra(i,dist);}
}
void dijsktra(int st,vector<ll>dist) {memset(visited, false, sizeof(visited));dist[st] = 0; s.push({ st,0 });while (!s.empty()) {Edge cur = s.top();s.pop();if (visited[cur.v]) {continue;}visited[cur.v] = true;for (auto item : edges[cur.v]) {if (!visited[item.v]&&dist[cur.v] + item.w < dist[item.v]) {dist[item.v] = item.w+ dist[cur.v];s.push({ item.v,dist[item.v] });}}}/*for (int i = 1; i <= n; i++) {cout << dist[i] << " ";}cout << endl;*/ll ans = 0;for (int j = 1; j <= n; j++) {if (dist[j] == inf) {ans += ll(j) * dist[j];}else {ans += ll(j) * (dist[j] + h[j] - h[st]);}}cout << ans << endl;
}
int main() {std::ios::sync_with_stdio(false);std::cin.tie(0); std::cout.tie(0);solve();return 0;
}
今日总结
- dijsktra不能用于负权值
- Bellman可以用于检测负权回路
- SFPA算法不要轻易用!容易爆死!
- Floyd 算法时间复杂度O(n3),dijsktra O(mlogm),Johnson算法时间复杂度接近 O(nmlogn),相当于用SFPA扫除了dijsktra不能求负权值边的障碍,最终还是要归结于dijsktra算法堆优化版来!说人话就是Bellman和SFPA太慢,dijsktra用不了,所以采用Johnson算法!
相关文章:

图论·Day01
P3371 P4779 P3371 【模板】单源最短路径(弱化版) 注意的点: 边有重复,选择最小边!对于SPFA算法容易出现重大BUG,没有负权值的边时不要使用!!! 70分代码 朴素板dijsk…...

hutool ExcelUtil 导出导入excel
引入依赖 <dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.15</version></dependency>文件导入 public void savelist(String filepath,String keyname){ExcelReader reader Exce…...

打卡第7天-----哈希表
继续坚持✊,我现在看到leetcode上的题不再没有思路了,真的是思路决定出路,在做题之前一定要把思路梳理清楚。 一、四数相加 leetcode题目编号:第454题.四数相加II 题目描述: 给定四个包含整数的数组列表 A , B , C , …...
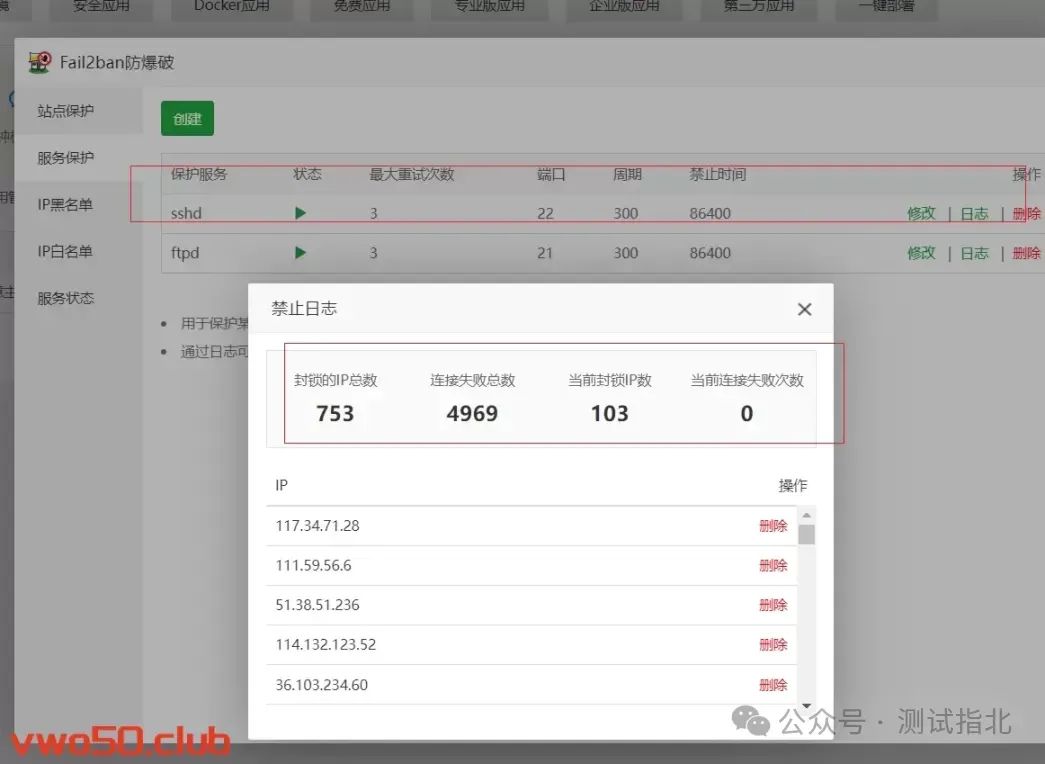
【Linux】WEB网站网络防火墙(WAF软件)Fail2ban:保护服务器免受恶意攻击的必备工具
随着互联网的迅速发展,服务器的安全性日益成为用户和管理员关注的焦点。恶意攻击者不断寻找机会侵入服务器,窃取敏感信息、破坏数据或者滥用系统资源。为了抵御这些威胁,许多安全工具应运而生,其中一款备受推崇的工具就是 Fail2ba…...

妙笔生词智能写歌词软件:创新助力还是艺术之殇?
在音乐创作日益普及和多样化的当下,各种辅助工具层出不穷,妙笔生词智能写歌词软件便是其中之一。那么,它到底表现如何呢? 妙笔生词智能写歌词软件(veve522)的突出优点在于其便捷性和高效性。对于那些灵感稍…...

力扣hot100-普通数组
文章目录 题目:最大子数组和方法1 动态规划方法2 题目:合并区间题解 题目:轮转数组方法1-使用额外的数组方法2-三次反转数组 题目:除自身以外数组的乘积方法1-用到了除法方法2-前后缀乘积法 题目:最大子数组和 原题链…...

深入浅出Transformer:大语言模型的核心技术
引言 随着自然语言处理(NLP)领域的不断发展,Transformer模型逐渐成为现代大语言模型的核心技术。无论是BERT、GPT系列,还是最近的T5和Transformer-XL,这些模型的背后都离不开Transformer架构。本文将详细介绍Transfor…...

MacOS隐藏文件打开指南
MacOS隐藏文件打开指南 方法一: 直接按下键盘上的【commandshift.】,这时候就可以在mac系统中就会自动显示隐藏的文件夹了 方法二: 在终端查看 ls -la...

grafana数据展示
目录 一、安装步骤 二、如何添加喜欢的界面 三、自动添加注册客户端主机 一、安装步骤 启动成功后 可以查看端口3000是否启动 如果启动了就在浏览器输入IP地址:3000 账号密码默认是admin 然后点击 log in 第一次会让你修改密码 根据自定义密码然后就能登录到界面…...

53-4 内网代理6 - frp搭建三层代理
前提:53-3 内网代理5 - frp搭建二级代理-CSDN博客 三级网络代理 在办公区入侵后,发现需要进一步渗透核心区网络(192.168.60.0/24),并登录域控制器的远程桌面。使用FRP在EDMZ区、办公区与核心区之间建立三级网络的SOCKS5代理,以便访问核心区的域控制器。 VPS上的FRP服…...

SQLite 命令行客户端 + HTA 实现简易UI
SQLite 命令行客户端 HTA 实现简易UI SQLite 客户端.hta目录结构参考资料 仅用于探索可行性,就只实现了 SELECT。 SQLite 客户端.hta <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html; cha…...

TikTok小店推出“百万英镑俱乐部”,实力宠卖家!
TikTok Shop近期在英国市场重磅推出了“百万英镑俱乐部”激励计划,这一举措旨在通过一系列诱人福利,助力商家在TikTok平台上实现销售飞跃。该计划不仅彰显了TikTok Shop对于商家成长的深切关怀,更以实际行动诠释了“实力宠卖家”的承诺。 我…...

路径规划 | 基于蚁群算法的三维无人机航迹规划(Matlab)
目录 效果一览基本介绍程序设计参考文献 效果一览 基本介绍 基于蚁群算法的三维无人机航迹规划(Matlab)。 蚁群算法(Ant Colony Optimization,ACO)是一种模拟蚂蚁觅食行为的启发式算法。该算法通过模拟蚂蚁在寻找食物时…...
.Net C#执行JavaScript脚本
文章目录 前言一、安装二、执行 JavaScript 脚本三、与脚本交互四、JS 调用 C# 方法五、多线程使用总结 前言 ClearScript 是一个 .NET 平台下的开源库,用于在 C# 和其他 .NET 语言中执行脚本代码。它提供了一种方便和安全的方法来将脚本与应用程序集成,…...

企业应对策略:全面防御.DevicData-P-xxxxxx勒索病毒
引言 在数字化时代,网络安全已成为不可忽视的重要议题。随着互联网的普及,各种网络威胁层出不穷,其中勒索病毒以其独特的攻击方式和巨大的破坏性,给个人用户和企业带来了严重的经济损失和数据安全风险。在众多勒索病毒中ÿ…...

记一次mysql导出到达梦数据库
DM8管理工具 DM管理工具(官方)DBeaver - jdbc驱动 MySql迁移到DM8 使用官方DM数据迁移工具 新建迁移工程选择MySQL>DM填写mysql连接信息、添加dm连接信息执行 DM8数据脚本制作过程 使用DM管理工具 导出全部:进入对应模式>表>选…...

2024年高压电工证考试题库及高压电工试题解析
题库来源:安全生产模拟考试一点通公众号小程序 2024年高压电工证考试题库及高压电工试题解析是安全生产模拟考试一点通结合(安监局)特种作业人员操作证考试大纲和(质检局)特种设备作业人员上岗证考试大纲随机出的高压…...

完美解决ImportError: cannot import name ‘idnadata‘的正确解决方法,亲测有效!!!
完美解决ImportError: cannot import name idnadata’的正确解决方法,亲测有效!!! 亲测有效 完美解决ImportError: cannot import name idnadata的正确解决方法,亲测有效!!!报错问题…...

完美解决windows开机时,系统提示此windows副本不是正版的正确解决方法,亲测有效!!!
完美解决windows开机时,系统提示此windows副本不是正版的正确解决方法,亲测有效!!! 亲测有效 完美解决windows开机时,系统提示此windows副本不是正版的正确解决方法,亲测有效!&#…...

树莓派采集系统
树莓派(Raspberry Pi)是一款非常受欢迎的小型单板计算机,因其低成本、低功耗以及丰富的I/O接口,非常适合用来搭建数据采集系统。无论是环境监测、智能家居、工业自动化,还是科学实验,树莓派都能胜任。以下是…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
