数据结构--二叉树相关习题5(判断二叉树是否是完全二叉树 )
1.判断二叉树是否是完全二叉树
辨别:
不能使用递归或者算节点个数和高度来判断。

满二叉树可以用高度和节点来判断,因为是完整的。
但是完全二叉树前面是满的,但是最后一层是从左到右连续这种
如果仍然用这种方法的话,如下图两个识别方法是一样的,但是无法准确识别

完全二叉树:前h-1层是满的,最后一层是从左到右连续。
如果走层序那么一定是连续的,也就是说要通过层序遍历来走。
思路:1.层序遍历走,空也进序列。
2.遇到第一个空时开始判断,如果后面都为空则是完全二叉树,若空后面还出席那非空的情况则说明不是完全二叉树。
 代码实现:
代码实现:
//判断二叉树是否是完全二叉树
bool TreeComplete(BTNode* root)
{ Queue q;//仍然使用队列去实现QueueInit(&q);if (root)QueuePush(&q,root)while (!QueueEmpty){BTNode* front = QueueFront(&q);QueuePop(&q);//遇到第一个空就可以开始判断,如果队列中还有非空,就不是完全二叉树。if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}while (!QueueEmpty){BTNode* front = QueueFront(&q);QueuePop(&q);//如果仍有非空元素,直接
// return false;if (front){QueueDestroy(&q);//如果存在非空。return false;}QueueDestroy(&q);return true;
//最终QueueDestroy,再返回}
}补充队列的一系列实现
void QueueInit(Queue* pq)
{assert(pq);pq->phead = NULL;pq->ptail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}// 队尾插入
void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return;}newnode->next = NULL;newnode->val = x;if (pq->ptail == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}// 队头删除
void QueuePop(Queue* pq)
{assert(pq);assert(pq->size != 0);/*QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;if (pq->phead == NULL)pq->ptail = NULL;*/// 一个节点if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else // 多个节点{QNode* next = pq->phead->next;free(pq->phead);pq->phead = next;}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->phead);return pq->phead->val;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->ptail);return pq->ptail->val;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}
//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}相关文章:

数据结构--二叉树相关习题5(判断二叉树是否是完全二叉树 )
1.判断二叉树是否是完全二叉树 辨别: 不能使用递归或者算节点个数和高度来判断。 满二叉树可以用高度和节点来判断,因为是完整的。 但是完全二叉树前面是满的,但是最后一层是从左到右连续这种 如果仍然用这种方法的话,如下图…...

Python 轻松生成多种条形码、二维码 (Code 128、EAN-13、QR code等)
条形码和二维码是现代信息交换和数据存储的重要工具,它们将信息以图形的形式编码,便于机器识别和数据处理,被广泛应用于物流、零售、医疗、教育等各领域。 本文将介绍如何使用Python快速生成各种常见的条形码如Code 128、EAN-13,…...

Python: 分块读取文本文件
在处理大文件时,逐行或分块读取文件是很常见的需求。下面是几种常见的方法,用于在 Python 中分块读取文本文件: 1、问题背景 如何分块读取一个较大的文本文件,并提取出特定的信息? 问题描述: fopen(blank.txt,r) quot…...

服务攻防——中间件Jboss
文章目录 一、Jboss简介二、Jboss渗透2.1 JBoss 5.x/6.x 反序列化漏洞(CVE-2017-12149)2.2 JBoss JMXInvokerServlet 反序列化漏洞(CVE-2015-7501)2.3 JBossMQ JMS 反序列化漏洞(CVE-2017-7504)2.4 Adminis…...

宏碁F5-572G-59K3笔记本笔记本电脑拆机清灰教程(详解)
1. 前言 我的笔记本开机比较慢,没有固态,听说最近固态比较便宜,就想入手一个,于是拆笔记本看一下有没有可以安的装位置。(友情提示,在拆机之前记得洗手并擦干,以防静电损坏电源器件)…...

基于FPGA的LDPC编译码算法设计基础知识
基于FPGA的LDPC编译码算法设计基础知识 数字电路(数电)知识模拟电路(模电)知识1. 放大器1.1. 晶体管放大器1.2. 运算放大器1.3. 管子放大器(真空管放大器)微处理器/单片机知识其他相关知识 基于FPGA的算法设…...

国际网课平台Udemy上的亚马逊云科技AWS免费高分课程和创建、维护EC2动手实践
亚马逊云科技(AWS)是全球云行业最🔥火的云平台,在全球经济形势不好的大背景下,通过网课学习亚马逊云科技AWS基础备考亚马逊云科技AWS证书,对于找工作或者无背景转行做AWS帮助巨大。欢迎大家关注小李哥,及时了解世界最前…...

空中交通新动能!2024深圳eVTOL展动力电池展区核心内容抢先看!
空中交通新动能!2024深圳eVTOL展动力电池展区核心内容抢先看! 关键词:2024深圳eVTOL展 动力电池 高能量密度电池 高性能电池材料 作为2024深圳eVTOL展重要组成部分,2024深圳eVTOL动力电池展将于9月23-25日在深圳坪山燕子湖国际会…...

代码江湖:Python 中的进程与线程
大家好,我是阔升。今天,咱们来聊聊 Python 中的两个"老熟人"——进程和线程。这两个概念可以说是 Python 多任务编程中的"双子星",既相似又不同,让不少小伙伴们头疼不已。不过别担心,今天我们就来…...
上求解生成矩阵G)
根据H在有限域GF(2^m)上求解生成矩阵G
原理 有时间再补充。 注1:使用高斯消去法。如果Py不为单位阵,则说明进行了列置换,此时G不是系统形式。 注2:校验矩阵H必须是行满秩才存在对应的生成矩阵G,且生成矩阵G通常不唯一。 matlab实现:只做列置…...

Django 实现子模版继承父模板
背景 Django的占位符,如果不继承父模板的内容,会被子模版所覆盖,有些业务场景子模版也需要使用到父模板中的内容 可以使用Django自带的标签{% block super %}来实现此效果 base.html 最基础html,相当于第一层html,bl…...

数据安全治理:从库级权限申请到表级权限申请
背景 随着数据安全意识的提高,企业越来越重视数据治理和权限管理。传统数仓大多对库级别进行读写授权,仅对人工标记的敏感库进行表级别授权,但由于敏感等级是由人为标记,错误率较高,故期望将权限申请流程细化到表级申…...

vue3源码(六)渲染原理-runtime-core
1.依赖关系 runtime-dom 依赖于runtime-core,runtime-core 依赖于reactivity和sharedruntime-core提供跨平台的渲染方法createRenderer,用户可以自己传递节点渲染的渲染方法renderOptions,本身不关心用户使用什么APIruntime-dom提供了为浏览器而生的渲染…...

python拆分Excel数据,自动发邮箱
import pandas as pd import poplib import email from email.header import decode_header from email.parser import Parser df = pd.read_excel("年假明细表.xlsx") depts = df["部门"].unique() for dept in depts: department_df = df[df[&q…...
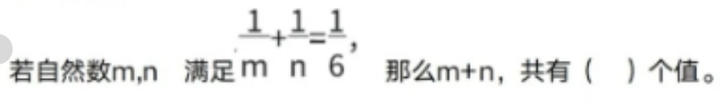
2024年福州延安中学夏季拿云杯拔尖创新人才素养测试(小高组)
1、选择题 那么,mn的值是( ) A、1243 B、1343 C、4029 D、4049 2、填空题 一副扑克牌共54张,其中1到13点各有 4张,每个数字黑色红色各两张,还有两张王牌,至少要取出( )…...
)
ES6 之 Promise 构造函数知识点总结 (四)
Promise 是异步编程的一种解决方案,比传统的解决方案——回调函数和事件——更合理和更强大。它由社区最早提出和实现,ES6 将其写进了语言标准,统一了用法,原生提供了 Promise 对象。 Promise 对象有以下两个特点。 对象的状态不受…...

KIVY 3D Rotating Monkey Head¶
7 Python Kivy Projects (With Full Tutorials) – Pythonista Planet KIVY 3D Rotating Monkey Head kivy 3D 旋转猴子头How to display rotating monkey example in a given layout. Issue #6688 kivy/kivy GitHub 3d 模型下载链接 P99 - Download Free 3D model by …...

测试几个 ocr 对日语的识别情况
测试几个 ocr 对日语的识别情况 1. EasyOCR2. PaddleOCR3. Deepdoc(识别pdf中图片)4. Deepdoc(识别pdf中文字)5. Nvidia neva-22b6. Claude 3.5 sonnet 识别图片中的文字7. Claude 3.5 sonnet 识别 pdf 中表格8. OpenAI gpt-4o 识…...

华为机考前准备工作
很多同学在刷完真题后,就直接去考试了,会发现不是卡在了题目的难度上,而是卡在了代码数据的如何输入上。为了避免各位有志之士忽略小细节而导致的前功尽弃,博主特意总结了华为机考试题数据输入的几种情况及其源代码,仅…...

偏差、方差(训练误差,验证误差)
目录 一、偏差、方差:二、正则化参数λ对偏差、方差的影响:三、训练集规模对偏差、方差的影响:四、模型复杂度对偏差、方差的影响:五、方差、偏差如何帮助训练:1.高偏差解决方法:2.高方差解决方法ÿ…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
