[数据结构] 归并排序快速排序 及非递归实现
()标题:[数据结构] 归并排序&&快速排序 及非递归实现
@水墨不写bug

(图片来源于网络)
目录
(一)快速排序
类比递归谋划非递归
快速排序的非递归实现:
(二)归并排序
归并排序的递归实现:
归并排序的非递归
细节处理:
归并排序的非递归实现:
正文开始:
(一)快速排序
快速排序一般通过递归来实现,但是递归也有递归的劣势:当递归程度太深,会导致栈溢出的问题,我们在前面的分享中已经讲解了快速排序的递归实现,这里不再赘述,为了便于讲解,直接给出快速排序的递归实现:
int GetRandomKey(vector<int>& nums, int l, int r) {return nums[rand() % (r - l + 1) + l]; } void QuickSort(vector<int>& nums,int l,int r) {//递归出口if (l >= r)return;int key = GetRandomKey(nums,l,r);int left = l - 1, right = r + 1, cur = l;while (cur < right){if (nums[cur] < key)swap(nums[cur++], nums[++left]);else if (nums[cur] == key)cur++;elseswap(nums[--right],nums[cur]);}QuickSort(nums, l, left);QuickSort(nums, right, r); }这里给出的快速排序的递归实现是比较完备的优化过的快排,它解决了:
(1)、key选取不合适导致的分区不平衡的问题。
(2)、key在数据中重复大量出现的问题。
递归的过程:
其实通过观察快排的过程,我们会发现之所以在传入参数的时候必须传入左右区间,是因为我们在快排的内部过程中并不确定需要对哪一个区间的数据 进行排序。
随着递归的进行,函数栈帧逐层开辟,每一层函数栈帧中都存有需要排序的区间的边界值。
每一个函数栈帧都有一个
左区间端点值 :l
右区间端点值 :r
递归是在栈区进行的,我们既然需要避免计算机自己的栈区溢出,那么我们为什么不自己模拟一个栈呢?
递归原理:
通过模拟一个栈,来协助存储左右区间端点值,以此来达到让快排正常进行的目的。
因此,重要的是需要对自己实现的栈精确的控制。
类比递归谋划非递归
什么时候递归停止?
当所有递归都返回的时候递归停止——当模拟实现的栈为空的时候停止迭代;
递归出口的条件设置?
当递归区间不存在的时候,递归通过return返回到上一层——当递归区间不存在的时候,直接进入下一次迭代,这里就用到了continue;
如何准确的控制接收的左右区间的端点值?
通过栈来模拟,需要注意栈的后进先出的特点,push的顺序和pop的顺序是相反的,比如:先push左端点,再push右端点;在top的时候,先取得的是右端点值,pop后,top再取得的是左端点值。
快速排序的非递归实现:
void QuickSort_NoR(vector<int>& nums,int l1,int r1) {stack<int> st;st.push(l1);st.push(r1);while (!st.empty()){int r = st.top();st.pop();int l = st.top();st.pop();if (l >= r)continue;int left = l - 1, right = r + 1, cur = l;int key = GetRandomKey(nums, l, r);while (cur < right){if (nums[cur] < key)swap(nums[cur++], nums[++left]);else if (nums[cur] == key)cur++;elseswap(nums[--right], nums[cur]);}st.push(right);st.push(r);st.push(l);st.push(left);} }
(二)归并排序
归并是一种算法,当归并应用在排序中,实际上的操作就是将两个有序数组合并为一个有序数组的过程。
归并排序一般通过非递归实现,其核心思想是分治,但是递归的缺点明显,本文上半部分也说明了递归的缺点,因此非递归实现归并有很大意义。
时间复杂度:O(N*logN)
空间复杂度:O(N)
稳定性:稳定归并的缺点:需要O(N)的空间复杂度
我们在实现归并排序的时候,需要注意的是:
(1)、需要一个N个空间的数组辅助进行排序,由于递归次数很多,在递归过程中创建数组代价太大,所以我们在全局来创建一个数组tem,作为辅助,不仅在每一层递归中都可使用,也节省了资源。
(2)、归并的主要过程通过三目运算符处的逻辑实现。
(3)、三目运算符之后,需要再将没有遍历到末尾的数据继续添加到tem末尾即可,此时归并结束。
(4)、最终不要忘了将tem内的数据拷贝回原数组。
归并排序的递归实现:
vector<int> tem(0); void MergeSort(vector<int>& nums,int l,int r) {if (l >= r)return;int mid = (r - l) / 2 + l;int cur1 = l, cur2 = mid + 1;MergeSort(nums, l, mid);MergeSort(nums, mid + 1, r);int i = 0;while (cur1 <= mid && cur2 <= r){tem[i++] = nums[cur1] < nums[cur2] ?nums[cur1++] : nums[cur2++];}while (cur1 <= mid)tem[i++] = nums[cur1++];while (cur2 <= r)tem[i++] = nums[cur2++];for (int j = l; j <= r;++j){nums[j] = tem[j - l];} } int main() {vector<int> nums = { 99,0,7,5,44,3,78,653,90,81 };tem.resize(nums.size());Print(nums);MergeSort(nums,0,nums.size()-1);Print(nums);return 0; }
归并排序的非递归
想要实现归并的非递归,在整体上需要换一种思路。
在局部上,归并的逻辑仍然是与递归是一致的;
我们在思考的时候要将问题逐渐拆成一个一个的小问题:
(1)、归并过程:
将[begin1,end1],[begin2,end2]归并为一个有序的数组,算法本质和步骤和非递归的实现方法完全一致;
(2)、非递归省去了进入递归的过程,而是直接将数组分为多份,每一份有gap个:
gap开始取1,表示一个数字就是一个区间,这个步骤是数组本身就满足的;
gap每次*2,表示区间扩大的过程,这样一来gap逐渐扩大,就在思路上完成了归并;
通过分析,你也知道了最重要的是对区间的左右端点的控制,也就是需要控制好区间的偏移和越界问题。
细节处理:
(1)区间的偏移:
通过一个循环,循环变量为k,两个区间的开始位置是由k来决定的,用k来控制区间的偏移:由于每次是归并两个数组,所以每次归并完成后,k+=2*gap:
演示(以gap=2为例):
偏移后:(k+=2*gap)
(2)区间的越界:
我们上图举的例子是一个特殊情况,数组元素个数刚好够归并需要的元素,如果元素有9个而不是8个,这就需要考虑区间的越界问题了。
当数组的长度更加一般时,会出现区间的越界问题,对于每一个区间端点:
begin1:由k决定(k< n,所以不可能越界)
end1:begin1+gap-1,有可能越界;如果越界,数组个数只有一个,则不再归并。
begin2:begin1+gap,可能越界;如果越界,数组个数只有一个,则不再归并。
end2:begin1+2*gap-1;可能越界;如果越界,数组个数有两个,修正end2的位置后再归并。
归并排序的非递归实现:
void MergeSort_NoR(vector<int>& nums, int l, int r) {int n = nums.size();int gap = 1;while (gap < n){for (int k = 0; k < n; k += 2*gap){// 对两组进行归并 [beign1,end1] [begin2,end2] // 组内宽度gap int begin1 = k, end1 = begin1 + gap - 1;int begin2 = end1 + 1, end2 = begin2 + gap - 1;if (end1 >= n || begin2 >= n)break;if (end2 >= n)end2 = n-1;int i = k;while (begin1 <= end1 && begin2 <= end2)tem[i++] = nums[begin1] < nums[begin2] ?nums[begin1++] : nums[begin2++];while (begin1 <= end1) tem[i++] = nums[begin1++];while (begin2 <= end2) tem[i++] = nums[begin2++];for (int j = k; j <= end2; ++j)nums[j] = tem[j];}gap *= 2;} }
完~
未经作者同意禁止转载
相关文章:

[数据结构] 归并排序快速排序 及非递归实现
()标题:[数据结构] 归并排序&&快速排序 及非递归实现 水墨不写bug (图片来源于网络) 目录 (一)快速排序 类比递归谋划非递归 快速排序的非递归实现: (二)归并排序 归…...

面试题 12. 矩阵中的路径
矩阵中的路径 题目描述示例 题解 题目描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成࿰…...

钉钉扫码登录第三方
钉钉文档 实现登录第三方网站 - 钉钉开放平台 (dingtalk.com) html页面 将html放在 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>登录</title>// jquery<script src"http://code.jqu…...

多GPU系统中的CUDA设备不可用问题
我们在使用多GPU系统时遇到了CUDA设备不可用的问题,详细情况如下: 问题描述: 我们在一台配备有8块NVIDIA GeForce RTX 3090显卡的服务器上运行CUDA程序时,遇到了如下错误: cudaErrorDevicesUnavailable: CUDA-capabl…...

python的列表推导式
文章目录 前言一、解释列表推导式二、在这句代码中的应用三、示例四、使用 for 循环的等价代码总结 前言 看看这一行代码:questions [q.strip() for q in examples["question"]] ,问题是最外层的 中括号是做什么的? 最外层的中括…...

类与对象(2)
我们在了解了类的简单创建后,需要对类的创建与销毁有进一步的了解,也就是对于类的构造函数与析构函数的了解。 目录 注意: 构造函数的特性: 析构函数: 注意: 该部分内容为重难点内容,在正常…...

迂回战术:“另类“全新安装 macOS 15 Sequoia beta2 的极简方法
概述 随着 WWDC 24 的胜利闭幕,Apple 平台上各种 beta 版的系统也都“跃跃欲出”,在 mac 上自然也不例外。 本次全新的 macOS 15 Sequoia(红杉)包含了诸多重磅升级,作为秃头开发者的我们怎么能不先睹为快呢࿱…...
)
如何设计一个秒杀系统,(高并发高可用分布式集群)
设计一个高并发、高可用的分布式秒杀系统是一个非常具有挑战性的任务,需要从架构、数据库、缓存、并发控制、降级限流等多个维度进行考虑。以下是一个典型的秒杀系统设计思路: 1. 系统架构 微服务架构 拆分服务:将系统功能拆分为多个微服务…...
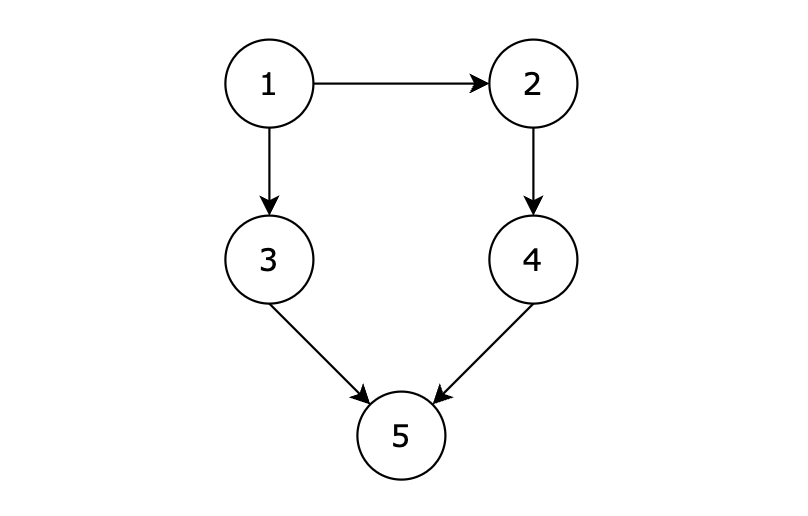
深度优先搜索(所有可达路径)
参考题目:所有可达路径 题目描述 给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。 输入描述 第一行包含两个整数 N,M&…...
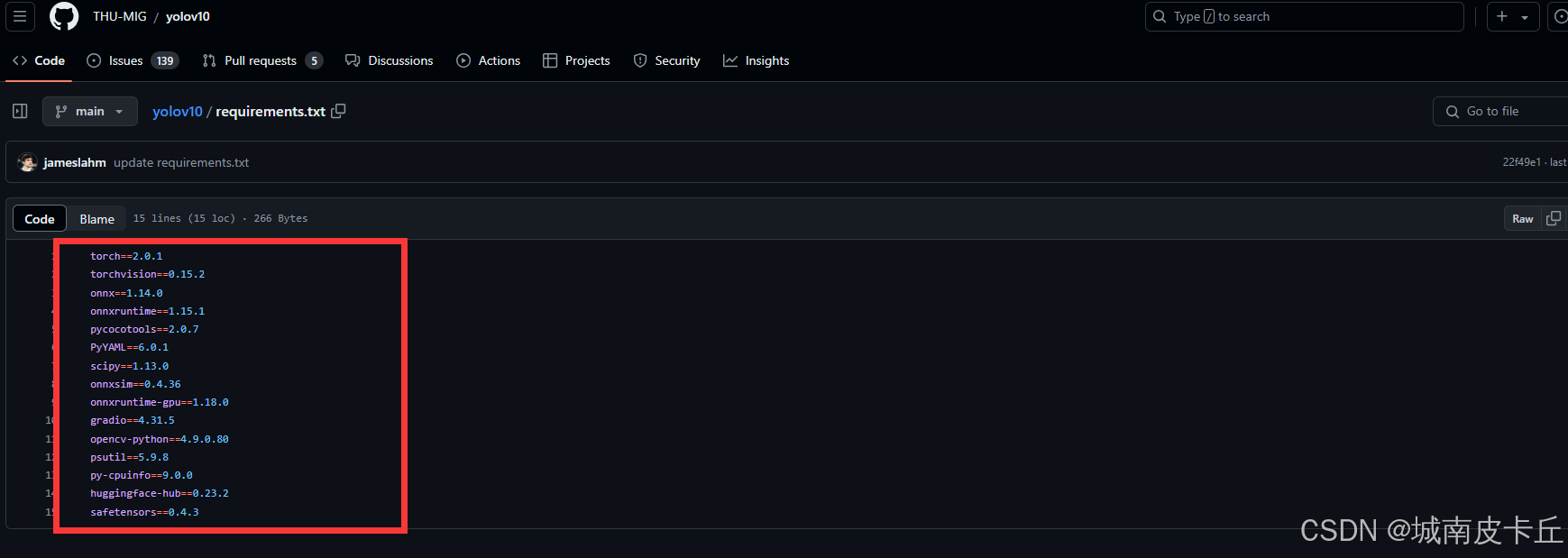
如何配置yolov10环境?
本文介绍如何快速搭建起yolov10环境,用于后续项目推理、模型训练。教程适用win、linux系统 yolo10是基于yolo8(ultralytics)的改进,环境配置跟yolo8几乎一模一样。 目录 第1章节:创建虚拟环境 第2章节:…...

『大模型笔记』GraphRAG:利用复杂信息进行发现的新方法!
GraphRAG:利用复杂信息进行发现的新方法! 文章目录 一. GraphRAG:利用复杂信息进行发现的新方法!1. 将RAG应用于私人数据集2. 整个数据集的推理3. 创建LLM生成的知识图谱4. 结果指标5. 下一步二. 参考文献微软官方推文:https://www.microsoft.com/en-us/research/blog/gra…...

数据结构1:C++实现变长数组
数组作为线性表的一种,具有内存连续这一特点,可以通过下标访问元素,并且下标访问的时间复杂的是O(1),在数组的末尾插入和删除元素的时间复杂度同样是O(1),我们使用C实现一个简单的边长数组。 数据结构定义 class Arr…...

C++入门基础篇(下)
目录 6.引用 6.1 引用的特性 6.2 const引用 7.指针和引用的关系 8.内联函数 9.nullptr 6.引用 引⽤不是新定义⼀个变量,⽽是给已存在变量取了⼀个别名,编译器不会为引⽤变量开辟内存空间, 它和它引⽤的变量共⽤同⼀块内存空间。比如&a…...
LabVIEW图像分段线性映射
介绍了如何使用LabVIEW对图像进行分段线性映射处理,通过对特定灰度值区间进行不同的线性映射调整,以优化图像的显示效果。案例中详细展示了如何配置和使用LabVIEW中的图像处理工具,包括设置分段区间、计算映射参数和应用映射函数等步骤。 实…...

Linux开发:进程件通过UDS传递内存文件句柄
Linux开发:进程间通过Unix Domain Socket传递文件描述符-CSDN博客 介绍了通过UDS传递文件描述符 Linux开发:通过memfd_create创建一个内存文件-CSDN博客 介绍了如果创建一个内存文件 将两者相结合,就可以通过UDS传递一块内存文件句柄也就是内存数据 //uds_fd.hpp #pragma …...

Internet Download Manager6.42最新下载器互联网冲浪小能手们!
今天我要来种草一个超级棒的宝贝——Internet Download Manager(简称 IDM)。这个小家伙简直是下载界的“速度与激情”代言人,让我彻底告别了等待的日子。🎉 IDM马丁正版下载如下: https://wm.makeding.com/iclk/?zoneid34275 …...

Vue 使用Audio或AudioContext播放本地音频
使用Audio 第一种 使用标签方式 <audio src"./tests.mp3" ref"audio"></audio><el-button click"audioPlay()">播放Audio</el-button>audioPlay() {this.$refs.audio.currentTime 0;this.$refs.audio.play();// this.$…...

从数据仓库到数据湖(上):数据湖导论
文章目录 一、什么是数据湖?起源数据湖的特征 二、为什么要用数据湖?三、数据湖与数据仓库的区别数据仓库和数据湖的对比 四、数据湖本质数据存储架构数据处理工具:三类第一类工具第二类工具第三类工具 小结 五、总结六、参考资料 一、什么是…...
:深入探索 Perl 中的数组与列表操作)
Perl 语言开发(六):深入探索 Perl 中的数组与列表操作
目录 1. 数组和列表的基本概念 1.1 数组的定义与特点 1.2 列表的定义与特点 2. 数组的基本操作 2.1 访问数组元素 2.2 数组的长度 2.3 添加和删除元素 2.4 切片操作 2.5 迭代数组 3. 列表的常见操作 3.1 创建和使用列表 3.2 列表的上下文 3.3 列表和数组的转换 3…...

统一视频接入平台LntonCVS视频监控平台具体功能介绍
LntonCVS视频监控平台是一款基于H5技术开发的安防视频监控解决方案,专为全球范围内不同品牌、协议及设备类型的监控产品设计。该平台提供了统一接入管理,支持标准的H5播放接口,使其他应用平台能够快速集成视频功能。无论开发环境、操作系统或…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...



