华为OD机试(C卷,200分)- 字符串拼接、田忌赛马
(C卷,200分)- 字符串拼接
题目描述
给定 M(0 < M ≤ 30)个字符(a-z),从中取出任意字符(每个字符只能用一次)拼接成长度为 N(0 < N ≤ 5)的字符串,
要求相同的字符不能相邻,计算出给定的字符列表能拼接出多少种满足条件的字符串,
输入非法或者无法拼接出满足条件的字符串则返回0。
输入描述
给定的字符列表和结果字符串长度,中间使用空格(" ")拼接
输出描述
满足条件的字符串个数
用例
输入 abc 1
输出 3
说明 给定的字符为a,b,c,结果字符串长度为1,可以拼接成a,b,c,共3种
输入 dde 2
输出 2
说明 给定的字符为dde,结果字符串长度为2,可以拼接成de,ed,共2种
题目解析
这道题目和46.全排列的区别在与给定一个可包含重复字母的序列,要返回所有不重复的全排列。
还要强调的是去重一定要对元素进行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
去重关键代码
if(i>0&&str[i]==str[i-1])continue;
#include <stdio.h>
#include <stdlib.h>
int pathTop=0;
int ansTop=0;
int len=0;
char str[100];
void backtracking(int level,int size,int* used){if(pathTop==size){ansTop++;return;}for(int i=0;i<len;i++){if(i>0&&str[i]==str[i-1])continue;if(used[i])continue;used[i]=1;pathTop++;backtracking(level+1,size,used);used[i]=0;pathTop--;}}
int cmp(const void *a, const void *b) {return *((char *) a) - *((char *) b);
}
int main()
{int size;scanf("%s",str);while(str[len]!='\0'){len++;}//printf("%d\n",len);scanf("%d",&size);qsort(str, len, sizeof(char), cmp);int used[len];for(int i=0;i<len;i++)used[i]=0;backtracking(0,size,used);printf("%d",ansTop);return 0;
}(C卷,200分)- 田忌赛马
题目描述
给定两个只包含数字的数组a,b,调整数组 a 里面的数字的顺序,使得尽可能多的a[i] > b[i]。
数组a和b中的数字各不相同。
输出所有可以达到最优结果的a数组的结果。
输入描述
输入的第一行是数组 a 中的数字,其中只包含数字,每两个数字之间相隔一个空格,a数组大小不超过10。
输入的第二行是数组 b 中的数字,其中只包含数字,每两个数字之间相隔一个空格,b数组大小不超过10。
输出描述
输出所有可以达到最优结果的 a 数组的数量。
用例
输入 11 8 20
10 13 7
输出 1
说明 最优结果只有一个,a = [11, 20, 8],故输出1
输入 11 12 20
10 13 7
输出 2
说明 有两个a数组的排列可以达到最优结果,[12, 20, 11] 和 [11, 20, 12],故输出2
输入 1 2 3
4 5 6
输出 6
说明 a无论如何都会全输,故a任意排列都行,输出所有a数组的排列,6种排法。
题目解析
本题数量级不大,可以考虑暴力破解。即求解a数组的所有全排列,然后将a数组的每个全排列和b数组逐个元素进行比较,统计每个全排列中a[i] > b[i]的个数biggerCount。我们保留最大的Count 为 maxCount。
最终统计的是a[i] > b[i]的个数为maxCount的全排列的数量。
关于全排列的求解,可以参考:
添加链接描述
本题不需要我们输出具体排列,因此不用定义path记录全排列。
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 10
int a[MAX_SIZE];
int sizeA=0;
int b[MAX_SIZE];
int sizeB=0;
int maxcount=0;int ans=0;
void backtracking(int level,int* used,int count){if(level>=sizeA){if(count>maxcount){//找到最优结果maxcount=count;ans=1;}else if(maxcount==count){ans+=1;}return;}for(int i=0;i<sizeA;i++){if(used[i])continue;used[i]=1;backtracking(level+1,used,count+(a[i]>b[level]?1:0));used[i]=0;}}
int main()
{while(scanf("%d",&a[sizeA++])){if(getchar()!=' ')break;}while(scanf("%d",&b[sizeB++])){if(getchar()!=' ')break;}int used[MAX_SIZE]={0};backtracking(0,used,0);printf("%d",ans);return 0;
}相关文章:
- 字符串拼接、田忌赛马)
华为OD机试(C卷,200分)- 字符串拼接、田忌赛马
(C卷,200分)- 字符串拼接 题目描述 给定 M(0 < M ≤ 30)个字符(a-z),从中取出任意字符(每个字符只能用一次)拼接成长度为 N(0 < N ≤ 5)的字符串, 要求…...

Windows中配置python3.11环境安装教程
在Windows中配置Python 3.11环境的步骤如下: 第一步:下载 Python 3.11 访问 Python 官方网站:https://www.python.org/导航到 “Downloads” 部分,选择 “Windows”。在 “Windows” 页面中,找到 “Python 3.11.x”&…...

市场趋势的智能预测:Kompas.ai如何洞察未来市场动向
在商业领域,市场趋势预测是企业制定战略规划和做出明智决策的关键。准确把握市场动向能够帮助企业及时调整战略,抓住机遇,规避风险。Kompas.ai,一款先进的人工智能市场分析工具,正通过其深度学习和数据分析能力&#x…...

华南师范大学“大学生校外实践教学基地”授牌仪式暨见习参观活动圆满结束
为促进校企合作的深入发展,培育出具有实际应用技能的人才,7月9日,华南师范大学数学科学院与广东泰迪智能科技股份有限公司联合开展“大学生校外实践教学基地”授牌仪式暨见习参观活动。华南师范大学数学科学院数据科学系主任陈艳男、副主任陈…...

防爆定位信标适合工厂吗?都有哪些优势呢?
防爆定位信标产品可服务的范围非常广,尤其是具有一定危险性的岗位和行业,为了将损失降到最低或是说避免危险发生,一般都会安装这类产品,既是保护工作人员的人身安全,也能保护企业工厂的财产安全,因此这类设…...

行为模式8.状态模式------灯泡状态切换
行为型模式 模板方法模式(Template Method Pattern)命令模式(Command Pattern)迭代器模式(Iterator Pattern)观察者模式(Observer Pattern)中介者模式(Mediator Pattern…...

Linux账户和组管理——账户和工作组分类,用户账号文件,/etc/passwd文件中7个字段,id 命令
## 账户和工作组的分类 ### 用户分为三类: - 超级账户——账户名为root,它具有一切权限,只有进行系统维护(例如:建立用户等)或其他必要情形下才用超级用户登录,以避免系统出现安全问题。 - 系统账户——是Linux系统正常…...
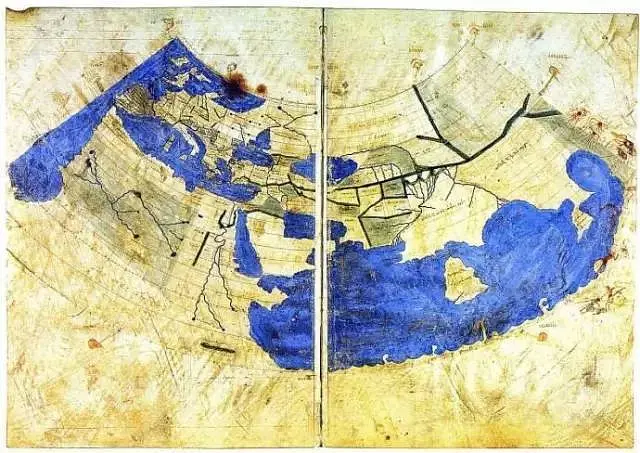
《大明混一图》: 令人叹为观止的古代世界地图
关注我们 - 数字罗塞塔计划 - 《大明混一图》是我国目前保存尺寸最大、最完整、年代最久远,且由中国人自己绘制的世界地图,2003年10月被列入《中国档案文献遗产名录》,现保存于中国第一历史档案馆。据学者们研究,这幅地图大约是…...

Java高级重点知识点-22-缓冲流、转换流、序列化流、打印流
文章目录 缓冲流字节缓冲流字符缓冲流 转换流InputStreamReader类OutputStreamWriter类 序列化ObjectOutputStream类ObjectInputStream类 打印流 缓冲流 缓冲流,也叫高效流,是对4个基本的 FileXxx 流的增强,所以也是4个流 基本原理: 缓冲流的…...

express民族民俗文化分享平台-计算机毕业设计源码22552
基于Vue的民族民俗文化分享平台设计与实现 摘 要 本文介绍了一种基于Vue.js前端框架和Express后端框架的民族民俗文化分享平台的设计和实现。该平台旨在通过线上方式,促进民族民俗文化的传播与分享,增强公众对多元文化的了解和认同。 平台为普通用户提供…...

Web 基础与HTTP 协议
域名的概述 (1 )域名的结构 (2 )域名结构类型 根域:指的是根服务器,要用来管理互联网的主目录,全世界只有13台。1个为 主根服务器,放置在美国。其余12 个均为辅根服务器,其中9个放置在美国;欧 洲2个&…...

C++超市外卖小程序-计算机毕业设计源码62482
摘要 随着社会生活节奏加快和消费习惯的变化,外卖服务成为人们日常生活中不可或缺的一部分。超市外卖作为新兴业态备受关注,然而传统外卖平台在推荐精准度和用户体验方面存在挑战。 本研究旨在基于协同过滤算法,结合C语言和MySQL数据库&#…...
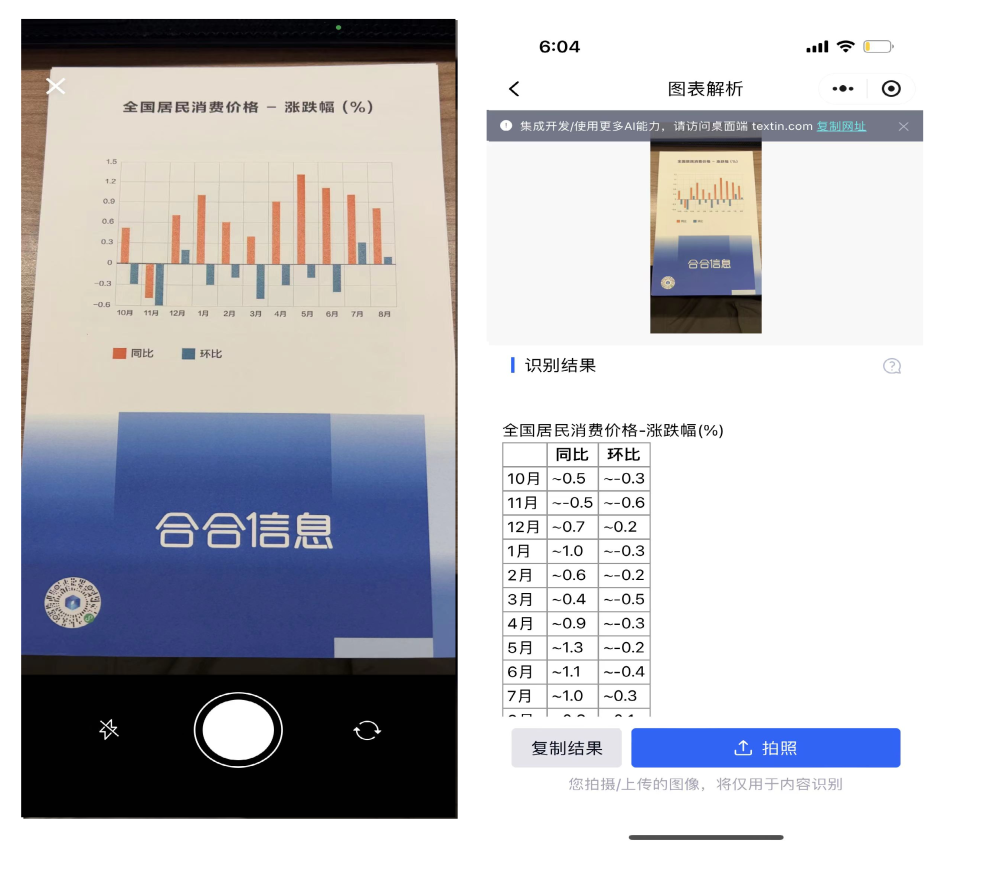
合合信息“大模型加速器”亮相2024世界人工智能大会
文章目录 📑引言一、大模型发展的挑战数据稀缺问题 二、大模型“加速器”解决方案概述文档解析引擎的特征 三、文档解析引擎的优势3.1 高速处理能力3.2 智能理解文档结构3.3 多种数据类型支持3.4 高精度数据提取3.5 应用广泛,适应性强 四、复杂图表解析4…...

2024.07.03校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、提前批 | 中国兵器工业集团第二〇二研究所 | 提前批/招/聘暨/暑期/开放日 提前批 | 中国兵器工业集团第二〇二研究所 | 提前批招聘暨暑期开放日 2、夏令营 | 2024年南网数字集团“未来…...

MySQL中的DDL语句
第一题 输入密码登录mysql,创建数据库zoo,转换到zoo数据库, mysql> create database zoo character set gbk; mysql> use zoo查看创建数据库zoo信息 mysql> show create database zoo;删除数据库zoo mysql> drop database zo…...

ENSP-防火墙小实验
实验总要求 我的拓扑图: 具体配置 1.交换机 vlan: # sysname Lswl # vlan batch 2 to 3 # 接口: [LSWl]int e 0/0/2 [LSWl-Ethernet0/0/2ldisplay this # interface Ethernet0/0/2port link-type accessport default vlan 2 # return [LsWl-Ethernet0…...

PHP微信小程序视频图文流量主变现小程序系统源码
💰微信小程序新机遇!视频图文流量主变现秘籍🔑 🚀【流量变现新风口】🚀 还在为微信小程序的庞大流量如何转化为真金白银而苦恼吗?今天,就带你揭秘“微信小程序视频图文流量主变现小程序”的神…...
PHP智慧社区小区物业管理系统小程序源码
让生活更便捷,社区更和谐✨ 🏡【开篇:智慧生活,从社区开始】🏡 在快节奏的现代生活中,寻找一份便捷与舒适成为了我们共同的追求。小区,作为我们日常生活的温馨港湾,其管理水平和服…...

手撸俄罗斯方块(五)——游戏主题
手撸俄罗斯方块(五)——游戏主题 当确定游戏载体(如控制台)后,界面将呈现出来。但是游戏的背景色、方块的颜色、方框颜色都应该支持扩展。 当前游戏也是如此,引入了 Theme 的概念,支持主题的扩…...

【测试开发】--安全渗透测试
1. 安全渗透 1.1 分类 web数据库安全web应用服务器安全(文件上传漏洞、文件包含漏洞)web客户端安全(XSS跨站攻击) 2. sql注入 2.1 sql注入介绍 sql注入在安全问题中排行榜首sql注入攻击是输入参数未经过滤,然后直…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

MTK-Android12-13 Camera2 设置默认视频画质功能实现
MTK-Android12-13 Camera2 设置默认视频画质功能实现 场景:部分客户使用自己的mipi相机安装到我们主板上,最大分辨率为1280720,但是视频画质默认的是640480。实际场景中,在默认视频分辨率情况下拍出来的视频比较模糊、预览也不清晰…...

交易系统开发:跨境资本的高速通道架构解密
连接纽约、香港与内陆的金融管道工程 总收益互换(TRS)在港美股投资中扮演着跨境资本流动的“隐形桥梁”。本文基于真实跨境券商系统开发实践,深入解析支持多市场、多币种、多通道的TRS平台架构设计与业务解决方案。 一、港美股TRS的核心价值&…...

1.springmvc基础入门(一)
1.Spring MVC概念 Spring MVC 是 Spring Framework 提供的 Web 组件,全称是 Spring Web MVC,是⽬前主流的实现 MVC 设计模式的框架,提供前端路由映射、视图解析等功能。 Java Web 开发者必须要掌握的技术框架。 2.Spring MVC 功能 MVC&am…...

gem5-gpu教程 在gem5-gpu上运行多个应用程序
问题一、gem5-gpu是否能够在系统调用仿真中同时运行两个不同的应用程序,一个在CPU上,另一个在gpu上。如果是这样,我该怎么做?我查看了配置和帮助文件,没有找到明确的方法。看起来rodinia基准测试使用CPU在GPU内核中启动工作,CPU内核在GPU执行时几乎处于空闲状态。这里的另…...
