特征值究竟体现了矩阵的什么特征?
特征值究竟体现了矩阵的什么特征?
简单来说就是x经过矩阵A映射后和自己平行
希尔伯特第一次提出eigenvalue,这里的eigen就是自己的。所以eigenvalue也称作本征值
特征值和特征向量刻画了矩阵变换空间的特征
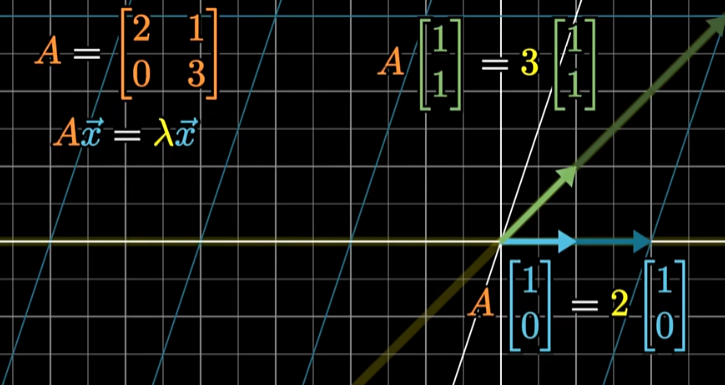
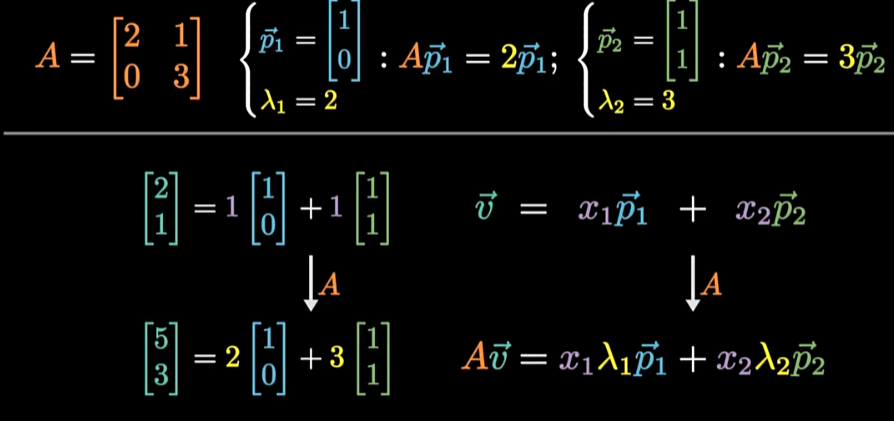
对平面上的任意向量可以如法炮制,把他在特征向量的坐标系下分解。分别在每个轴上伸缩,再用平行四边形法则加起来。就可以轻松确定任何一个向量被映射后到底在哪里。
可以说,矩阵特征向量的变化很好的描述了矩阵对空间的影响
将以上总结为3步
-
把向量分解为特征向量的线性组合
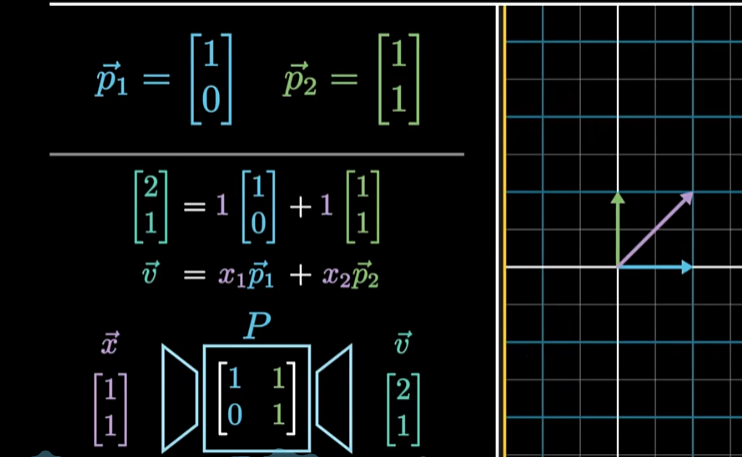
-
根据特征值分别缩放每个特征向量,两个特征值分别是2和3,所以两个系数就变成了两倍和三倍
-
重新将这些特征向量组合起来,将变换后的这些组合的系数向量使用线性映射P再变回去,就得到了原始空间的最终结果
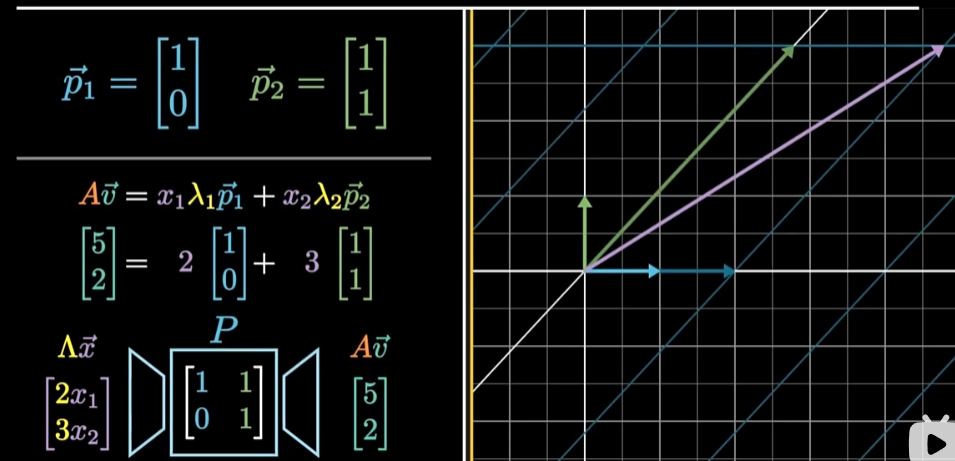
经过以上3步就得到了A作用于一个向量映射的整个过程。
我们为什么要费这么大的劲求这个分解呢?
- 计算简便
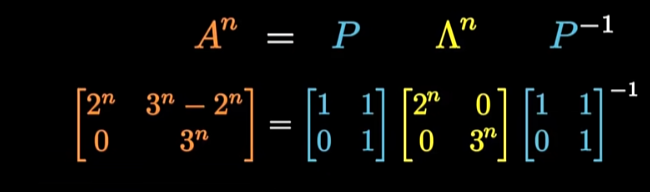
其中求特征值,利用特征多项式来求
线性空间当中几乎所有向量,经过某个线性映射的反复迭代以后,都会趋近于特征值最大的一个方向。
为什么要讲相似矩阵?
P这个矩阵承担着两个视角(默认视角和特征向量视角)之间的转换。
使用不同的视角来观察同一个线性映射。会得到不同的矩阵,于是这些矩阵叫做相似矩阵
头尾两个矩阵,就是这两个视角的转移矩阵
这个映射具有的性质,就被所有能够用相似变换所观察到的其他矩阵所共有。在某些方向上,方向不变时,伸长的倍数是保持的。这就是为什么**所有相似矩阵,他们特征值的集合是一样的。**而特征向量不一样
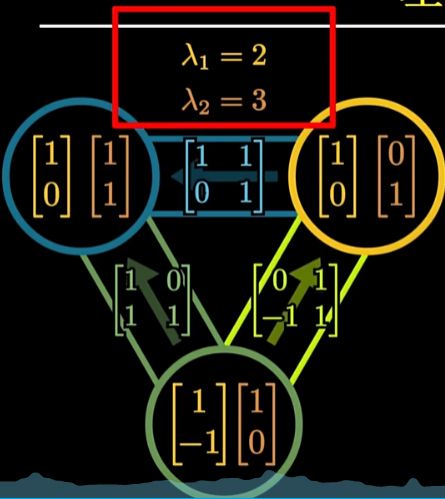
在特征向量的视角下,矩阵的迭代累乘变得特别简单,才使得我们可以用特征分解快速的计算出一个矩阵的幂次
一些结论
1.矩阵所有特征值的乘积等于行列式
2.几何重数不会超过代数重数
视频链接:
https://www.bilibili.com/video/BV1TH4y1L7PV/?spm_id_from=333.788&vd_source=8272bd48fee17396a4a1746c256ab0ae
相关文章:

特征值究竟体现了矩阵的什么特征?
特征值究竟体现了矩阵的什么特征? 简单来说就是x经过矩阵A映射后和自己平行 希尔伯特第一次提出eigenvalue,这里的eigen就是自己的。所以eigenvalue也称作本征值 特征值和特征向量刻画了矩阵变换空间的特征 对平面上的任意向量可以如法炮制,把他在特征…...

C语言-顺序表
🎯引言 欢迎来到HanLop博客的C语言数据结构初阶系列。在这个系列中,我们将深入探讨各种基本的数据结构和算法,帮助您打下坚实的编程基础。本次我将为你讲解。顺序表(也称为数组)是一种线性表,因其简单易用…...

OpenCV漫水填充函数floodFill函数的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 功能描述 ffloodFill函数是OpenCV库中用于图像处理的一个功能,它用于填充与种子点颜色相近的连通区域。这个函数在很多场景下都非常有用&#x…...

redis内存分析
阿里云redis集群对key进行hash后保存在对应的后端节点,使每个节点的key数量大致相同,但是如果存在大key,就会导致单个节点内存用满,可以使用redis-rdb-tools 或rdr来对内存进行分析。 redis-rdb-tools redis-rdb-tools通过对dum…...

redis批量删除keys,用lua脚本。
文章目录 现象解决方法 现象 系统报错: misconf redis is configured to save ....后查看机器内存。 是内存满了,需要删除其中的key 解决方法 (1) 编写一个脚本,放在redis-cli.exe同一个目录 (2) 脚本内容如下: -- 使用Lua脚…...

Python-找客户软件
软件功能 请求代码: 填充表格: 可以search全国各个区县的所有企业信息,过滤手机号、查看是否续存/在业状态。方便找客户。 支持定-制-其他引-留-阮*件(XHSS,DYY,KS,Bi-li*Bi-li) V*…...

STM32 - PWR 笔记
PWR(Power Control)电源控制 PWR 负责管理 STM32 内部的电源供电部分,可以实现 可编程电压监测器 和 低功耗模式 的功能 可编程电压监测器(PVD)可以监控VDD电源电压,当VDD下降到PVD阀值以下或上升到PVD…...

标准盒模型和怪异盒子模型的区别
在 CSS 中,标准盒模型和怪异盒模型是两种不同的盒子模型计算方式,主要区别如下: 一、标准盒模型(content-box) 1. 定义与组成 - 标准盒模型是 CSS 中默认的盒模型。 - 它由内容区域(content)、…...

推荐算法——MRR
定义: MRR计算的是第一个正确答案的排名的倒数,并对所有查询取平均值。它衡量了模型在排序结果中快速找到正确答案的能力。 其中: Q 是查询的总数。ranki 是第 i 个查询中第一个正确答案的排名(位置)。如果第一个正…...

idea中打开静态网页端口是63342而不是8080
问题: 安装了tomcat 并且也配置了环境,但是在tomcat下运行,总是在63342下面显示。这也就意味着,并没有运行到tomcat环境下。 找了好几个教程(中间还去学习了maven,因为跟的教程里面,没有maven,但…...

Vue3框架搭建3:配置说明-prettier配置
1、配置说明: .prettierrc.json{"$schema": "https://json.schemastore.org/prettierrc","semi": false,"tabWidth": 2,"singleQuote": true,"printWidth": 100,"trailingComma": "no…...
)
SQL MySQL定时器/事件调度器(Event Scheduler)
事件调度器(Event Scheduler)在MySQL数据库系统中是一个强大的功能组件,它允许用户定义一系列称为“事件”的数据库对象,这些事件在指定的时间或时间间隔自动执行预定义的SQL语句或操作。事件调度器通过维护一个时间计划表来管理这…...

从0到1构建渠道运营体系:实战案例与策略指南
引言 在当今竞争激烈的市场环境中,有效的渠道运营是企业实现产品或服务快速触达目标用户、提升市场份额的关键。从零开始构建一个高效的渠道运营体系,不仅需要深思熟虑的策略规划,还需要灵活应变的实战操作。本文将结合实战案例,…...
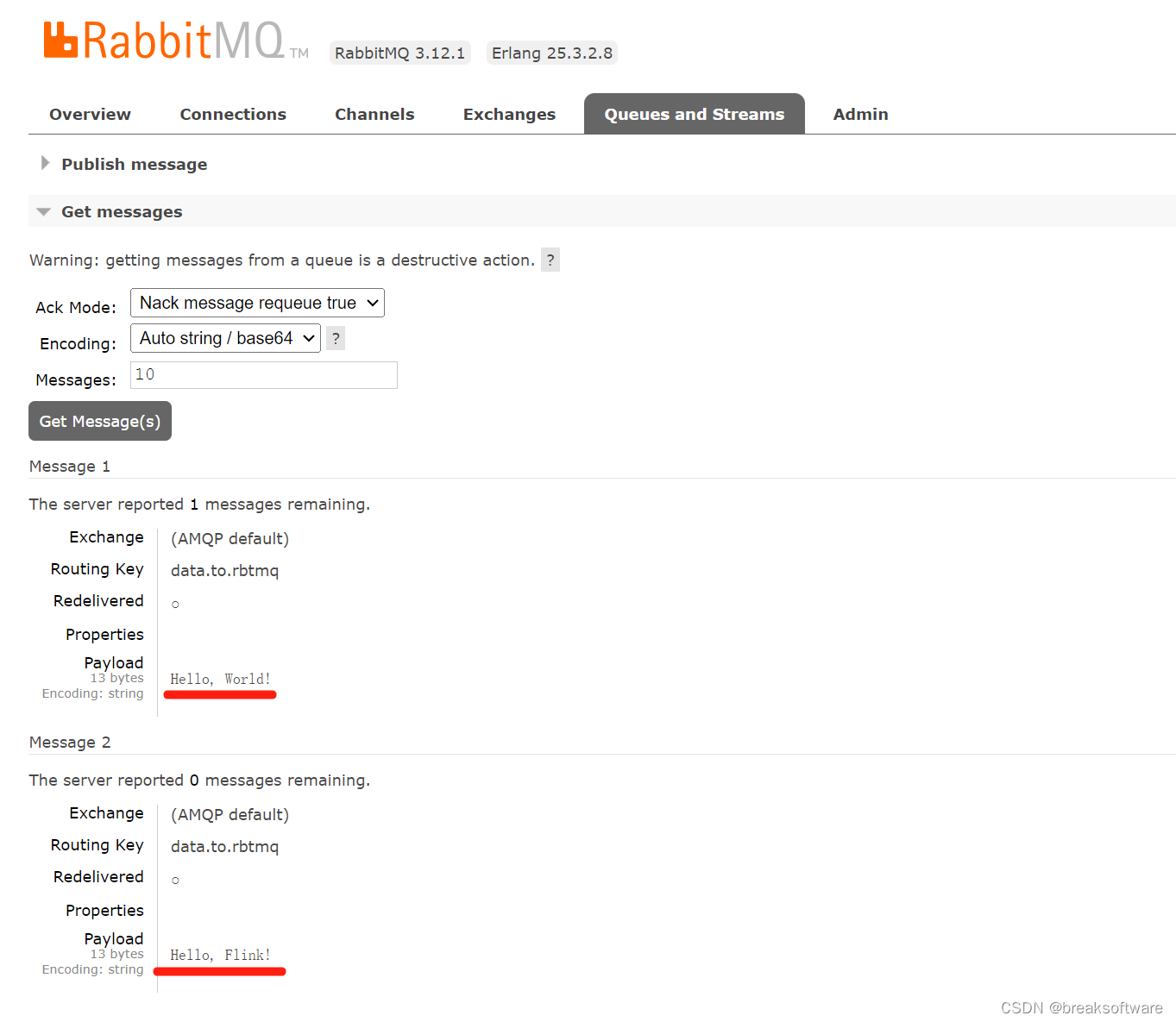
Java版Flink使用指南——将消息写入到RabbitMQ的队列中
大纲 新建工程新增依赖 编码自动产生数据写入RabbitMQ 测试工程代码 在 《Java版Flink使用指南——从RabbitMQ中队列中接入消息流》一文中,我们介绍了如何使用Java在Flink中读取RabbitMQ中的数据,并将其写入日志中。本文将通过代码产生一些数据…...

python excel openpyxl
python excel LTS 在开始之前,确保已经安装了 Python 和所需的库。 主要使用以下库: openpyxl:用于读取和写入 Excel 文件。 pandas:用于数据处理和分析。 xlwings:用于将 Python 与 Excel 连接,实现双向…...
)
C++八股(一)
目录 一、new和malloc ⭐ 二、class和struct的区别 ⭐ 三、char和int之间的转换 四、什么是野指针和悬挂指针 ⭐ 五、NULL和nullptr区别⭐ 六、指针常量和常量指针有何区别⭐ 七、物理内存和虚拟内存的区别⭐ 八、重载、重写和隐藏的区别⭐ 九、简述面向对象(OOP)的…...

【Git的基本操作】版本回退 | 撤销修改的三种情况 | 删除文件
目录 5.版本回退 5.1选项hard&后悔药 5.2后悔药&commit id 5.3版本回退的原理 6.撤销修改 6.1情况一 6.2情况二 6.3情况三 7.删除文件 Git重要能力之一马,版本回退功能。Git是版本控制系统,能够管理文件历史版本。本篇以ReadMe文件为…...

STM32-I2C
本内容基于江协科技STM32视频学习之后整理而得。 文章目录 1. I2C通信1.1 I2C通信简介1.2 硬件电路1.3 I2C时序基本单元1.3.1 起始条件和终止条件1.3.2 发送一个字节1.3.3 接收一个字节1.3.4 发送应答和接收应答 1.4 I2C时序1.4.1 指定地址写1.4.2 当前地址读1.4.3 指定地址读…...

04.ffmpeg打印音视频媒体信息
目录 1、相关头文件 2、相关结构体 3、相关函数 4、函数详解 5、源码附上 1、相关头文件 #include <libavformat/avformat.h> 包含格式相关的函数和数据结构 #include <libavutil/avutil.h> 包含一些通用实用函数 2、相关结构体 AV…...

微信开发授权登录梳理总结
授权登录流程对比 微信公众号/网页 微信文档地址:https://developers.weixin.qq.com/doc/offiaccount/OA_Web_Apps/Wechat_webpage_authorization.html 流程图如下: 特殊说明: 步骤1拼接的微信地址是:https://open.weixin.qq…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
