《算法笔记》总结No.6——贪心

一.简单贪心
贪心法是求解一类最优化问题的方法,它总是考虑在当前状态下局部最优(或较优)之后,来使全局的结果达到最优(或较优)的策略。显然,如果采取较优而非最优的策略(最优策略可能不存在或是不易想到),得到的全局结果也无法是最优的。而要获得最优结果,则要求中间的每步策略都是最优的,因此严谨使用贪心法来求解最优化问题需要对采取的策略进行证明。证明的一般思路是使用反证法及数学归纳法,即假设策略不能导致最优解,然后通过一系列推导来得到矛盾,以此证明策略是最优的,最后用数学归纳法保证全局最优。不过对平常使用来说,也许没有时间或不太容易对想到的策略进行严谨的证明(贪心的证明往往比贪本身更难),因此一般来说,如果在想到某个似乎可行的策略之后,并且自己无法举出反例,那么就勇敢地实现它。
1.组个最小数
给定数字0~9各若干个,可以任意顺序排列这些数字,但必须全部使用,且使目标数字尽可能小(当然0不能做首位)比如输入两个0、两个1、三个5和一个8,得到的最小数字就是100155858。
相信大家一下子就可以看出来策略:先从1~9中选择不为0的最小数输出,然后从0~9输出数字,每个数字输出次数为其剩余个数。
策略正确的证明:
- 首先由于所有数字都必须参与组合,因此最后结果的位数是确定的。
- 由于最高位不为0,则选一个尽可能小的数作为首位——最高位定理
- 其余位数也应该从小到大输出~
教材上的实在是太抽象了,好像有点错误,这里博主自己写了一种:
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;int main() { vector<int> V;for(int i=1;i<=10;i++){int temp=0;cin>>temp;V.push_back(temp);}sort(V.begin(),V.end()); //直接排成升序 int flag=0; //标记 for(int i=0;i<=9;i++)if(V[i]!=0){int temp=V[i];V[i]=V[0];V[0]=temp;flag=i;//保存第一个不为0的位置 break; }for(int i=flag+1;i<=9;i++) //找更小的头,直接从flag下一位开始即可,节省时间~ if(V[i]<V[0]&&V[i]!=0){int temp=V[i];V[i]=V[0];V[0]=temp;}for(int i=0;i<=9;i++)cout<<V[i];
}逻辑上没什么难度,主要是要想清楚~
2.月饼库存
- 输入:第一行输入N和M:N位月饼的种类数目,M位市场对月饼的需求总量;接下来的两行均要输入N个数:第一行的N个数分别对应当前种类的月饼全部卖出后可以挣多少,而第二行的N个数对应当前月饼的总数量~
- 要求输出:在规定需求量下最高收入
试想一下你如果作为老板,会怎么去“贪得无厌”?很明显——只需要在有限的需求量中,尽可能多的卖出单价最贵的月饼,岂不是可以收货最多的营业额?如下博主自己写的一种实现,和教材上的也不太一样:
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;struct mooncake{double num; //总数 double income; //总收入 double price; //单价,需要自己计算
}; int main() {int N,M;cin>>N>>M;vector<mooncake> V;for(int i=1;i<=N;i++) {mooncake temp;V.push_back(temp);}cout<<"请输入数量:"<<endl;for(int i=1;i<=N;i++) {double num=0;cin>>num;V[i-1].num=num;}cout<<"请输入总价:"<<endl;for(int i=1;i<=N;i++) {double income=0;cin>>income;V[i-1].income=income;}for(int i=0;i<=N-1;i++) V[i].price=V[i].income/V[i].num; //计算单价//按单价降序排列!保证贵的尽可能多卖for(int i=0;i<=V.size()-1;i++){for(int j=i;j<=V.size()-1;j++) if(V[j].price>V[i].price) {mooncake temp;temp=V[j];V[j]=V[i];V[i]=temp;}}for(int i=0;i<=V.size()-1;i++)cout<<"单价第"<<(i+1)<<"高的值为:"<<V[i].income<<" "<<V[i].price<<" "<<V[i].num<<endl;for(int i=0;i<=N-1;i++)cout<<V[i].num<<endl; int j=0; //使用的下标 double count=0; //总利润 while(M>0) //当还有需求量时 {double doubt=0;doubt=M-V[j].num; //用M减去当前类型的额总量 if(doubt>=0)//减了以后M还有剩余{M-=V[j].num;//当前种类全部卖出 count+=V[j].income;//直接总价相加 j++;cout<<V[j].num;}else if(doubt<0) //不够减这么多{count+=V[j].price*M;//剩余部分按照单价计算 break; } }cout<<"最高利润值为:"<<count<<endl;return 0;
}仔细品味上述中的whlie循环:当M还不为0时——即还有需求量,就卖最贵的月饼。按顺序一个一个卖:如果当前需求量足以卖完当前种类的全部数量,则直接累加总价;如果不足以卖完当前的全部,则有多少卖多少,按照单价计算即可~
我们拿教材的测试用例测试一下:
- 3 20
- 18 15 10
- 75 72 45

结果为94.50,和标准答案一致~
此外这里博主直接把排序写在main函数了,写在独立的函数再调用,对于结构体型的vector好像有点bug,排序不太成功,大家如果知道原因的话可以在评论区写出来~
二.区间贪心
题干如下:
 对于这类题目,只需要牢记——优先选择左端点大的区间!
对于这类题目,只需要牢记——优先选择左端点大的区间!

下面来说说为什么要这样做,如上图:不难发现,为了保证尽可能多选,当某个较长的区间包含了较短的区间,我们肯定要先选择最短的区间,这一点很好理解。

而对于上面这种情况,比如1和2这种重叠的区间,不难发现,如果选了左端点最大的1区间,只会占到9号位,而选了2号区间则会占到8号位——这显然不符合贪心尽可能少花钱(少花区间)的思想,因此要选得尽可能靠左,这样右边空的会更多~如上,我们手算可以看出来最多有4个不相交的。
教材上的代码:
#include <cstdio>
#include <algorithm>
using namespace std;const int maxn=110;
struct Inteval{int x,y; //开区间左右端点
}I[maxn]; bool cmp(Inteval a,Inteval b)
{if(a.x!=b.x)return a.x>b.x; //左端点从大到小排序 elsereturn a.y<b.y; //左端点相同的按右端点从小到大排序
}int main() {int n;while(scanf("%d",&n,n!=0)){for(int i=0;i<n;i++)scanf("%d%d",&I[i].x,&I[i].y);sort(I,I+n,cmp); //排序区间 int ans=1,lastX=I[0].x;//ans记录总数,lastX记录上一个被选择的区间的左端点 for(int i=1;i<n;i++){if(I[i].y<=lastX) //如果该区间右端点在lastX左边 {lastX=I[i].x; //以I[i]作为新选中的区间 ans++; //不相交的区间个数+1 } }printf("%d\n",ans); } return 0;
}不过博主还是不太喜欢原始数组,下面给一种vector结构体版本:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;struct section{int x=0;int y=0;//x和y分别为左右端点
}; int main() {int n=0;vector<section> V;cin>>n;for(int i=1;i<=n;i++) //读入数据 {section temp;int x=0,y=0;cin>>x>>y;if(x>y) //防止左端点大于右端点 {int temp1=x;x=y;y=temp1; }else if(x==y) //若左右端点相同 {i-=1; //则当前输入 不算cout<<"不可以输入相同的左右端点!"<<endl; continue; //舍弃数据,本次循环作废~ } temp.x=x;temp.y=y;V.push_back(temp);}//按要求排序区间优先级 for(int i=0;i<=V.size()-1;i++){for(int j=i+1;j<=V.size()-1;j++){if(V[j].x>V[i].x) //左端点越大越靠前{section temp=V[j];V[j]=V[i];V[i]=temp;}else if(V[j].x==V[i].x&&V[j].y<V[i].y) //左端点相同的话,右端点小的优先 {section temp=V[j];V[j]=V[i];V[i]=temp;} }}cout<<"顺序如下:"<<endl; for(int i=0;i<=V.size()-1;i++)cout<<V[i].x<<"~"<<V[i].y<<endl; int count=1,lastX=V[0].x;//count用来统计总数,lastX是上一个符合条件的区间的左端点for(int i=1;i<=V.size()-1;i++)//直接从第二个区间开始 {if(V[i].y<lastX) //如果当前区间的右端点不和上一个左端点相加,满足题意 {lastX=V[i].x;count++;} } cout<<count<<endl;return 0;
}测试如下:

总的来说,贪心法是用来解决一类最优化问题,并希望由局部最优策略来推得全局最优结果的算法思想。贪心算法适用的问题一定满足最优子结构的性质,即一个问题的最优解可以由他的子问题的最优解有效地构造出来。显然不是所有问题都适合贪心法,但是这并不妨碍贪心算法成为一个简洁、实用、高效的算法~
相关文章:

《算法笔记》总结No.6——贪心
一.简单贪心 贪心法是求解一类最优化问题的方法,它总是考虑在当前状态下局部最优(或较优)之后,来使全局的结果达到最优(或较优)的策略。显然,如果采取较优而非最优的策略(最优策略可能不存在或是不易想到),得到的全局结果也无法是…...
久期分析与久期模型
目录 一、久期分析的理论原理 二、数据准备 三、Stata 程序代码及解释 四、代码运行结果 一、久期分析的理论原理 久期(Duration)是衡量债券价格对利率变动敏感性的重要指标。它不仅仅是一个简单的时间概念,更是反映了债券现金流回收的平均…...

MybatisPlus 使用教程
MyBatisPlus使用教程 文章目录 MyBatisPlus使用教程1、使用方式1.1 引入依赖1.2 构建mapper接口 2、常用注解2.1 TableName2.2 TableId2.3 TableField MyBatisPlus顾名思义便是对MyBatis的加强版,但两者本身并不冲突(只做增强不做改变): 引入它并不会对原…...

bash: redi-cli: 未找到命令...
问题描述 在执行命令:redi-cli --bigkeys 提示:bash: redi-cli: 未找到命令... 确定服务器是否有Redis进程 ps -ef | grep redis查找Redis 文件信息 find / -name "redis-*"进入到当前目录 cd /usr/bin/再次执行命令 涉及redis-cli 连…...

linux 内核 红黑树接口说明
红黑树(rbtree)在linux内核中使用非常广泛,cfs调度任务管理,vma管理等。本文不会涉及关于红黑树插入和删除时的各种case的详细描述,感兴趣的读者可以查阅其他资料。本文主要聚焦于linux内核中经典rbtree和augment-rbtree操作接口的说明。 1、基本概念 二叉树:每个…...

【ELK】filebeat 和logstash区别
Filebeat 和 Logstash 都是 Elastic Stack (也称为 ELK Stack) 的重要组件,用于日志数据的收集、处理和传输。它们有不同的功能和使用场景: Filebeat 角色: 轻量级日志收集器。功能: 从指定的日志文件中读取日志数据。可以从多个源(如文件、…...

CNN -1 神经网络-概述
CNN -1 神经网络-概述 一:芯片科技发展介绍了解1> 芯片科技发展趋势2> 芯片使用领域3> 芯片介绍1. 神经网络芯片2. 神经网络处理单元NPU(Neural Processing Unit)二:神经网络1> 什么是神经网络2> 神经元3> 人工神经网络三:卷积神经网络(CNN)入门讲解一…...

插片式远程IO模块:Profinet总线耦合器在STEP7配置
XD9000是Profinet总线耦合器,单个耦合器最多可扩展32个I/O模块!本文将深入探讨插片式远程IO模块的应用,并揭秘Profinet总线耦合器在STEP7配置过程中的技巧与注意事项。 STEP7-MicroWINSMART软件组态步骤: 1、按照下图指示安装GSD…...

python3读取shp数据
目录 1 介绍 1 介绍 需要tmp.shp文件和tmp.dbf文件,需要安装geopandas第三方库,python3代码如下, import geopandas as gpdshp_file_path "tmp.shp" shp_data gpd.read_file(shp_file_path) for index, row in shp_data.iterro…...

pytorch实现水果2分类(蓝莓,苹果)
1.数据集的路径,结构 dataset.py 目的: 输入:没有输入,路径是写死了的。 输出:返回的是一个对象,里面有self.data。self.data是一个列表,里面是(图片路径.jpg,标签&…...

Redis实践经验
优雅的Key结构 Key实践约定: 遵循基本格式:[业务名称]:[数据名]:id例:login:user:10长度步超过44字节(版本不同,上限不同)不包含特殊字符 优点: 可读性强避免key冲突方便管理节省内存&#x…...

分类题解清单
目录 简介MySQL题一、聚合函数二、排序和分组三、高级查询和连接四、子查询五、高级字符串函数 / 正则表达式 / 子句 算法题一、双指针二、滑动窗口三、模拟四、贪心五、矩阵六、排序七、链表八、设计九、前缀和十、哈希表十一、字符串十二、二叉树十三、二分查找十四、回溯十五…...

QUdpSocket 的bind函数详解
QUdpSocket 是 Qt 框架中用于处理 UDP 网络通信的类。bind 函数是此类中的一个重要方法,它用于将 QUdpSocket 对象绑定到一个特定的端口上,以便在该端口上接收 UDP 数据包。 函数原型 在 Qt 中,bind 函数的原型通常如下所示: b…...
[spring] Spring MVC - security(下)
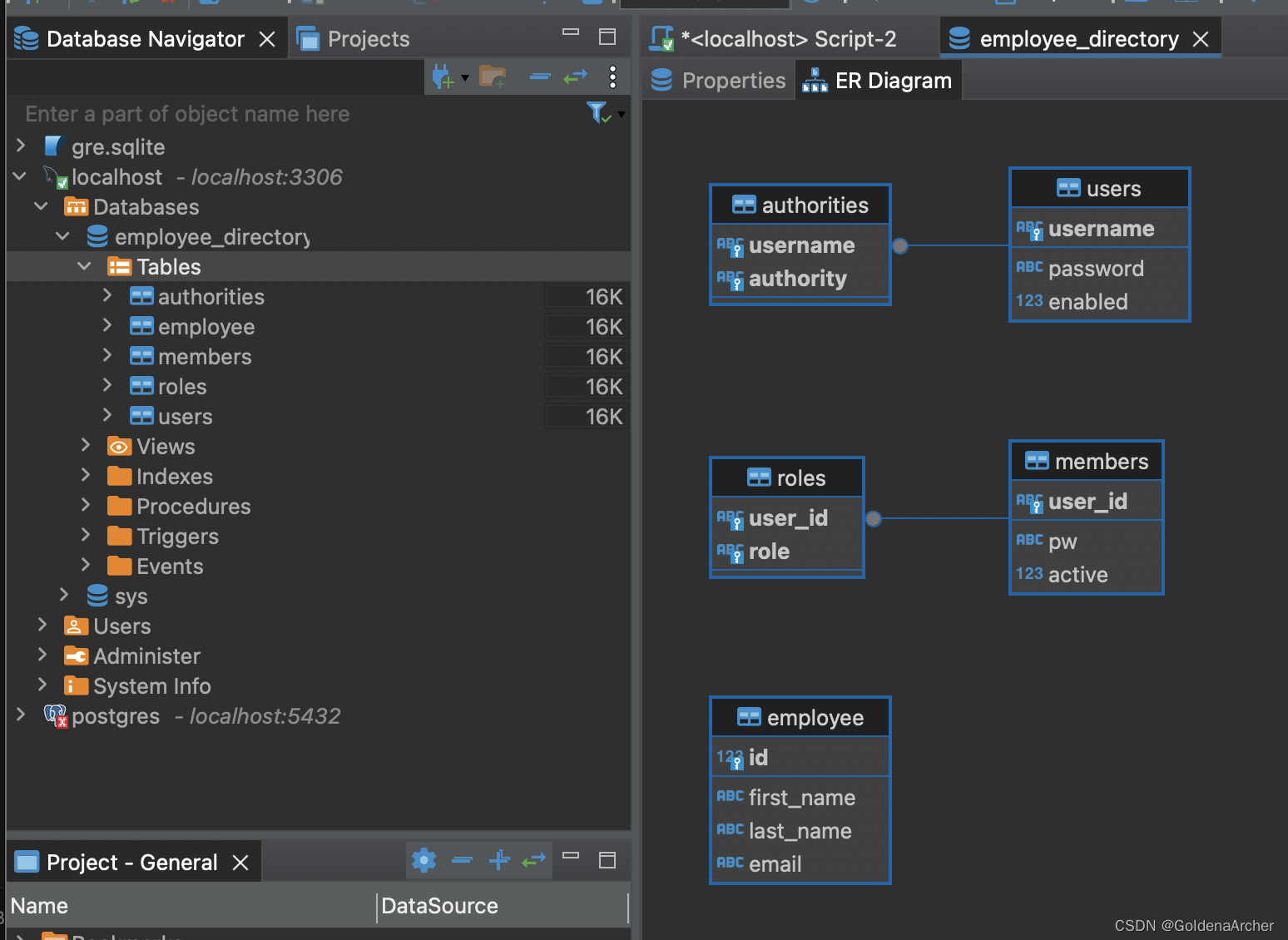
[spring] Spring MVC - security(下) callback 一下,当前项目结构如下: 这里实现的功能是连接数据库,大范围和 [spring] rest api security 重合 数据库连接 - 明文密码 第一部分使用明文密码 设置数据库 主要就是…...

数据库数据恢复—SQL Server数据库由于存放空间不足报错的数据恢复案例
SQL Server数据库数据恢复环境: 某品牌服务器存储中有两组raid5磁盘阵列。操作系统层面跑着SQL Server数据库,SQL Server数据库存放在D盘分区中。 SQL Server数据库故障: 存放SQL Server数据库的D盘分区容量不足,管理员在E盘中生…...

spring security的demo
参考: https://juejin.cn/post/6844903502003568647 Spring Security 5.7.0弃用 WebSecurityConfigurerAdapter-CSDN博客 创建 Spring Security 配置类 WebSecurityConfigurerAdapter已被弃用 package com.cq.sc.security.config;import org.springframework.c…...
无需构建工具,快速上手Vue2 + ElementUI
无需构建工具,快速上手Vue2 ElementUI 在前端开发的世界中,Vue.js以其轻量级和易用性赢得了开发者的青睐。而Element UI,作为一个基于Vue 2.0的桌面端组件库,提供了丰富的界面组件,使得构建美观且功能丰富的应用变得…...

通信协议_Modbus协议简介
概念介绍 Modbus协议:一种串行通信协议,是Modicon公司(现在的施耐德电气Schneider Electric)于1979年为使用可编程逻辑控制器(PLC)通信而发表。Modbus已经成为工业领域通信协议的业界标准(De f…...
LabVIEW优化氢燃料电池
太阳能和风能的发展引入了许多新的能量储存方法。随着科技的发展,能源储存和需求平衡的方法也需要不断创新。智慧城市倡导放弃石化化合物,采用环境友好的发电和储能技术。氢气系统和储存链在绿色能源倡议中起着关键作用。然而,氢气密度低&…...

SpringCloudGateway
作用 统一管理,易于监控安全,限流:在网关层就过滤掉非法信息nginx外部网关,gateway内网nginx可以使用Lua或Kong来增强 概念 id:名称随意uri: 被代理的服务地址。id和uri必填,谓词和过滤器非必填谓词:可以…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
