格密码学习笔记(六):格中模运算
文章目录
- 格中取模运算
- CVP和格的陪集
- 致谢
格中取模运算
定义(格的基本区域) P⊂Rn:{P+x∣x∈L}\mathcal{P} \subset \mathbb{R}^n : \{ \mathcal{P} + \bm{x} | \bm{x} \in \mathcal{L} \}P⊂Rn:{P+x∣x∈L}是Rn\mathbb{R}^nRn的一种划分。
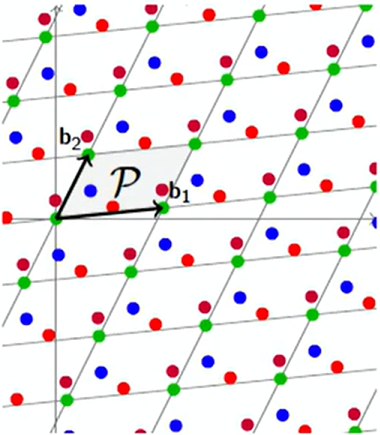
用P\mathcal{P}P对格点取模会呈现周期规律,即很多点“值”重复,例如上图中的绿色点为一组、红色点为一组、蓝色点为一组、棕色点为一组等。
- (L,+)(\mathcal{L}, +)(L,+)是(Rn,+)(\mathbb{R}^n, +)(Rn,+)的子群;
- 根据第1点可以构造商群Rn/L\mathbb{R}^n / \mathcal{L}Rn/L,念作RnmodL\mathbb{R}^n ~ \mathrm{mod} ~ \mathcal{L}Rn mod L;
- 对于Rn/L\mathbb{R}^n / \mathcal{L}Rn/L中的元素,与该元素同组的元素,共同构成一个陪集t+L\bm{t} + \mathcal{L}t+L;
- 格中每一个基本区域都提供了一套格和陪集的标准表示法。
商群和陪集的概念乍一看很迷惑,但其实很好理解,请参考文章
- 【群论入门】(5): 子群、陪集、正规子群与商群(收录于机器学习的数学基础)
- 商群 - 百度百科

注意: 这里格的基本区域P\mathcal{P}P取半开区域,以上图二维格为例,可以是左边界、下边界为闭边界,而右边界、上边界为开边界,这样格中的所有点就均只属于一个基本区域,即每个陪集在每个基本区域中也只有一个点。
- P=∑ibi⋅[0,1)≡Rn/L\mathcal{P} = \sum_i \bm{b}_i \cdot [0, 1) \equiv \mathbb{R}^n / \mathcal{L}P=∑ibi⋅[0,1)≡Rn/L。
由于对格进行取模,故t+L\bm{t} + \mathcal{L}t+L又可表示为(B∨)t(mod1)(\bm{B}^\vee) \bm{t} ~ (\mathrm{mod} ~ 1)(B∨)t (mod 1)。注意,由于t+L\bm{t} + \mathcal{L}t+L不在格上,故对偶空间基向量乘以该点结果不会是整数,除以1必然有小数部分,而这个小数部分可以独立地代表不同的商群。(个人疑问: 这里的mod\mathrm{mod}mod物理意义理解起来感觉怪怪的,为什么是小数部分?推测可能是计算机实际上没有整除这一功能,除以1还是会有小数部分;或者就是为了表示起来简单方便,用模1表示取小数部分)
如何求对偶格基上一篇文章给出了参考答案:格密码学习笔记(五):对偶格。
CVP和格的陪集
利用格陪集,CVP可以有另外一种定义方式。这里公开课视频讲得有点抽象,我尝试写笔记结合推测解释一下。
定义(CVP) 给定一个格陪集t+L\bm{t} + \mathcal{L}t+L,在该格陪集中找到距离原点最近的点。
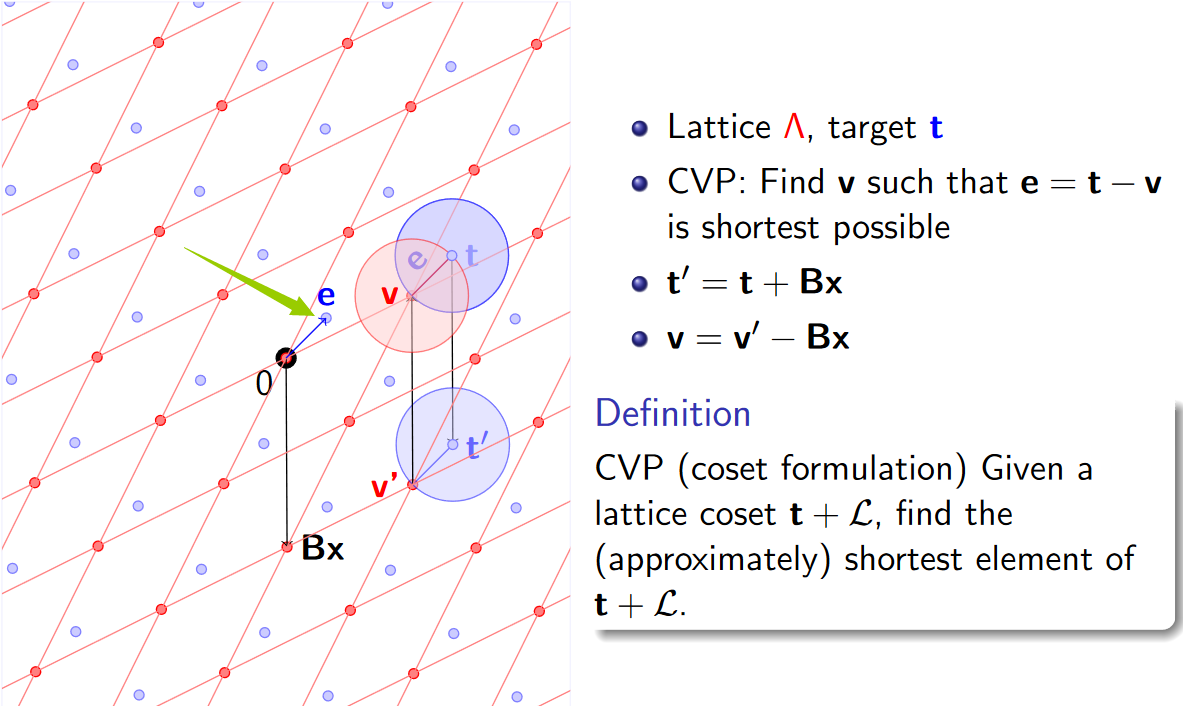
以上图为例,对于CVP给定的点t\bm{t}t,利用对偶格基相乘再模1可以获取陪集t+L\bm{t} + \mathcal{L}t+L中的所有点,即浅粉色的那部分点,找到距离原点最近的浅粉色点(绿色箭头所指),则t−e\bm{t} - \bm{e}t−e即CVP问题的解。
致谢
- Simons格密码公开课官网
Mathematics of Lattices - Simons Institute for the Theory of Computing - 哔哩哔哩中英双语视频(字幕组:重庆大学大数据与软件学院 后量子密码研究小组)
【中英字幕】Simons格密码讲座第1讲:格的数学定义_哔哩哔哩_bilibili - 其它格密码讲解课程和博文
Lattice学习笔记03:Dual Lattice(对偶格)
公开学习资料的无私奉献者
相关文章:

格密码学习笔记(六):格中模运算
文章目录格中取模运算CVP和格的陪集致谢格中取模运算 定义(格的基本区域) P⊂Rn:{Px∣x∈L}\mathcal{P} \subset \mathbb{R}^n : \{ \mathcal{P} \bm{x} | \bm{x} \in \mathcal{L} \}P⊂Rn:{Px∣x∈L}是Rn\mathbb{R}^nRn的一种划分。 用P\mathcal{P}P对…...

【C++】非常重要的——多态
凡是面向对象的语言,都有三大特性,继承,封装和多态,但并不是只有这三个特性,是因为者三个特性是最重要的特性,那今天我们一起来看多态! 目录 1.多态的概念 1.1虚函数 1.2虚函数的重写 1.3虚…...

发票账单很多?python助你批量完成数据提取
每天面对成堆的发票,无论是税务发票还是承兑单据,抑或是其他各类公司数据要从照片、PDF等不同格式的内容中提取,我们都有必要进行快速办公的能力提升。因此,我们的目标要求就十分明显了,首先要从图片中获取数据&#x…...

[闪存2.1] NAND FLASH特性串烧 | 不了解闪存特性,你能用好闪存产品吗?
前言 为了利用好闪存, 发挥闪存的优势, 以达到更好的性能和使用寿命, 那自然要求了解闪存特性。 闪存作为一种相对较新的存储介质, 有很多特别的特性。 一.闪存的特性 凡是采用Flash Memory的存储设备,可以统称为闪存存储。我们经常谈的固态硬盘(SSD),可以由volatile/…...

面试官问我按钮级别权限怎么控制,我说v-if,面试官说再见
最近的面试中有一个面试官问我按钮级别的权限怎么控制,我说直接v-if啊,他说不够好,我说我们项目中按钮级别的权限控制情况不多,所以v-if就够了,他说不够通用,最后他对我的评价是做过很多东西,但…...

阿里云服务器使用教程:CentOS 7安装nginx详细步骤
目录 1、下载nginx压缩包 2、配置nginx安装所需环境 3、解压nginx压缩包 4、编译安装nginx 5、nginx启动...

Android JNI浅析、Java和Native通信对象的传值和回调
简单了解一下jni JNI是一个本地编程接口,它允许运行在Java虚拟机的Java代码与用其他语言(如C,C和汇编)编写的库交互。 jni函数签名 首先看一下java类型对应的jni类型: Java类型符号BooleanZByteBCharCShortSIntILongJFloatFDo…...
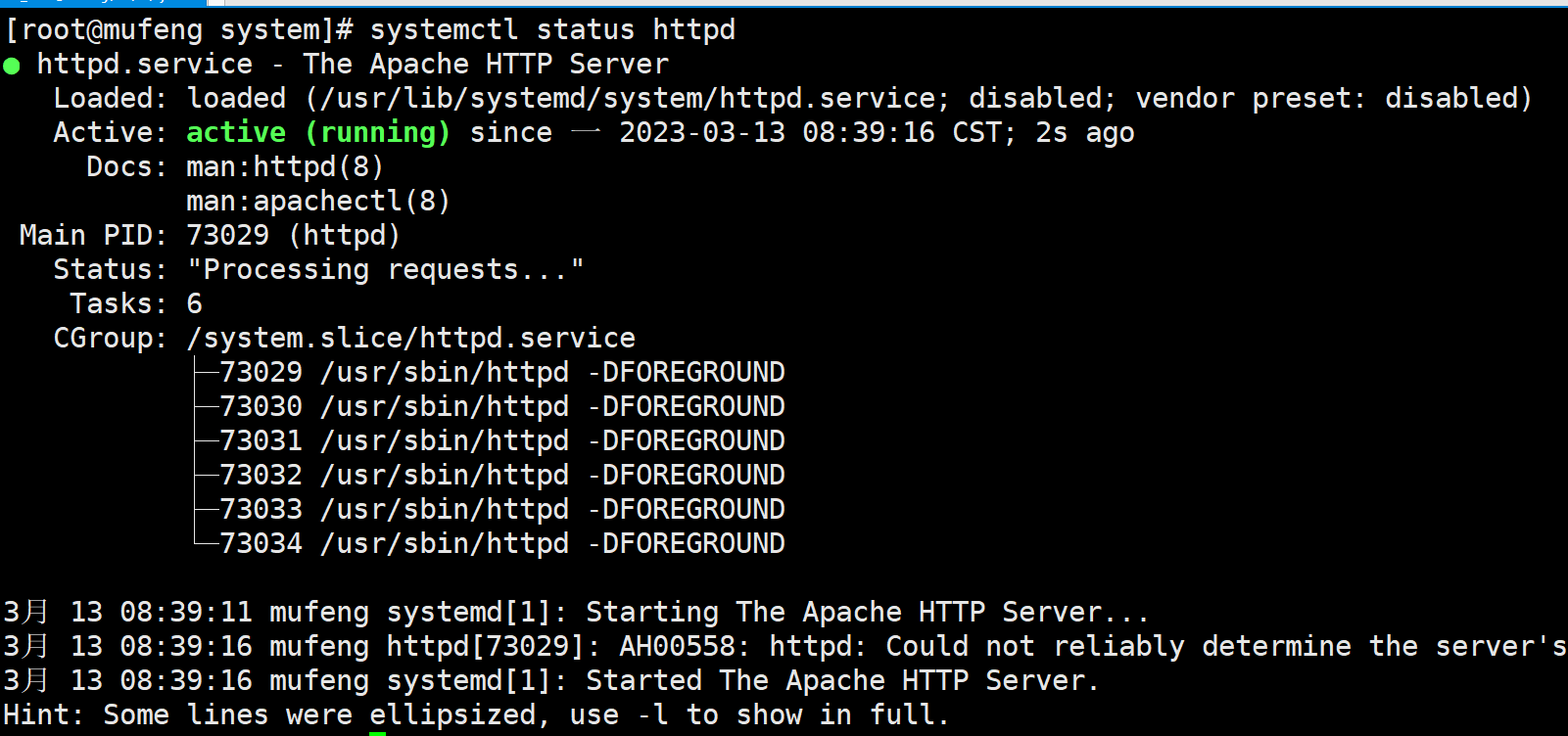
linux目录/usr/lib/systemd/system目录详解
文章目录前言一. systemd介绍二. service 脚本详解2.1 [Unit] 区块2.2 [Service] 区块2.3 [Install] 区块总结前言 init的进化经历了这么几个阶段: CentOS 5: SysV init,串行 CentOS 6:Upstart,并行,借鉴ubuntu CentOS 7:Syste…...

408考研计算机之计算机组成与设计——知识点及其做题经验篇目4:CPU的功能和基本结构
随着考研的慢慢复习,我们逐渐进入了计算机组成与设计的第五章中央处理器。它原名为CPU。姓C,名PU,字中央处理器,号计组难点,乃计算机之中心与核心部件,小编称之曰能算能控,赐名曰九天宏教普济生…...
等级考试试卷(五级)解析)
2022-12-10青少年软件编程(C语言)等级考试试卷(五级)解析
2022-12-10青少年软件编程(C语言)等级考试试卷(五级)解析T1、漫漫回国路 2020年5月,国际航班机票难求。一位在美国华盛顿的中国留学生,因为一些原因必须在本周内回到北京。现在已知各个机场之间的航班情况,求问他回不回得来(不考虑转机次数和机票价格)。 时间限制:10…...

刷题专练之链表(一)
文章目录前言一、 移除链表元素1.题目介绍2.思路3.代码二、反转链表1.题目介绍2.思路3.代码三、链表的中间结点1.题目介绍2.思路3.代码四、链表的中间结点1.题目介绍2.思路3.代码前言 以下是链表经常考的面试题,我在这里进行归纳和讲解,采取的是循序渐进…...

elasticsearch高级查询api
yml配置 #es配置 spring:elasticsearch:rest:uris: 192.168.16.188:9200添加依赖 <dependency><groupId>org.elasticsearch.client</groupId><artifactId>elasticsearch-rest-high-level-client</artifactId> </dependency>使用编程的形式…...

力扣-股票的资本损益
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1393. 股票的资本损益二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他…...

蓝桥杯刷题冲刺 | 倒计时26天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.路径2.特别数的和3.MP3储存4.求和1.路径 题目 链接: 路径 - 蓝桥云课 (lanqiao.cn…...

嵌入式软件开发之Linux 用户权限管理
目录 Ubuntu 用户系统 权限管理 权限管理命令 权限修改命令 chmod 文件归属者修改命令 chown Ubuntu 用户系统 Ubuntu 是一个多用户系统,我们可以给不同的使用者创建不同的用户账号,每个用户使用各自的账号登陆,使用用户账号的目的一是方便…...

2023-03-15 RabbitMQ
RabbitMQ整合 官网erlang版本 : 20.3.8.x 官方rabbitMq版本: rabbitmq-server-generic-unix-3.7.14.tar.xz 1.安装 1.1 安装erlang 1.安装环境 yum -y install make gcc gcc-c kernel-devel m4 ncurses-devel openssl-devel2.在/usr/local/下创建erlangapp文件…...
二叉树链式结构的实现
文章目录1.二叉树的遍历1.1前序、中序以及后序遍历1.2代码测试1.3层序遍历1.4二叉树遍历习题2.节点个数以及高度2.1二叉树节点个数2.2叶子节点个树2.3第k层节点个数2.4树的高度1.二叉树的遍历 1.1前序、中序以及后序遍历 学习二叉树结构,最简单的方式就是遍历。所…...

蓝桥杯刷题冲刺 | 倒计时28天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.卡片2.数字三角形3.购物单4.回文日期1.卡片 题目 链接: 卡片 - 蓝桥云课 (lanqiao…...

一文带你吃透操作系统
文章目录1. 进程、线程管理2. 内存管理3. 进程调度算法4. 磁盘调度算法5. 页面置换算法6. 网络系统7. 锁8. 操作系统知识点文章字数大约1.9万字,阅读大概需要65分钟,建议收藏后慢慢阅读!!!1. 进程、线程管理 进程和线程…...

计算机网络英文简称汇总
分类名词全拼汉译概述B2CBusiness-to-Consumer商对客概述P2PPeer-to-Peer对等概述C/SClient-Server服务器-客户机概述ITUInternational Telecommunication Union国际电信联盟概述IEEEInstitute of Electrical and Electronics Engineers电气与电子工程师协会概述ICCCInternatio…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
