【排序算法】归并排序

目录

一.基本思想

二.递归版本

三.非递归版本

四.特性总结

1.时间复杂度：O(N*logN)

2.空间复杂度：O(N)

3.稳定性：稳定

---

一.基本思想

归并排序是采用分治法的一个非常典型的应用。它将已经有序的序列合并为完全有序的序列，即先使得每一个子序列有序，再让子序列之间有序。归并排序建立在归并操作上，以下动图能很好的演示归并排序中归并的过程：

但上图只展示了归并排序中归并的过程，没有对拆分过程的展示，接下来我将具体介绍归并排序的核心步骤。

已知对于两个已经有序的序列而言，使用p1和p2来比较，p1和p2中较小的一个一定就是当前最小的，放入临时数组tmp中，随后指向的p向后移动，再次进行比较，如此就能将两个有序的序列合并为一个有序序列，这就做到了排序。

然而，如何得到两个已经有序的序列呢？这是类似问题，与排序整个序列的主问题是类似的，很明显，已经可以猜到要使用递归来实现了，那么只需要将两个无序序列进行再次拆分，直到序列中仅剩一个数据，那么此时就可以看作是有序的了，这就是拆分过程。 

拆分结束后，就进行归并，每两个已有序的序列合并到一起，再和其他已合并的序列进行合并，最终合并为一个序列，这就是排序后得到的最终结果，下图展示了整个过程：

 具体应该如何拆分？拆分也是有讲究的，不注意会产生问题。一般都会想到取中分割，取序列左端为begin,右端为end,mid自然等于(begin+end)/2，那么就可以围绕mid拆分为左右两个序列，其中mid应该包含在左端，否则会造成死循环，也就是应该分为[begin,mid]和[mid+1,end]，证明如下：

二.递归版本

//归并排序-主体
void _Merge(int* a, int* tmp, int begin, int end)
{//结束条件if (begin >= end)return;//拆分int mid = (begin + end) / 2;_Merge(a, tmp, begin, mid);_Merge(a, tmp, mid + 1, end);//归并int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}//归并排序
void Merge(int* a, int n)
{//创建临时数组int* tmp = (int*)malloc(sizeof(int) * n);_Merge(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}

三.非递归版本

对于非递归版本，就不用考虑拆分的过程了，直接将一个数组看作单个有序的状态开始归并。使用gap来模拟归并的过程，如下所示：

根据上述过程可以得到以下代码，但这样的写法却存在一些问题 ，不妨打印出来看看

//归并排序-主体-(非递归）
void Merge_NonR(int* a, int n)
{//创建临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}//gap控制每组归并的数据个数int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;printf("[%d %d],[%d,%d]", begin1, end1, begin2, end2);int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;printf("\n");}
}

 

可以很明显的看到，在只有10个数据的时候（有效下标为0到9），发生了数组越界的问题 ，那么这就还需要在程序中加入对应的解决方法，从上图可以发现，只要是begin2(上图的10和12）出现了越界（大于等于n）那么后一个序列就是非法的，也就不用归并了，此时可以直接跳出循环直接到下一个gap，那么到最后一轮，end2是越界的（如上图15）此时8到9是有序的，只需要调整end2为9(即n-1)即可。完整实现的代码如下：

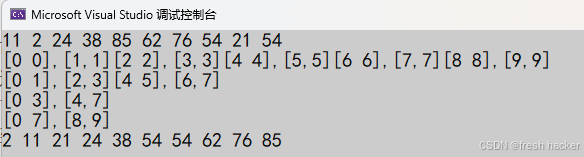
//归并排序-主体-(非递归）
void Merge_NonR(int* a, int n)
{//创建临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}//gap控制每组归并的数据个数int gap = 1;while (gap < n){for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;if (begin2 >= n)break;if (end2 >= n)end2 = n - 1;printf("[%d %d],[%d,%d]", begin1, end1, begin2, end2);int j = i;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;printf("\n");}
}

四.特性总结

1.时间复杂度：O(N*logN)

依据二分往下递归，类似于二叉树，总共有LogN层，每层总的归并合计起来可以看作O（N）,因此总的时间复杂度可以看作是：O(N*logN)

2.空间复杂度：O(N)

由于开辟了一个大小为N的额外数组，因此归并排序的空间复杂度为O(N)

3.稳定性：稳定