深度学习DeepLearning二元分类 学习笔记
文章目录
- 类别区分
- 变量与概念
- 逻辑回归
- Sigmoid函数
- 公式
- 决策边
- 逻辑损失函数和代价函数
- 逻辑回归的梯度下降
- 泛化
- 过拟合的解决方案
- 正则化
类别区分
变量与概念
| 决策边 | 置信度阈值threshold | 过拟合 | 欠拟合 |
|---|---|---|---|
| 正则化 | 高偏差 | lambda(λ) | |
线性回归受个别极端值影响,不适合用于分类
逻辑回归
-
输出值介于(0,1)
-
解决输出标签,判断真值
-
用于回归和分类
Sigmoid函数

图注:z越大,函数g(z)值越趋近于1;z为负数,越小则函数g(z)值越趋近于零。

公式
f w ⃗ , b = g ( w ⃗ ∗ x ⃗ + b ) = 1 1 + e − ( w ⃗ ∗ x ⃗ + b ) f_{\vec{w},b}=g(\vec{w}*\vec{x}+b)=\dfrac{1}{1+e^{-(\vec{w}*\vec{x}+b)}} fw,b=g(w∗x+b)=1+e−(w∗x+b)1
P ( y = 0 ) + P ( y = 1 ) = 1 P(y=0)+P(y=1)=1 P(y=0)+P(y=1)=1
一般写法: f w ⃗ , b ( x ⃗ ) = P ( y = 1 ∣ x ⃗ ; w ⃗ , b ⃗ ) f_{\vec{w},b}(\vec x)=P(y=1|\vec x;\vec w,\vec b) fw,b(x)=P(y=1∣x;w,b)
含义:w,b为影响因子的时候,选中x行向量时,y=1的概率是多少。
决策边

逻辑损失函数和代价函数
L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ) = − y ( i ) l o g ( f w ⃗ , b ( x ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) L(f_{\vec w,b}(\vec x^{(i)}),y^{(i)})=-y^{(i)}log(f_{\vec w,b}(x^{(i)}))-(1-y^{(i)})log(1-f_{\vec w,b}(\vec x^{(i)})) L(fw,b(x(i)),y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))
分取值写,则如下图:

负的log函数取零到一的部分。如上图。

平方误差代价函数不适用原因:会出现多个局部最小值。
简化的代价函数为 J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ L ( f w ⃗ , b ( x ⃗ ( i ) ) , y ( i ) ] J(\vec w, b)=-\dfrac{1}{m}\sum\limits_{i=1}^m[L(f_{\vec w,b}(\vec x^{(i)}),y^{(i)}] J(w,b)=−m1i=1∑m[L(fw,b(x(i)),y(i)]
它由极大似然估计法推出。
凸函数原因:凸优化学习
逻辑回归的梯度下降
重复地更新w和b,令其值为旧值-(学习率 α ∗ α * α∗ 偏导数项)
泛化
若一个模型能从从未见过的数据中做出准确的预测,我们说它能够从训练集泛化到测试集。我们的目标是构建一个泛化精度尽可能高的模型
一个模型不能太过特殊以至于只能用于一些数据,也不能过于宽泛难以拟合数据。


过拟合的解决方案
- 收集更多数据,但数据收集能力可能有上限。
- 观察是否可以用更少特征,应选用最相关特征,但有些被忽略的特征可能实际上有用。有些算法可以自动选择合适的特征。
- 正则化,w1到wn可以缩小以适应训练集,不推荐缩小b
正则化
一种惩罚,如果某一个w的增大使代价函数J增大,那它实际应该减小。
J ( w ⃗ , b ) = 1 2 m [ ∑ i = 1 m ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 + λ 2 m ∑ j = 1 n w j 2 + λ 2 m b 2 ] ( λ > 0 ) J(\vec w, b)=\dfrac{1}{2m}[\sum\limits_{i=1}^m(f_{\vec w, b}(\vec x^{(i)})-y^{(i)})^2+\dfrac{λ}{2m}\sum\limits_{j=1}^nw_j^2+\dfrac{λ}{2m}b^2](λ>0) J(w,b)=2m1[i=1∑m(fw,b(x(i))−y(i))2+2mλj=1∑nwj2+2mλb2](λ>0)
选择合适的λ以避免过拟合和欠拟合。

相关文章:

深度学习DeepLearning二元分类 学习笔记
文章目录 类别区分变量与概念逻辑回归Sigmoid函数公式决策边逻辑损失函数和代价函数逻辑回归的梯度下降泛化过拟合的解决方案正则化 类别区分 变量与概念 决策边置信度阈值threshold过拟合欠拟合正则化高偏差lambda(λ) 线性回归受个别极端值影响&…...

Eureka 介绍与使用
Eureka 是一个开源的服务发现框架,它主要用于在分布式系统中管理和发现服务实例。它由 Netflix 开发并开源,是 Netflix OSS 中的一部分。 使用 Eureka 可以方便地将新的服务实例注册到 Eureka 服务器,并且让其他服务通过 Eureka 服务器来发现…...

Java异常体系、UncaughtExceptionHandler、Spring MVC统一异常处理、Spring Boot统一异常处理
概述 所有异常都是继承自java.lang.Throwable类,Throwable有两个直接子类,Error和Exception。 Error用来表示程序底层或硬件有关的错误,这种错误和程序本身无关,如常见的NoClassDefFoundError。这种异常和程序本身无关࿰…...

bash终端快捷键
快捷键作用ShiftCtrlC复制ShiftCtrlV粘贴CtrlAltT新建终端ShiftPgUp/PgDn终端上下翻页滚动CtrlC终止命令CtrlD关闭终端CtrlA光标移动到最开始为止CtrlE光标移动到最末尾CtrlK删除此处到末尾的所有内容CtrlU删除此处至开始的所有内容CtrlD删除当前字符CtrlH删除当前字符的前一个…...

【Visual Studio】Visual Studio报错合集及解决办法
目录 Visual Studio报错:error LNK2001 Visual Studio报错:error C2061 Visual Studio报错:error C1075 Visual Studio报错:error C4430 Visual Studio报错error C3867 概述 持续更细Visual Studio报错及解决方法 Visual Studio报错:error LNK2001 问题 : error LNK2001…...

【微信小程序知识点】转发功能的实现
转发功能,主要帮助用户更流畅地与好友分享内容与服务。 想实现转发功能,有两种方式: 1.页面js文件必须声明onShareAppMessage事件监听函数,并自定义转发内容。只有定义了此事件处理函数,右上角菜单才会显示“转发”按…...

用python识别二维码(python实例二十三)
目录 1.认识Python 2.环境与工具 2.1 python环境 2.2 Visual Studio Code编译 3.识别二维码 3.1 代码构思 3.2 代码实例 3.3 运行结果 4.总结 1.认识Python Python 是一个高层次的结合了解释性、编译性、互动性和面向对象的脚本语言。 Python 的设计具有很强的可读性&…...
电脑文件夹怎么设置密码?让你的文件更安全!
在日常使用电脑的过程中,我们常常会有一些需要保护的个人文件或资料。为了防止这些文件被他人未经授权访问,对重要文件夹设置密码是一种有效的保护措施,可是电脑文件夹怎么设置密码呢?本文将介绍2种简单有效的方法帮助您为电脑文件…...

paddla模型转gguf
在使用ollama配置本地模型时,只支持gguf格式的模型,所以我们首先需要把自己的模型转化为bin格式,本文为paddle,onnx,pytorch格式的模型提供说明,safetensors格式比较简单请参考官方文档,或其它教…...

Memcached vs Redis——Java项目缓存选择
在Java项目开发中,缓存系统作为提升性能、优化资源利用的关键技术之一,扮演着至关重要的角色。Memcached和Redis作为两种流行的缓存解决方案,各有其独特的优势和应用场景。本文旨在通过分析项目大小、用户访问量、业务复杂度以及服务器部署情…...

大模型最新黑书:基于GPT-3、ChatGPT、GPT-4等Transformer架构的自然语言处理 PDF
今天给大家推荐一本丹尼斯罗斯曼(Denis Rothman)编写的关于大语言模型(LLM)权威教程<<大模型应用解决方案> 基于GPT-3、ChatGPT、GPT-4等Transformer架构的自然语言处理>!Google工程总监Antonio Gulli作序,这含金量不…...

【电子数据取证】电子数据司法鉴定
文章关键词:电子数据取证、司法鉴定服务、司法鉴定流程 一、定义 什么是司法鉴定? 在诉讼活动中鉴定人运用科学技术或者专业知识对诉讼涉及的专门性问题进行鉴别和判断并提供鉴定意见的活动。 电子数据司法鉴定 那么电子数据司法鉴定,就…...

使用 OpenCV 的 inRange 函数进行颜色分割
使用 OpenCV 的 inRange 函数进行颜色分割 在图像处理领域,颜色分割是一个常见的任务,常用于识别和提取图像中的特定颜色区域。OpenCV 提供了一个非常方便的函数 inRange 来实现这一功能。在这篇博客中,我们将详细介绍 inRange 函数的用法&a…...
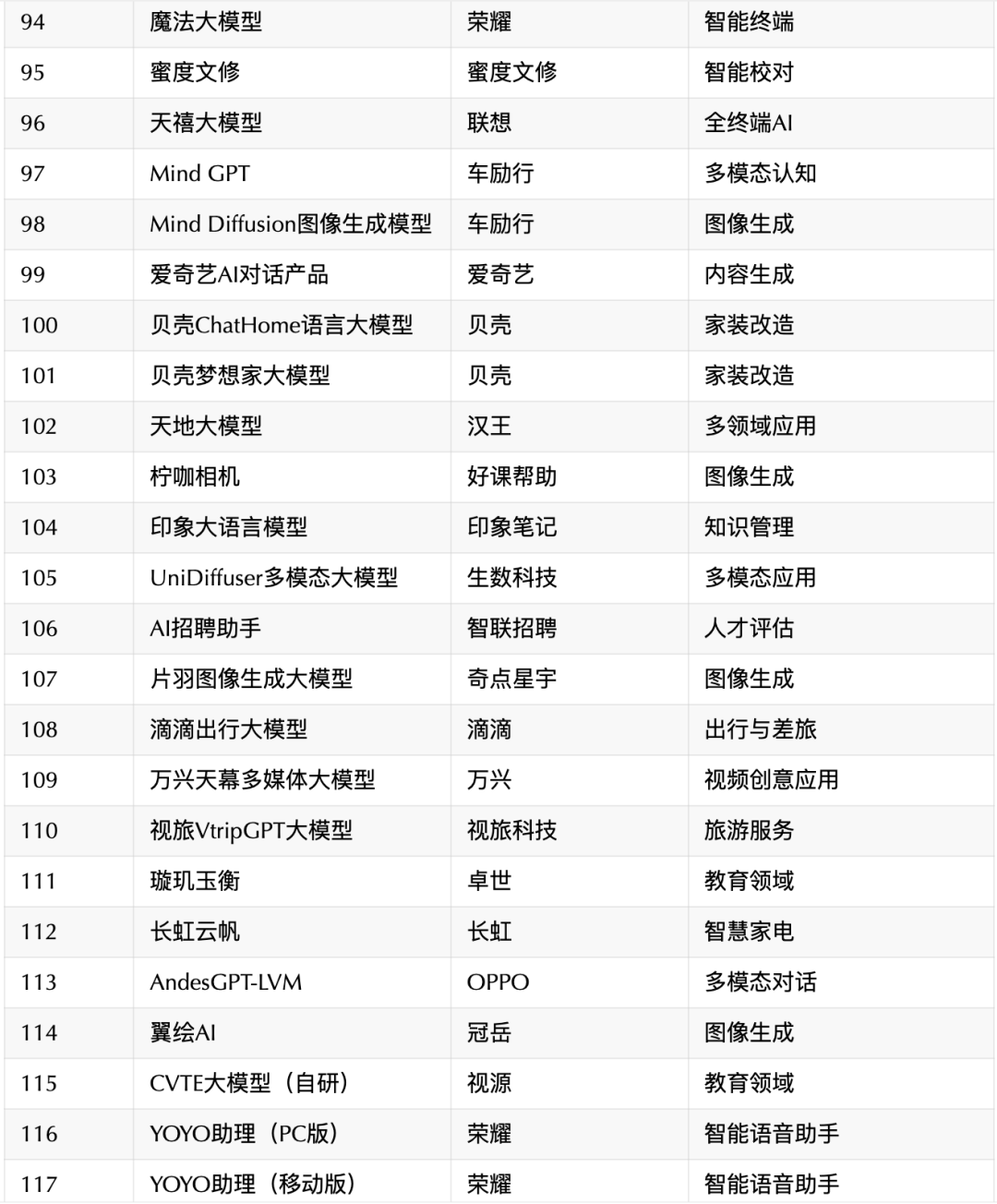
OpenAI终止对中国提供API服务,对国内AI市场产生重大冲击?
6月25日,OpenAI突然宣布终止向包括中国在内的国家地区提供API服务,本月9日这一政策已经正式生效了! 有人说,这个事件给中国AI行业带来很大冲击!是这样吗?在展开讨论前,我们先来看看什么是API服务…...

JavaDS —— 栈 Stack 和 队列 Queue
栈的概念 栈是一种先进后出的线性表,只允许在固定的一端进行插入和删除操作。 进行插入和删除操作的一端被称为栈顶,另一端被称为栈底 栈的插入操作叫做进栈/压栈/入栈 栈的删除操作叫做出栈 现实生活中栈的例子: 栈的模拟实现 下面是Jav…...

C++进阶:继承和多态
文章目录 ❤️继承🩷继承与友元🧡继承和静态成员💛菱形继承及菱形虚拟继承💚继承和组合 ❤️多态🩷什么是多态?🧡多态的定义以及实现💛虚函数💚虚函数的重写💙…...
(冒泡、快排、堆排、选择排序))
【八大排序】java版(上)(冒泡、快排、堆排、选择排序)
文章目录 一、冒泡排序(重点)思路代码 二、快排(面试重点)思路代码 三、堆排序(面试重点)思路代码 四、选择排序思路代码 一、冒泡排序(重点) 思路 前后两两数据进行比较,小的数据往前走,大的数据往后走,每一轮结束之后,最大的数…...

.Net Core 微服务之Consul(二)-集群搭建
引言: 集合上一期.Net Core 微服务之Consul(一)(.Net Core 微服务之Consul(一)-CSDN博客) 。 目录 一、 Consul集群搭建 1. 高可用 1.1 高可用性概念 1.2 高可用集群的基本原理 1.3 高可用集群的架构设计 1.3.1 主从复制架构 1.3.2 共享存储架构 1.3.3 负载均衡…...
)
C++ --> 类和对象(二)
前言 在前面简单的介绍了OOP,什么是类,在类中的this指针。接下来就深入理解类和对象。 默认成员函数 默认构造函数:用于在创建对象时初始化对象的成员变量。默认拷贝构造函数:用于使用已存在的对象来初始化新创建的对象。默认析构…...

利用宝塔安装一套linux开发环境
更新yum,并且更换阿里镜像源 删除yum文件 cd /etc/yum.repos.d/ 进入yum核心目录 ls sun.repo rm -rf * 删除之前配置的本地源 ls 配置阿里镜像源 wget -O /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-7.repo 配置扩展包 wge…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
