【VRP】基于常春藤算法IVY求解带时间窗的车辆路径问题TWVRP,最短距离附Matlab代码
% VRP - 基于IVY算法的TWVRP最短距离求解
% 数据准备
% 假设有一组客户点的坐标和对应的时间窗信息
% 假设数据已经存储在 coordinates、timeWindows 和 demands 变量中
% 参数设置
numCustomers = size(coordinates, 1); % 客户点数量
vehicleCapacity = 100; % 车辆容量
numVehicles = 5; % 车辆数量
% 构建距离矩阵
distanceMatrix = zeros(numCustomers+1, numCustomers+1); % +1是为了包含仓库点
for i = 1:numCustomers+1
for j = 1:numCustomers+1
distanceMatrix(i, j) = pdist([coordinates(i, 😃; coordinates(j, 😃], ‘euclidean’);
end
end
% IVY算法求解
bestDistance = Inf;
bestSolution = [];
for iter = 1:100 % 迭代次数
% 随机生成初始解
solution = cell(numVehicles, 1);
for k = 1:numVehicles
% 随机选择一个客户点作为起始点
startNode = randi(numCustomers) + 1; % +1是为了排除仓库点
% 初始化路径
path = [1, startNode, 1]; % 1代表仓库点
% 计算剩余容量
remainingCapacity = vehicleCapacity - demands(startNode);
% 随机构建路径
while remainingCapacity > 0
validNodes = setdiff(2:numCustomers+1, path); % 排除已经访问过的点
validDemands = demands(validNodes);
feasibleNodes = validNodes(validDemands <= remainingCapacity);
if isempty(feasibleNodes)
break;
end
nextNode = randsample(feasibleNodes, 1);
path = [path, nextNode];
remainingCapacity = remainingCapacity - demands(nextNode);
end
solution{k} = path;
end
% 评估解的距离
totalDistance = 0;
for k = 1:numVehiclespath = solution{k};for i = 1:length(path)-1totalDistance = totalDistance + distanceMatrix(path(i), path(i+1));end
end% 更新最优解
if totalDistance < bestDistancebestDistance = totalDistance;bestSolution = solution;
end
end
% 输出最优解距离和路径
disp(‘Best Distance:’);
disp(bestDistance);
disp(‘Best Solution:’);
for k = 1:numVehicles
disp(bestSolution{k});
end
相关文章:

【VRP】基于常春藤算法IVY求解带时间窗的车辆路径问题TWVRP,最短距离附Matlab代码
% VRP - 基于IVY算法的TWVRP最短距离求解 % 数据准备 % 假设有一组客户点的坐标和对应的时间窗信息 % 假设数据已经存储在 coordinates、timeWindows 和 demands 变量中 % 参数设置 numCustomers size(coordinates, 1); % 客户点数量 vehicleCapacity 100; % 车辆容量 numV…...

常用软件的docker compose安装
简介 Docker Compose 是 Docker 的一个工具,用于定义和管理多容器 Docker 应用。通过使用一个单独的 YAML 文件,您可以定义应用所需的所有服务,然后使用一个简单的命令来启动和运行这些服务。Docker Compose 非常适合于微服务架构或任何需要…...

Excel第28享:如何新建一个Excel表格
一、背景需求 小姑电话说:要新建一个表格,并实现将几个单元格进行合并的需求。 二、解决方案 1、在电脑桌面上空白地方,点击鼠标右键,在下拉的功能框中选择“XLS工作表”或“XLSX工作表”都可以,如下图所示。 之后&…...

计算机网络知识汇总
OSI七层模型 七层模型一般指开放系统互连参考模型,开放系统互连参考模型 (Open System Interconnect 简称OSI),OSI参考模型是具有7个层次的框架,自底向上的7个层次分别是物理层、数据链路层、网络层、传输层、会话层、…...
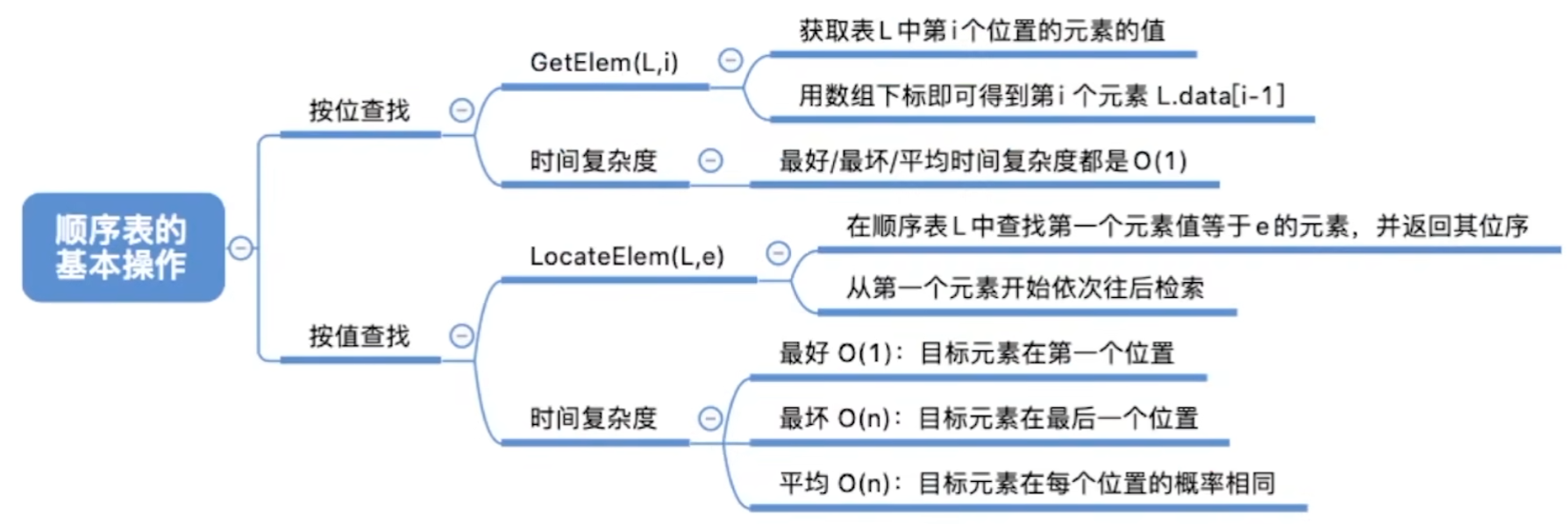
数据结构——考研笔记(二)线性表的定义和线性表之顺序表
文章目录 二、线性表2.1 定义、基本操作2.1.1 知识总览2.1.2 线性表的定义2.1.3 线性表的基本操作2.1.4 知识回顾与重要考点 2.2 顺序表2.2.1 知识总览2.2.2 顺序表的定义2.2.3 顺序表的实现——静态分配2.2.4 顺序表的实现——动态分配2.2.5 知识回顾与重要考点2.2.6 顺序表的…...

quota使用
一、检查系统是否支持 grep CONFIG_QUOTA /boot/config* CONFIG_QUOTAy CONFIG_QUOTA_NETLINK_INTERFACEy # CONFIG_QUOTA_DEBUG is not set CONFIG_QUOTA_TREEy CONFIG_QUOTACTLy CONFIG_QUOTACTL_COMPATy二、安装 yum install -y quota三、配置 3.1 创建磁盘 格式一定要 …...

解决fidder小黑怪倒出JMeter文件缺失域名、请求头
解决fidder小黑怪倒出JMeter文件缺失域名、请求头 1、目录结构: 2、代码 coding:utf-8 Software:PyCharm Time:2024/7/10 14:02 Author:Dr.zxyimport zipfile import os import xml.etree.ElementTree as ET import re#定义信息头 headers_to_extract [Host, Conn…...

智慧城市的神经网络:Transformer模型在智能城市构建中的应用
智慧城市的神经网络:Transformer模型在智能城市构建中的应用 随着城市化的快速发展,智能城市的概念应运而生,旨在通过先进的信息技术提升城市管理效率和居民生活质量。Transformer模型,作为人工智能领域的一颗新星,其…...

产品经理-研发流程-敏捷开发-迭代-需求评审及产品规划(15)
敏捷开发是以用户的需求进化为核心,采用迭代、循序渐进的方法进行软件开发。 通俗来说,敏捷开发是一个软件开发流程,是一个采用了迭代方法的开发流程 简单来说,迭代就是把一个大产品拆分出一些最小的实现单位。完成不同的迭代就最…...

Ansible 安装及使用说明
方案1. 直接下载 源码包到本地后安装 ansible 下载地址:https://releases.ansible.com/ansible/ ansible社区: https://github.com/ansible/ansible 下载地址:GitHub - ansible/ansible at v2.9.0 方案2. 以腾讯的yum源说明:腾讯云文档…...

MyBatisPlus实现增删改查
文章目录 MyBatisPlus实现增删改查基本操作分页查询配置分页插件 MyBatisPlus实现增删改查 实体类GkUser package com.geekmice.springbootselfexercise.entity;import com.baomidou.mybatisplus.annotation.IdType; import com.baomidou.mybatisplus.annotation.TableField;…...

【Rust】——不安全Rust
💻博主现有专栏: C51单片机(STC89C516),c语言,c,离散数学,算法设计与分析,数据结构,Python,Java基础,MySQL,linux…...

使机器人在执行任务时更加稳定
为了使机器人在执行任务时更加稳定,调整参数时需要考虑多个因素,如步态、速度、角度等。这些参数的调整需要基于实际环境、任务需求和机器人自身的物理特性。以下是一些具体的调整建议: 1. 调整步态和步高 gait_type3; step_height0.03;步态…...
-- libswresample使用说明及函数介绍)
FFmpeg学习(五)-- libswresample使用说明及函数介绍
libswresample Audio合成和重采样 libswresample库用来进行audio数据的合成和重采样操作。调用流程: 调用 swr_alloc 创建SwrContext结构体。设置SwrContext参数,有两种方法: 调用av_opt_set_xx函数逐项设置参数;swr_alloc_set_…...
车载视频监控管理方案:无人驾驶出租车安全出行的保障
近日,无人驾驶出租车“萝卜快跑”在武汉开放载人测试成为热门话题。随着科技的飞速发展,无人驾驶技术已逐渐从概念走向现实,特别是在出租车行业中,无人驾驶出租车的推出将为公众提供更为安全、便捷、高效的出行服务。 视频监控技…...

05STM32EXIT外部中断中断系统
STM32EXIT外部中断&中断系统 中断系统中断触发条件:中断处理流程和用途: STM32中断NVIC嵌套中断向量控制器基本结构NVIC基本结构NVIC优先级分组EXTI简介EXTI基本结构AFIO复用IO口EXTI内部框图旋转编码器简介硬件电路外设手册里的介绍NVIC中断使能寄存…...

MetaGPT和LangGraph对比
MetaGPT和LangGraph是两个不同的AI Agent框架,各有其特点和优势:MetaGPT: MetaGPT是一个多Agent协作框架,模拟软件公司的运作方式。它包含多个角色如产品经理、架构师、项目经理和工程师,每个角色都有特定的职责。MetaGPT采用对话模式&#…...

基于SpringBoot+Hadoop+python的物品租赁系统(带1w+文档)
基于SpringBootHadooppython的物品租赁系统(带1w文档) 基于SpringBootHadooppython的物品租赁系统(带1w文档) 物品租赁系统是电子、信息技术相结合,是一种必然的发展趋势。以互联网为基础,以服务于广大用户为目的,发展整体优势,扩…...

关于 RK3588刷镜像升级镜像”没有发现设备“ 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140287339 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

docker 上传镜像到hub仓库
要将 Docker 镜像上传到 Docker Hub,你需要按照以下步骤操作: 登录 Docker Hub 首先,你需要登录到 Docker Hub。打开终端并运行以下命令:docker login系统会提示你输入 Docker Hub 的用户名和密码。 如果密码忘记可以token登录&a…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...
