对数的基本概念
概念
在数学中,对数是对求幂的逆运算,正如除法是乘法的倒数,反之亦然。这意味着一个数字的对数是必须产生过另一个固定数字(基数)的指数
如果a的x次方等于N(a > 0, 且a不等于1),那么数x叫做以a为底N的对数(logarithm),记做 x=logaN
其中,a叫做对数的底数,N叫做真数

开根号计算

两种特殊的对数
常用对数:将以10为底的对数叫常用对数,并把log10N 记作lgN
自然对数:在科学技术中常使用以无理数 e = 2.71828… 为底数的对数,以e为底的对数称为自然对数,并且把logeN 记做 lnN
对数与指数的关系
当 a > 0, 且 a != 1 时, a ^ x = N < = > logaN
对数恒等式 : a ^ logaN = N(a > 0, 且 a != 1, N > 0)
定义
特别地,我们称以10为底的对数叫做常用对数(common logarithm),并记为lg
称以无理数e(e=2.71828…)为底的对数称为自然对数(natural logarithm),并记为ln
零没有对数
在实数范围内,负数无对数。 [3] 在虚数范围内,负数是有对数的
对数的运算性质
a > 0 , a != 1, M > 0, N > 0

相关文章:

对数的基本概念
概念 在数学中,对数是对求幂的逆运算,正如除法是乘法的倒数,反之亦然。这意味着一个数字的对数是必须产生过另一个固定数字(基数)的指数 如果a的x次方等于N(a > 0, 且a不等于1),那么数x叫做以a为底N的…...

C双指针滑动窗口算法
这也许是双指针技巧的最⾼境界了,如果掌握了此算法,可以解决⼀⼤类⼦字符串匹配的问题 原理 1、我们在字符串 S 中使⽤双指针中的左右指针技巧,初始化 left right 0,把索引闭区间 [left, right] 称为⼀个「窗⼝」。 2、我们先…...
WPF学习(6) -- WPF命令和通知
一 、WPF命令 1.ICommand代码 创建一个文件夹和文件 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Input;namespace 学习.Command {public class MyCommand : ICommand{Acti…...

升级到LVGL9的一些变化(后续发现再补充)
目录 一、主要内容 二、新增内容 三、常规API变化 四、Display API(显示API) 五、其他 最近在将LVGL8的demo代码升级到LVGL9,带来不小的变化 ,收集网上的一些内容,整理如下: 一、主要内容 二、新增内容 三、常规API变化 四、Display API(显示API)...

当在多线程环境中使用 C++进行编程时,怎样确保线程安全以及如何处理线程之间的同步和通信?
在C中确保线程安全性和处理线程之间的同步和通信有多种方法。下面是一些常用的技术和技巧: 互斥锁:使用互斥锁可以确保只有一个线程可以访问共享资源。在访问共享资源之前获取锁,在完成后释放锁。这可以防止多个线程同时访问同一份数据&#…...

博物馆地图导航系统:高精度地图引擎与AR/VR融合,实现博物馆数字化转型
在人民日益追求精神文化的时代下,博物馆作为传承与展示人类文明的璀璨殿堂,其重要性不言而喻。然而,随着博物馆规模的不断扩大和藏品种类的日益丰富,游客在享受知识盛宴的同时,也面临着“迷路”与“错过”的困扰。博物…...

liunx作业笔记1
一、选择题(每小题2分,共20分) 1、下列变量命名为Shell中无效变量名的是( D ) A、v_ar1 B、var1 C、_var D、*var 变量名以字母开头,包含下划线和数字。 2、关于expr命令的使用下列命令中得数不等于…...

大话C语言:第31篇 指针和数组的关系
数组在内存中是连续存放的,其名称代表了数组首元素的首地址,该地址是常量, 也就是一个指向数组首元素的指针。因此,指针和数组有着密切的关系: 可以使用指针来访问和操作数组中的元素。通过指针的算术运算,…...

Mysql-索引应用
目录 索引应用 MySQL有哪些索引? 普通索引和唯一索引有什么区别? 哪个更新性能更好? 、 聚簇索引的主键索引怎么设置? 追问:假如你不设置会怎么样? 我们一般选择什么样的字段来建立索引? 索引越多越好吗? 索引怎么优化? (覆盖索引优化、防止索引失效、…...

Facebook 开源计算机视觉 (CV) 和 增强现实 (AR) 框架 Ocean
Ocean 是一个独立于平台的框架,支持所有主要操作系统,包括 iOS、Android、Quest、macOS、Windows 和 Linux。它旨在彻底改变计算机视觉和混合现实应用程序的开发。 Ocean 主要使用 C 编写,包括计算机视觉、几何、媒体处理、网络和渲染&#x…...

【接口自动化_13课_接口自动化总结】
一、自我介绍 二、项目介绍 自己的职责、项目流程 1)功能测试,怎么设计用例的--测试策略 2)功能测试为什么还有代码实现,能用工具实现,为什么还用代码实现。 基本情况 项目名称:项目类型:项目测试人员…...
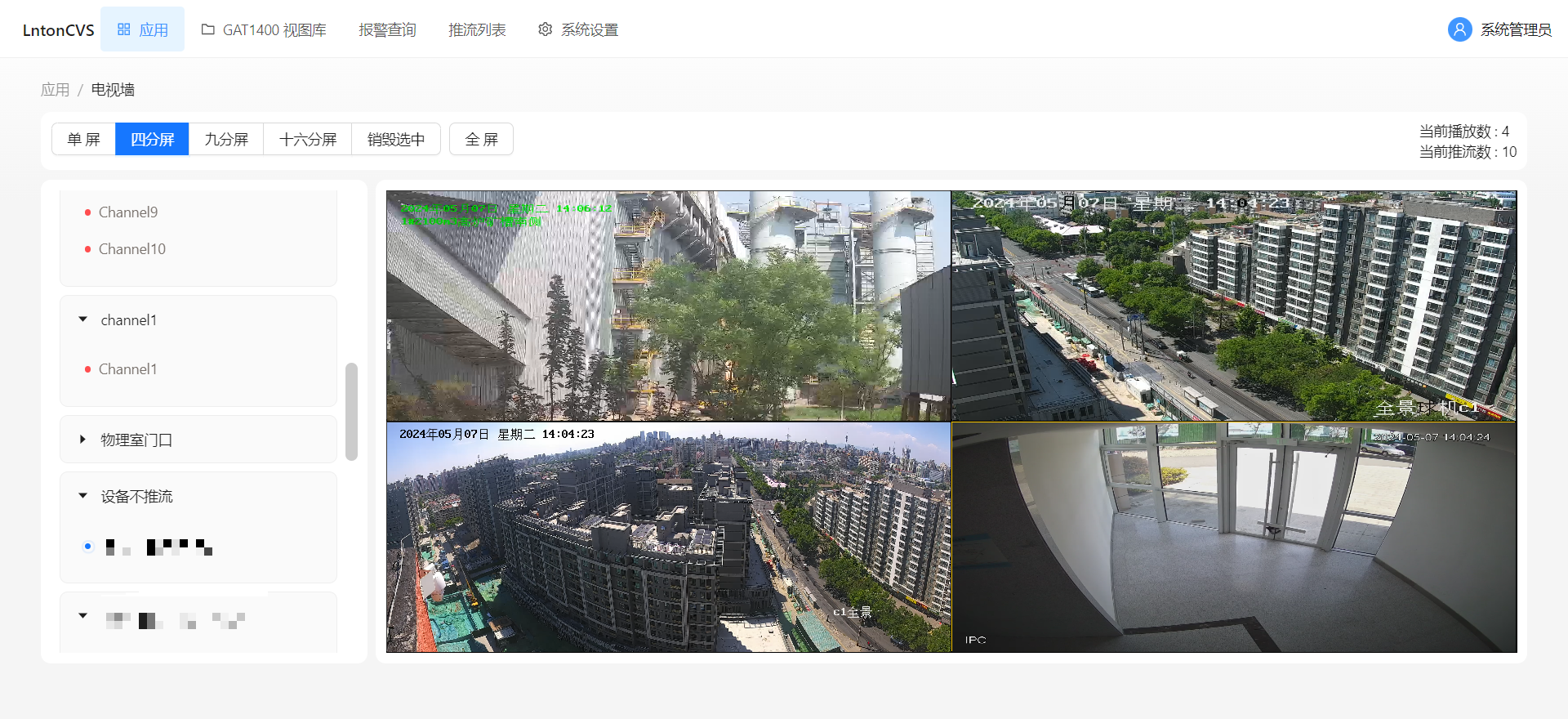
安防管理平台LntonCVS视频汇聚融合云平台智慧火电厂安全生产管理应用方案
中国的电力产业作为国民经济发展的重要能源支柱,被视为国民经济的基础产业之一。目前,我国主要依赖火力发电,主要燃料包括煤炭、石油和天然气等,通过燃烧转化为动能,再转变为电能输送至全国各地。火力发电量占全国发电…...

【Web性能优化】在Vue项目中使用defer优化白屏,秒加载!
历史小剧场 相对而言,流芳千古的钱谦益先生,就有点儿区别了,除了家产外,也很能挣钱(怎么来的就别说了),经常出没红灯区,六十岁多了,还娶了柳如是,明朝亡时&am…...

springboot上传图片
前端的name的值必须要和后端的MultipartFile 形参名一致 存储本地...

python入门:python及PyCharm安装
前言 我们将详细介绍如何在系统上安装Python及使用PyCharm创建项目的具体流程。Python是一种广泛应用的编程语言,其简单易学的特点使其成为初学者的首选。而PyCharm则是一个功能强大的Python IDE,可以极大地提高开发效率。通过本文,你将学会…...

链接追踪系列-04.linux服务器docker安装elk
[rootVM-24-17-centos ~]# cat /proc/sys/vm/max_map_count 65530 [rootVM-24-17-centos ~]# sysctl -w vm.max_map_count262144 vm.max_map_count 262144 #先创建出相应目录:/opt/dockerV/es/…docker run -e ES_JAVA_OPTS"-Xms512m -Xmx512m" -d -p 92…...

深入探讨微服务架构设计模式与常见实践
深入探讨微服务架构设计模式与常见实践 引言 在现代软件开发中,微服务架构因其灵活性和可扩展性被广泛采用。本文将深入探讨微服务架构的设计理念和常见模式,详细介绍每个模式的实现方法,并分别提供适用于Ubuntu和CentOS的具体命令和代码示…...

【java】合并数组的两种方法
文章目录 1.利用arraycope的方法2.将两数组合并 ,在排序 1.利用arraycope的方法 public class MergeArr {public static void main(String[] args) {int[] arr1 {1,2,3,4,5,6};int[] arr2 {7,8,9};//合并完的数组int[] arr3 new int[arr1.length arr2.length];…...

[图解]分析模式-01-概述1
1 00:00:01,380 --> 00:00:01,770 好 2 00:00:02,340 --> 00:00:06,440 非常感谢大家能够来上我们 3 00:00:06,450 --> 00:00:07,960 分析模式高阶的课程 4 00:00:09,310 --> 00:00:13,440 这个内容之前在分析设计高阶 5 00:00:13,450 --> 00:00:17,840 也就…...

【网络安全】Oracle:SSRF获取元数据
未经许可,不得转载。 文章目录 前言正文漏洞利用 前言 Acme 是一家广受欢迎的播客托管公司,拥有庞大的客户群体。与许多大型运营公司一样,Acme 采用了Apiary的服务,使用户能够安全高效地管理他们的播客。 Apiary 于2017年初被Or…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
