【人工智能】-- 受限玻尔兹曼机

个人主页:欢迎来到 Papicatch的博客
课设专栏 :学生成绩管理系统
专业知识专栏: 专业知识

文章目录
🍉引言
🍉受限玻尔兹曼机
🍈RBM的结构
🍍RBM的架构图
🍍RBM的经典实现
🍍代码实现
🍍代码分析
🍉总结
🍉引言
在当今科技飞速发展的时代,人工智能的研究不断取得突破性的进展。其中,受限玻尔兹曼机作为一种重要的模型,正逐渐引起人们的广泛关注。它独特的结构和强大的学习能力,为解决各种复杂的问题提供了新的思路和方法。受限玻尔兹曼机不仅在理论研究上具有深刻的意义,在实际应用中也展现出了巨大的潜力,例如图像识别、语音处理、自然语言处理等领域。
🍉受限玻尔兹曼机
受限玻尔兹曼机(Restricted Boltzmann Machine,RBM)是一种生成性随机人工神经网络,也是一种无向概率图模型,并且受限为二分图。
整个模型有两层,即可见层(包含可见单元)和隐藏层(包含隐单元),满足层内无连接,层间全连接。这种限制使得它在神经元之间的连接上有特定的规则,来自两组单元中的每一组的一对节点(通常称为“可见”和“隐藏”单元)可以在它们之间具有对称连接,而组内的节点之间没有连接。相比一般的玻尔兹曼机,这种限制允许使用更有效的训练算法。
RBM 通常由二值隐单元和可见单元组成,其中权重矩阵 中的每个元素指定了隐单元
和可见层单元
之间边的权重。
此外,对于每个可见层单元 有偏置项
,对每个隐层单元
有偏置项
。具体来说,需满足以下条件

其能量函数对于一组给定的状态 定义为:

由能量函数可以给出状态 的联合概率分布:

其中, 是归一化常数,计算式为
,其计算复杂度为
。可见层的边缘分布:
;隐藏层的边缘分布:
。
RBM 的一个重要性质是,由于它是一个二分图,层内没有边相连,因而隐藏层的激活状态在给定可见层节点取值的情况下是条件独立的,类似地,可见层节点的激活状态在给定隐藏层节点取值的情况下也条件独立,用数学公式表示为:

由此可以推导得出在给定可视层 的基础上,隐层第
个节点为 1 或者为 0 的概率为:

在给定隐层 的基础上,可视层第
个节点为 1 或者为 0 的概率为:

在训练 RBM 时,关键是计算模型中的参数 。通常采用对数损失函数,并考虑最大化对数似然函数。但直接按梯度公式计算梯度的复杂度很高,因为其中涉及到归一化常数
的计算,而
的计算复杂度为
。
为解决这个问题,一般使用基于马尔可夫链蒙特卡罗(MCMC)的方法来模拟计算梯度,如 Geoffrey Hinton 提出的对比散度(contrastive divergence,CD)算法。该算法给定样本 后,取初始值
,然后执行
步 Gibbs 采样,先后采样得到
和
。Gibbs 采样得到的样本服从联合分布
,利用采样得到的
可以估算梯度公式中期望项的近似值,从而得到梯度的近似值,之后在每一步利用梯度上升法进行参数更新。
RBM 可用于降维、分类、协同过滤、特征学习、生成模型等任务。根据任务的不同,它可以使用监督学习或无监督学习的方法进行训练。例如在推荐系统中,可以把每个用户对各个物品的评分作为可见层神经元的输入,从而进行训练。
RBM 在深度学习中有重要应用,它可以通过“堆叠”形成深层信念网络等更复杂的结构。但 RBM 也存在一些局限性,例如在处理大规模数据时可能效率不高,对初始值敏感等。不过,研究人员仍在不断探索和改进 RBM 及其相关算法,以拓展其应用领域和提高性能。
🍈RBM的结构
🍍RBM的架构图

🍍RBM的经典实现

🍍代码实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split# 加载 MNIST 数据集
mnist = fetch_openml('mnist_784', version=1, cache=True)
X = mnist.data
y = mnist.target# 数据预处理
X = preprocessing.MinMaxScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)class RBM:def __init__(self, n_visible, n_hidden, learning_rate=0.1, n_epochs=100):"""初始化 RBM 模型参数:n_visible:可见层神经元数量(输入数据的维度)n_hidden:隐藏层神经元数量learning_rate:学习率n_epochs:训练轮数"""self.n_visible = n_visibleself.n_hidden = n_hiddenself.learning_rate = learning_rateself.n_epochs = n_epochs# 随机初始化权重矩阵 W,偏置向量 bv(可见层)和 bh(隐藏层)self.W = np.random.randn(n_visible, n_hidden) * 0.1self.bv = np.zeros(n_visible)self.bh = np.zeros(n_hidden)def sigmoid(self, x):"""Sigmoid 激活函数参数:x:输入值返回:Sigmoid 函数的输出"""return 1 / (1 + np.exp(-x))def sample_hidden(self, v):"""根据给定的可见层状态 v 采样隐藏层参数:v:可见层状态返回:隐藏层的激活概率 p_hidden 和采样后的隐藏层状态 h"""hidden_activation = np.dot(v, self.W) + self.bhp_hidden = self.sigmoid(hidden_activation)return p_hidden, np.random.binomial(1, p_hidden)def sample_visible(self, h):"""根据给定的隐藏层状态 h 采样可见层参数:h:隐藏层状态返回:可见层的激活概率 p_visible 和采样后的可见层状态 v_prime"""visible_activation = np.dot(h, self.W.T) + self.bvp_visible = self.sigmoid(visible_activation)return p_visible, np.random.binomial(1, p_visible)def train(self, X):"""训练 RBM 模型参数:X:训练数据"""for epoch in range(self.n_epochs):for v in X:# 正向传播:根据输入的可见层状态 v 计算隐藏层的激活概率和采样后的隐藏层状态p_hidden, h = self.sample_hidden(v)# 反向传播:根据采样得到的隐藏层状态 h 计算可见层的激活概率和采样后的可见层状态 v_primep_visible, v_prime = self.sample_visible(h)# 更新参数# 计算权重更新量 dWdW = np.outer(v, p_hidden) - np.outer(v_prime, p_hidden)# 更新权重 Wself.W += self.learning_rate * dW# 更新可见层偏置 bvself.bv += self.learning_rate * (v - v_prime)# 更新隐藏层偏置 bhself.bh += self.learning_rate * (p_hidden - np.mean(p_hidden))def reconstruct(self, X):"""对输入数据进行重建参数:X:输入数据返回:重建后的可见层状态"""h = np.zeros((X.shape[0], self.n_hidden))for i, v in enumerate(X):_, h[i] = self.sample_hidden(v)_, v_prime = self.sample_visible(h)return v_prime# 初始化 RBM 模型,设置可见层神经元数量为 784(MNIST 图像的维度),隐藏层神经元数量为 128
rbm = RBM(n_visible=784, n_hidden=128, learning_rate=0.1, n_epochs=50)# 训练模型
rbm.train(X_train)# 重建测试集图像
reconstructed_images = rbm.reconstruct(X_test)# 展示原始图像和重建图像
n_images = 5
for i in range(n_images):original_image = X_test[i].reshape(28, 28)reconstructed_image = reconstructed_images[i].reshape(28, 28)plt.subplot(2, n_images, i + 1)plt.imshow(original_image, cmap='gray')plt.axis('off')plt.subplot(2, n_images, i + 1 + n_images)plt.imshow(reconstructed_image, cmap='gray')plt.axis('off')plt.show()🍍代码分析
RBM 类的 __init__ 方法:
- 初始化模型的参数,包括可见层和隐藏层的神经元数量、学习率和训练轮数。
- 随机初始化权重矩阵
W、可见层偏置bv和隐藏层偏置bh。
sigmoid 方法:定义了 Sigmoid 激活函数,用于计算神经元的激活概率。
sample_hidden 方法:
- 计算给定可见层状态下隐藏层的激活值。
- 通过激活值计算隐藏层的激活概率。
- 基于激活概率进行二项分布采样得到隐藏层的状态。
sample_visible 方法:与 sample_hidden 类似,用于根据隐藏层状态采样可见层状态。
train 方法:
- 在每一轮训练中,遍历训练数据中的每个样本。
- 进行正向传播,从可见层到隐藏层的采样。
- 进行反向传播,从隐藏层到可见层的采样。
- 根据采样结果计算权重和偏置的更新量,并进行更新。
reconstruct 方法:
- 首先对输入数据采样得到隐藏层状态。
- 然后根据隐藏层状态采样重建可见层状态。
在主程序中:
- 加载 MNIST 数据集并进行预处理和划分。
- 初始化 RBM 模型并进行训练。
- 对测试集数据进行重建,并展示原始图像和重建图像的对比。
这段代码主要实现了一个受限玻尔兹曼机(RBM)模型,并将其应用于 MNIST 数据集的图像重建任务。
首先,代码从开放数据集中加载 MNIST 数据,进行预处理和划分。然后定义了 RBM 类,在类的初始化方法中,设定了模型的关键参数,包括可见层和隐藏层的神经元数量、学习率以及训练轮数,并随机初始化了权重和偏置。
RBM 类中包含了 sigmoid 激活函数,以及用于正向和反向传播的 sample_hidden 和 sample_visible 方法。训练方法 train 通过不断的正向和反向传播,并基于采样结果更新权重和偏置来优化模型。reconstruct 方法用于对输入数据进行重建。
在主程序中,初始化并训练 RBM 模型,最后对测试集数据进行重建,并通过图像展示原始图像和重建图像的对比,以直观评估模型的重建效果。
🍉总结
受限玻尔兹曼机(RBM)是一种具有独特结构和强大学习能力的概率图模型。
在结构上,RBM 由两层神经元组成,即可见层和隐藏层。层内神经元无连接,层间神经元全连接。这种结构简化了计算,同时也使得模型能够有效地学习数据中的特征和模式。
在学习过程中,RBM 通过不断调整参数(包括权重、可见层偏置和隐藏层偏置)来优化模型。常见的学习算法如对比散度(CD)算法,通过采样和近似计算梯度来更新参数。
RBM 具有多种应用,例如在数据降维方面,它能够将高维数据映射到低维的隐藏层表示;在特征学习中,能够自动从原始数据中提取有意义的特征;在生成模型中,可以生成新的数据样本。
然而,RBM 也存在一些局限性。例如,训练时间可能较长,尤其是在处理大规模数据时;对初始参数的设置较为敏感;模型的解释性相对较复杂等。
尽管如此,RBM 在深度学习领域仍然具有重要地位,其思想和方法为后续更复杂的深度模型的发展提供了基础和启发。

相关文章:

【人工智能】-- 受限玻尔兹曼机
个人主页:欢迎来到 Papicatch的博客 课设专栏 :学生成绩管理系统 专业知识专栏: 专业知识 文章目录 🍉引言 🍉受限玻尔兹曼机 🍈RBM的结构 🍍RBM的架构图 🍍RBM的经典实现 &…...

在 Android 中定义和使用自定义属性
1. 定义自定义属性 首先,我们需要在 res/values/attrs.xml 文件中定义自定义属性。这些属性可以是颜色、尺寸、字符串等。 创建或打开 res/values/attrs.xml 文件,并添加以下内容: <?xml version"1.0" encoding"utf-8&…...

【实战:python-Django发送邮件-短信-钉钉通知】
一 Python发送邮件 1.1 使用SMTP模块发送邮件 import smtplib from email.mime.text import MIMEText from email.header import Headermsg_from 306334678qq.com # 发送方邮箱 passwd luzdikipwhjjbibf # 填入发送方邮箱的授权码(填入自己的授权码,相当于邮箱…...

Todo List
待整理的笔记,先列出来,防止后面忘记要整理什么内容。一个一个整理: Linux内核ARM架构(v8)的系统调用的实现过程;open()/write()/read()在Linux内核中的详细实现过程,到驱动中注册的操作集的调用过程;文件…...

【Redis】Redis十大类型
文章目录 前言一、string字符串类型二、List列表类型三、 Hash表四、 Set集合五、 ZSet有序集合六、 GEO地理空间七、 HyperLogLog基数统计八、Bitmap位图九、bitfield位域十、 Stream流10.1 队列指令10.2 消费组指令10.3 ACK机制 前言 redis是k-v键值对进行存储,k…...
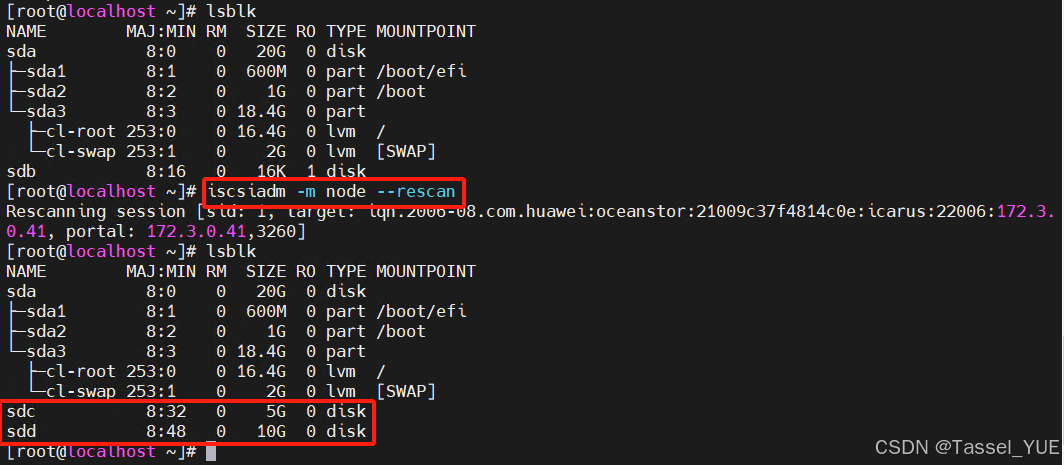
存储实验:Linux挂载iscsi硬盘与华为OceanStor创建LUN全流程
目录 目的环境规划实验实验流程Centos配置0. 关闭防火墙1. 设置网卡信息2. 配置路由3. iscsiadm连接存储 iSCSI LUN创建(以华为OceanStor为例)验证1. 验证是否成功2. 开启自动挂载 目的 实现Linux连接iscsi硬盘,同时实现开机自启挂载 环境规…...

高可用系统架构设计技术方案:Java架构师视角
在现代互联网环境下,高可用性(High Availability, HA)已成为衡量系统质量的重要指标之一。对于Java架构师而言,设计一套能够保证业务连续性、快速恢复和持续服务的高可用系统架构,是一项复杂而挑战性的任务。本文将从J…...
)
C++ --> 类和对象(三)
欢迎来到我的Blog,点击关注哦💕 前言 前面已经对类和对象有一定的了解,接下来再次深入的了解一下。 一、深入理解构造函数 构造函数体赋值: 虽然上述构造函数调用之后,对象中已经有了一个初始值,但是不能…...
)
JS【详解】类 class ( ES6 新增语法 )
本质上,类只是一种特殊的函数。 console.log(typeof 某类); //"function"声明类 class 方式 1 – 类声明 class Car {constructor(model, year) {this.model model;this.year year;} }方式 2 – 类表达式 匿名式 const Car class {constructor(mod…...

vue中使用$set方法给对象添加属性
vue中可以使用$set()给对象添加属性,但不是所有的对象都可以使用,vue中api明确说明,它必须用于向响应式对象上添加属性 响应式对象,vue的响应式原理,可以查看:深入响应式原理 — Vue.js ①对象赋值 this…...

【Python】ftplib的使用
仅描述基础要点,备忘。 python自带ftplib库,可实现ftp读写。 1 要点 ftp未使用默认端口21时,需显示指定端口。ftp路径带有中文,可能需要设置ftp的encoding属性为 gbk。ftplib不支持递归创建目录,需手动创建层级目录…...
)
CSS 【详解】CSS 函数(含 calc,min,max,clamp,cubic-bezier,env,steps 等)
函数描述CSS 版本attr()返回选择元素的属性值。2calc()允许计算 CSS 的属性值,比如动态计算长度值。3cubic-bezier()定义了一个贝塞尔曲线(Cubic Bezier)。3hsl()使用色相、饱和度、亮度来定义颜色。3hsla()使用色相、饱和度、亮度、透明度来定义颜色。3linear-grad…...
)
简单理解Lua 协程(coroutine)
也许更好的阅读体验 协程简单理解为可以暂停的线程,但是同一时刻只有一个协程可以处于运行状态。 文章目录 coroutine.create()coroutine.resume()coroutine.wrap()coroutine.yield()coroutine.resume()参数传递resume和yield之间互换数据 coroutine.create() lua…...

(day18) leetcode 204.计数质数
描述 给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。 示例 1: 输入:n 10 输出:4 解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。示例 2: 输入:n 0 输出:0示例 3…...

SadTalker数字人服务器部署
一、单独SadTalker部署 git clone https://github.com/OpenTalker/SadTalker.gitcd SadTalker conda create -n sadtalker python3.8conda activate sadtalkerpip install torch1.12.1cu113 torchvision0.13.1cu113 torchaudio0.12.1 --extra-index-url https://download.pyto…...

Python实现一对多WebSocket发送给指定多个客户端
在一对多的WebSocket场景下,如果你想要向特定的多个客户端发送消息,而不是广播给所有客户端,你需要维护一个能够标识每个客户端的方式,比如使用用户名或者客户端ID。这样,你就可以根据需要选择向哪些客户端发送消息。 …...

Power BI 工具介绍
Power BI是一款商业智能(BI)软件,由微软开发,旨在帮助用户将复杂的数据转化为视觉化的交互式见解。Power BI提供了一套完整的工具,包括数据连接、数据准备、数据建模、数据分析和数据可视化等功能,使用户能…...

银河麒麟高级服务器操作系统V10加固操作指南
1:检查系统openssh安全配置: 2:检查是否设置口令过期前警告天数: 3:检查账户认证失败次数限制: 修改/etc/pam.d/system-auth文件中deny的参数即可 4:检查是否配置SSH方式账户认证失败次数限制:...

(leetcode学习)15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例 1&a…...

算法训练 | 图论Part8 | 117. 软件构建、47. 参加科学大会
目录 117. 软件构建 拓扑排序法 47. 参加科学大会 dijkstra法 117. 软件构建 题目链接:117. 软件构建 文章讲解:代码随想录 拓扑排序法 代码一:拓扑排序 #include <iostream> #include <vector> #include <queue> …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
