【Java--数据结构】二叉树oj题(上)
前言
欢迎关注个人主页:逸狼
创造不易,可以点点赞吗~
如有错误,欢迎指出~
判断是否是相同的树
oj链接
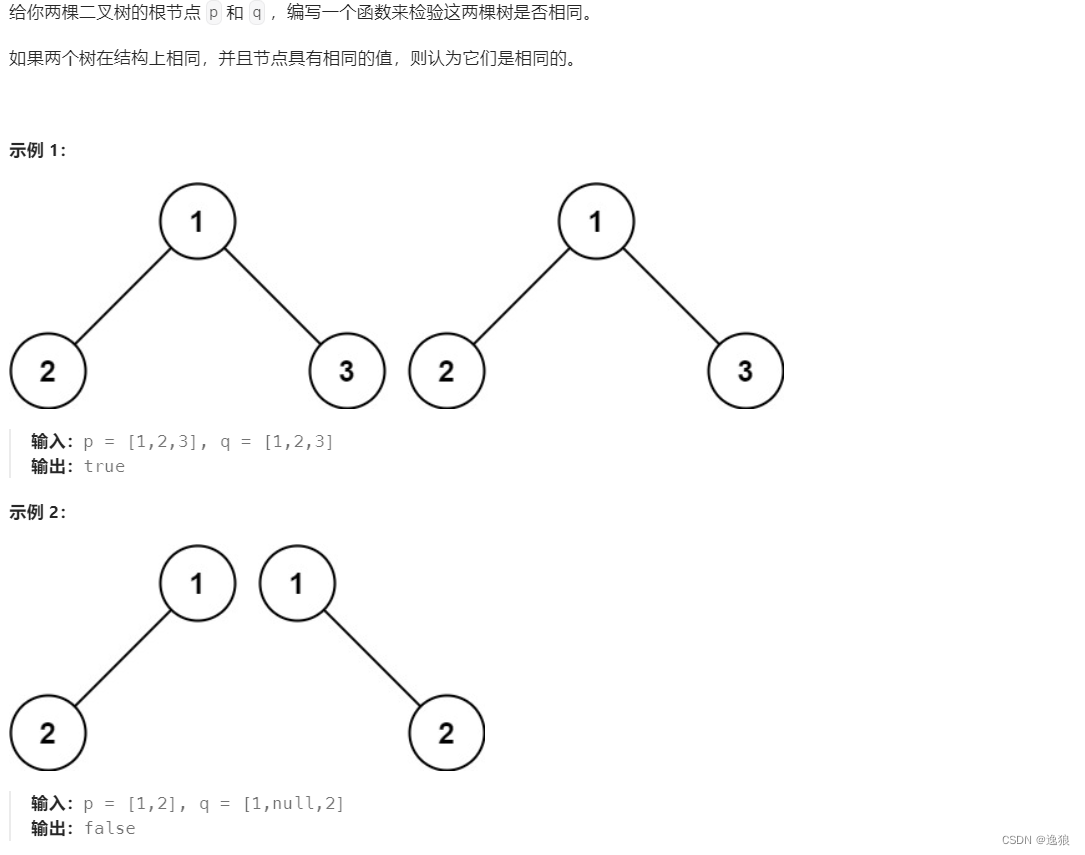
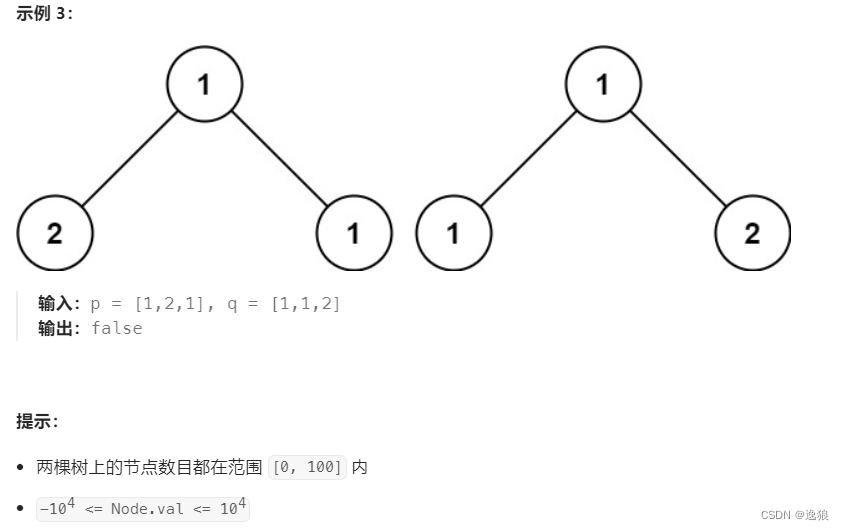
要判断树是否一样,要满足3个条件
- 根的 结构 和 值 一样
- 左子树的结构和值一样
- 右子树的结构和值一样
所以就可以总结以下思路:
- 一个为空,一个不为空--》一定不相同
- 两个都为空--》 相同
- 都不为空 ,但值不一样--》一定不相同
- 最后递归判断 左子树和右子树都要相同--》两棵树相同
其中该题的时间复杂度为O(min(m,n)),也就是取m和n中最小值(假设p的节点数为m个,q的节点数为n个)
public boolean isSameTree(TreeNode p, TreeNode q) {//一个为空,一个不为空if(p!=null&&q==null||p==null&&q!=null){return false;}//此时要么两个都为空,要么都不为空if(p==null&&q==null){return true;}//都不为空if(p.val!=q.val){return false;}//此时两个都不为空,val值也一样,说明根节点相同//判断左右树是否相同return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
另一棵树的子树
oj链接
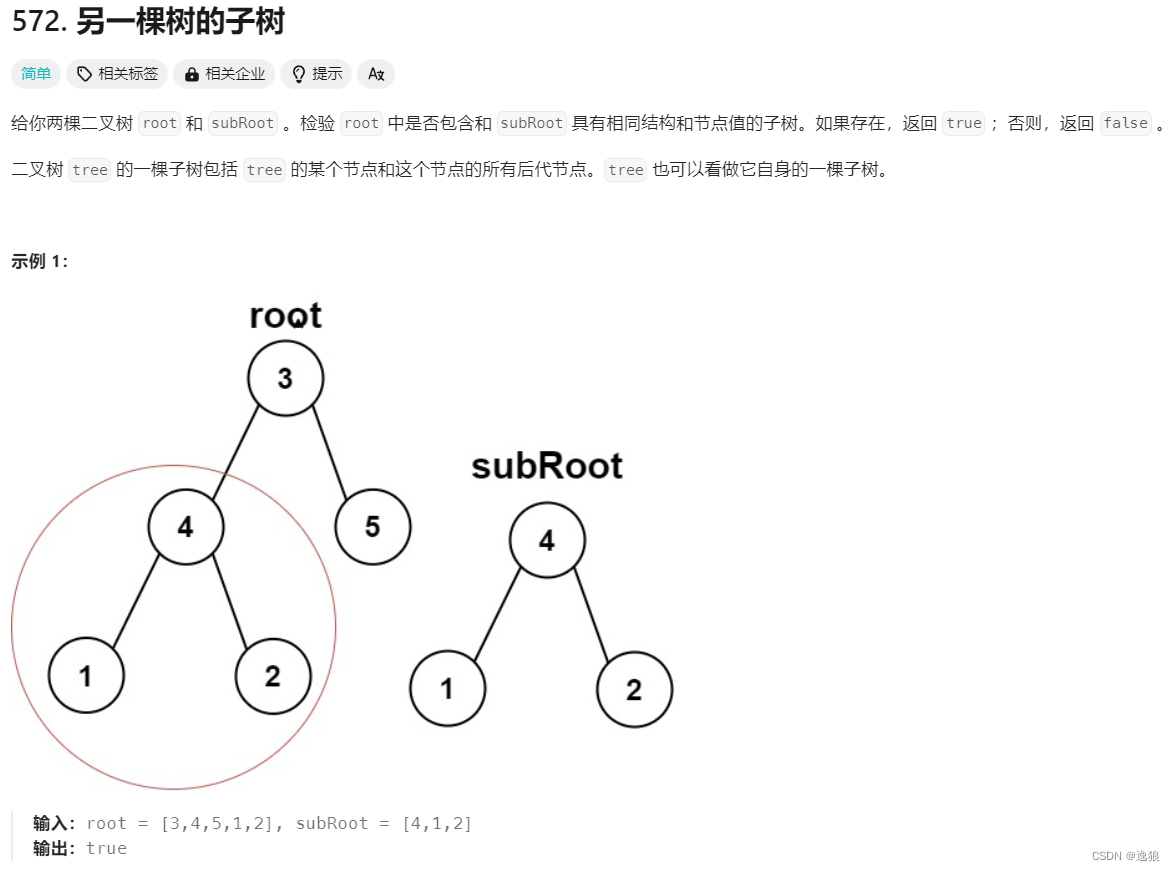
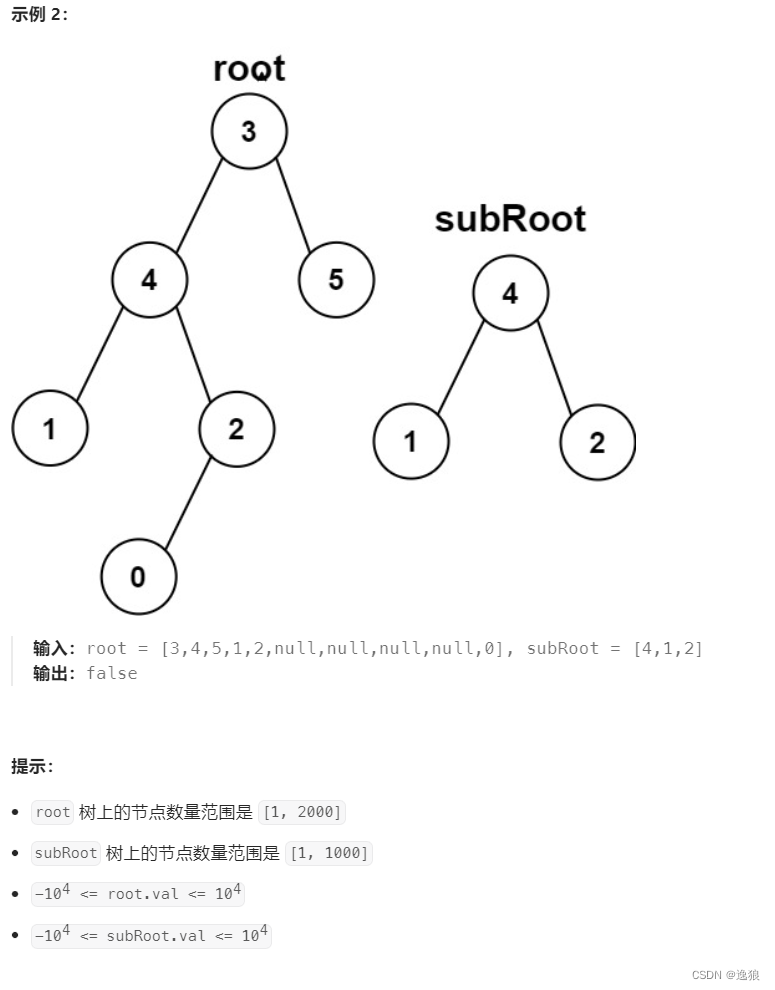
当两颗树相同时,也属于子树
所以步骤如下
- 判断是不是两颗相同的树
- 若不是,有可能是左子树的子树
- 也有可能是右子树的子树
其中该题的时间复杂度为m*n (假设root有n个节点,subRoot有m个节点),原因是root的每一个节点都要和subRoot的节点比对
public boolean isSubtree(TreeNode root, TreeNode subRoot) {//因为root要递归,递归到后面root可能为空if(root==null){return false;}//两颗树相同时,成立if(isSameTree(root,subRoot)){return true;}//判断root的左子树和subRootif(isSubtree(root.left,subRoot)){return true;}//判断root的右子树和subRootif(isSubtree(root.right,subRoot)){return true;}return false;}public boolean isSameTree(TreeNode p, TreeNode q) {//一个为空,一个不为空if(p!=null&&q==null||p==null&&q!=null){return false;}//此时要么两个都为空,要么都不为空if(p==null&&q==null){return true;}//都不为空if(p.val!=q.val){return false;}//此时两个都不为空,val值也一样,说明根节点相同//判断左右树是否相同return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);}翻转二叉树
oj链接
让root的左节点和右节点交换,再递归遍历root.left和root.right使左子树和右子树都翻转。
代码优化:若只有一个根节点(左右子树都为空),直接返回;减少了递归和交换的次数
public TreeNode invertTree(TreeNode root) {if(root==null){return null;}//代码优化部分******减少一些递归和交换的次数if(root.left==null&&root.right==null){return root;}// ******TreeNode ret=root.left;root.left=root.right;root.right=ret;invertTree(root.left);invertTree(root.right);return root;}判断一颗二叉树是否是平衡二叉树
平衡二叉树 是指该树所有节点的左右子树的深度相差不超过 1
oj链接
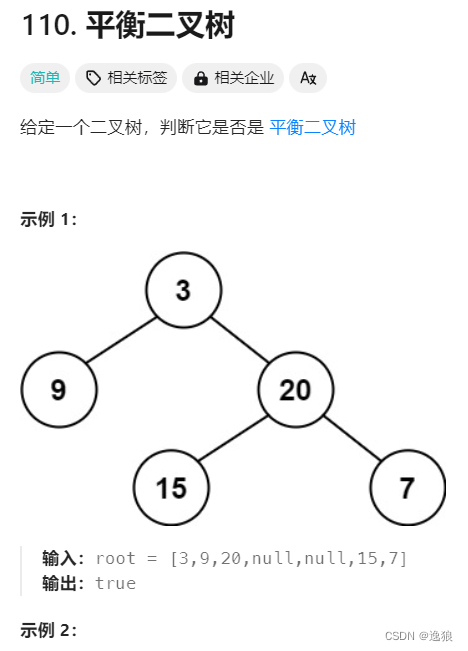
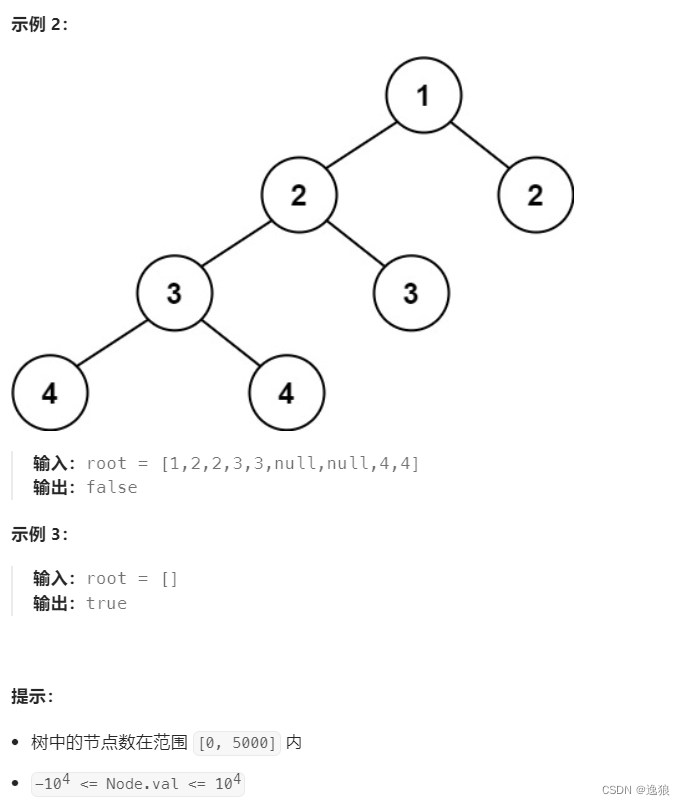
判断步骤:
当前root的 左子树 和 右子树的高度差<=1
同时满足root的左 右子树平衡
其中该题的时间复杂度为O(n^2)
public boolean isBalanced(TreeNode root) {if(root==null) return true;int leftH=maxDepth(root.left);int rightH=maxDepth(root.right);return Math.abs(leftH-rightH)<=1&&isBalanced(root.left)&&isBalanced(root.right);}public int maxDepth(TreeNode root){if(root==null){return 0;}int leftH=maxDepth(root.left);int rightH=maxDepth(root.right);return leftH>rightH?leftH+1:rightH+1;}代码优化,使得时间复杂度变为O(n)
public boolean isBalanced(TreeNode root) {if(root==null) return true;return maxDepth(root)>=1;}public int maxDepth(TreeNode root){if(root==null){return 0;}int leftH=maxDepth(root.left);if(leftH<0){return -1;}int rightH=maxDepth(root.right);if(rightH<0){return -1;}if(Math.abs(leftH-rightH)<=1){return leftH>rightH?leftH+1:rightH+1;}else{return -1;}}第三种写法
public boolean isBalanced(TreeNode root) {if(root==null) return true;return maxDepth(root)>=1;}public int maxDepth(TreeNode root){if(root==null){return 0;}int leftH=maxDepth(root.left);// if(leftH<0){// return -1; // }int rightH=maxDepth(root.right);// if(rightH<0){// return -1;// }if(leftH>=0&&rightH>=0&&Math.abs(leftH-rightH)<=1){return Math.max(leftH,rightH)+ 1;}else{return -1;}}相关文章:

【Java--数据结构】二叉树oj题(上)
前言 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 判断是否是相同的树 oj链接 要判断树是否一样,要满足3个条件 根的 结构 和 值 一样左子树的结构和值一样右子树的结构和值一样 所以就可以总结以下思路…...

微服务之间Feign调用
需使用的服务 FeignClient(name "rdss-back-service", fallback SysUserServiceFallback.class, configuration FeignConfiguration.class) public interface SysUserService {/*** 订单下单用户模糊查询*/GetMapping(value "/user/getOrderUserName")…...
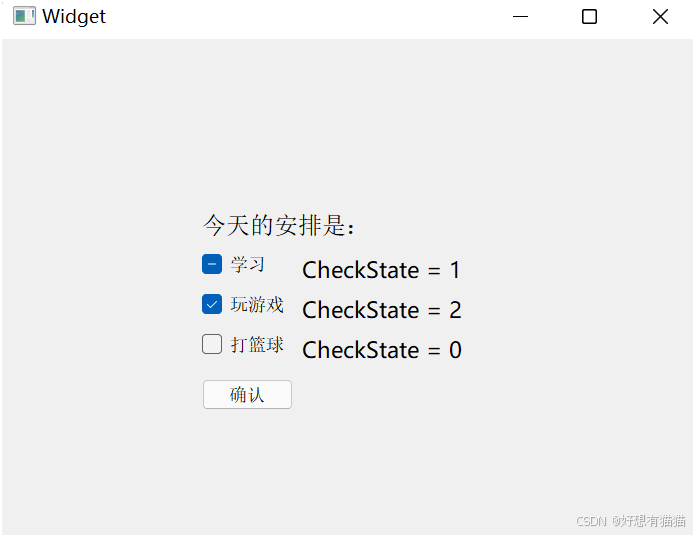
【Qt】按钮的属性相关API
目录 一. QPushButton 二. QRadioButton 按钮组 三. QCheckBox Qt中按钮的继承体系如下图 QAbstractButton是一个抽象类,集成了按钮的核心属性和API 按钮说明QPushButton(普通按钮)最常见的按钮,用于触发操作或者事件。可以设…...

blender和3dmax和maya和c4d比较
Blender、3ds Max、Maya和Cinema 4D (C4D)都是强大的3D建模和动画软件,但它们各有特点和适用领域。以下是它们的比较: Blender: 开源免费全面的功能,包括建模、动画、渲染、视频编辑等学习曲线较陡峭,但社区支持强大适合独立艺术家…...

visio保存一部分图/emf图片打开很模糊/emf插入到word或ppt中很模糊
本文主要解决三个问题 visio保存一部分图 需求描述:在一个visio文件中画了很多个图,但我只想把其中一部分保存成某种图片格式,比如jpg emf png之类的,以便做后续的处理。 方法:超级容易。 选中希望保存的这部分图&…...
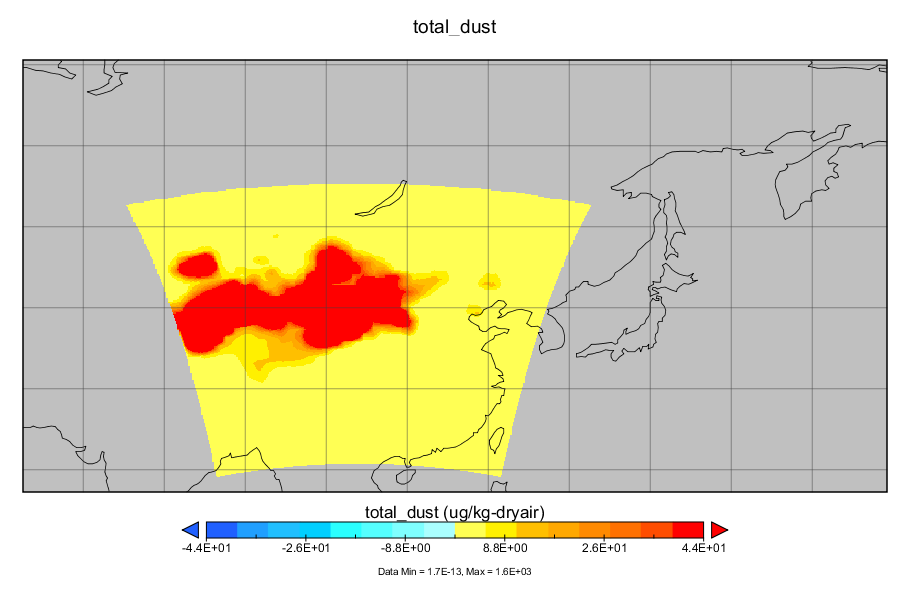
沙尘传输模拟教程(基于wrf-chem)
沙尘传输模拟教程(基于wrf-chem) 文章目录 沙尘传输模拟教程(基于wrf-chem)简介实验目的wrf-chem简介 软件准备wps、wrf-chem安装conda安装ncl安装ncap安装 数据准备气象数据准备下垫面数据准备 WPS数据预处理namelist.wps的设置geogrid.exe下垫面处理ungrib.exe气象数据预处理…...
纯净测试)
使用 Python 进行测试(8)纯净测试
原文:Testing with Python (part 8): purity test 总结 如果你要使用综合测试(integrated tests): def test_add_new_item_to_cart(product, cart):new_product Product.objects.create(nameNew Product, price15.00)new_cart…...
python的tkinter、socket库开发tcp的客户端和服务端
一、tcp通讯流程和开发步骤 1、tcp客户端和服务端通讯流程图 套接字是通讯的利器,连接时要经过三次握手建立连接,断开连接要经过四次挥手断开连接。 2、客户端开发流程 1)创建客户端套接字 2)和服务端器端套接字建立连接 3&#x…...

Python面试题:Python中的异步编程:详细讲解asyncio库的使用
Python 的异步编程是实现高效并发处理的一种方法,它使得程序能够在等待 I/O 操作时继续执行其他任务。在 Python 中,asyncio 库是实现异步编程的主要工具。asyncio 提供了一种机制来编写可以在单线程内并发执行的代码,适用于 I/O 密集型任务。…...
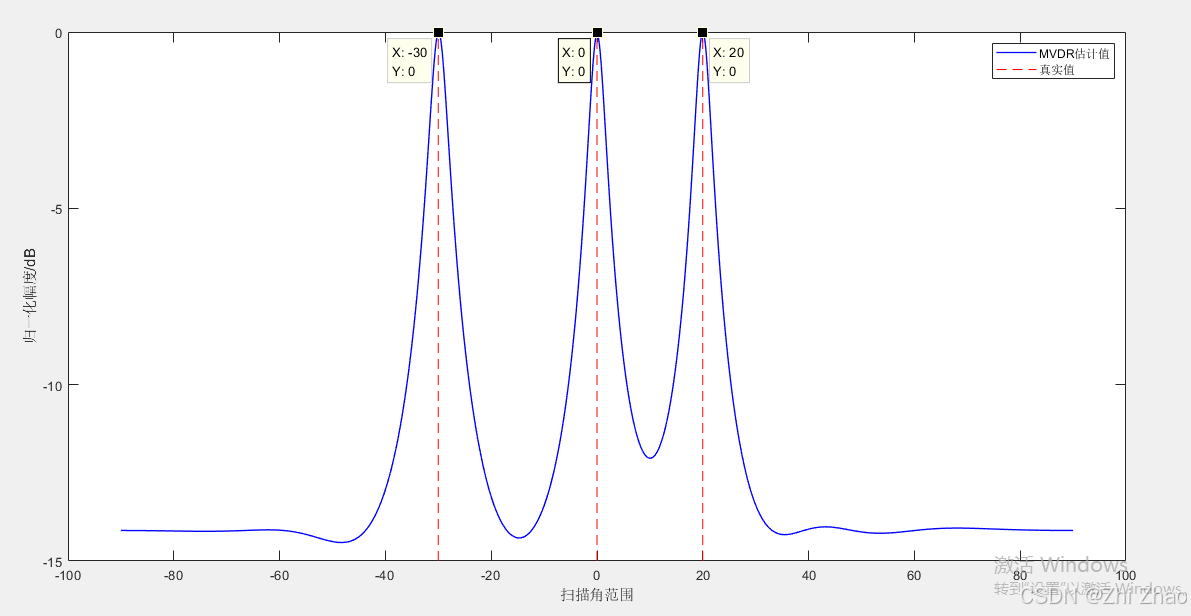
【信号频率估计】MVDR算法及MATLAB仿真
目录 一、MVDR算法1.1 简介1.2 原理1.3 特点1.3.1 优点1.3.2 缺点 二、算法应用实例2.1 信号的频率估计2.2 MATLAB仿真代码 三、参考文献 一、MVDR算法 1.1 简介 最小方差无失真响应(Mininum Variance Distortionless Response,MVDR)算法最…...
HarmonyOS NEXT零基础入门到实战-第二部分
HarmonyOS NEXT零基础入门到实战-第二部分 Swiper 轮播组件 Swiper是一个 容器 组件,当设置了多个子组件后,可以对这些 子组件 进行轮播显示。(文字、图片...) 1、Swiper基本语法 2、Swiper常见属性 3、Swiper样式自定义 4、案例&…...
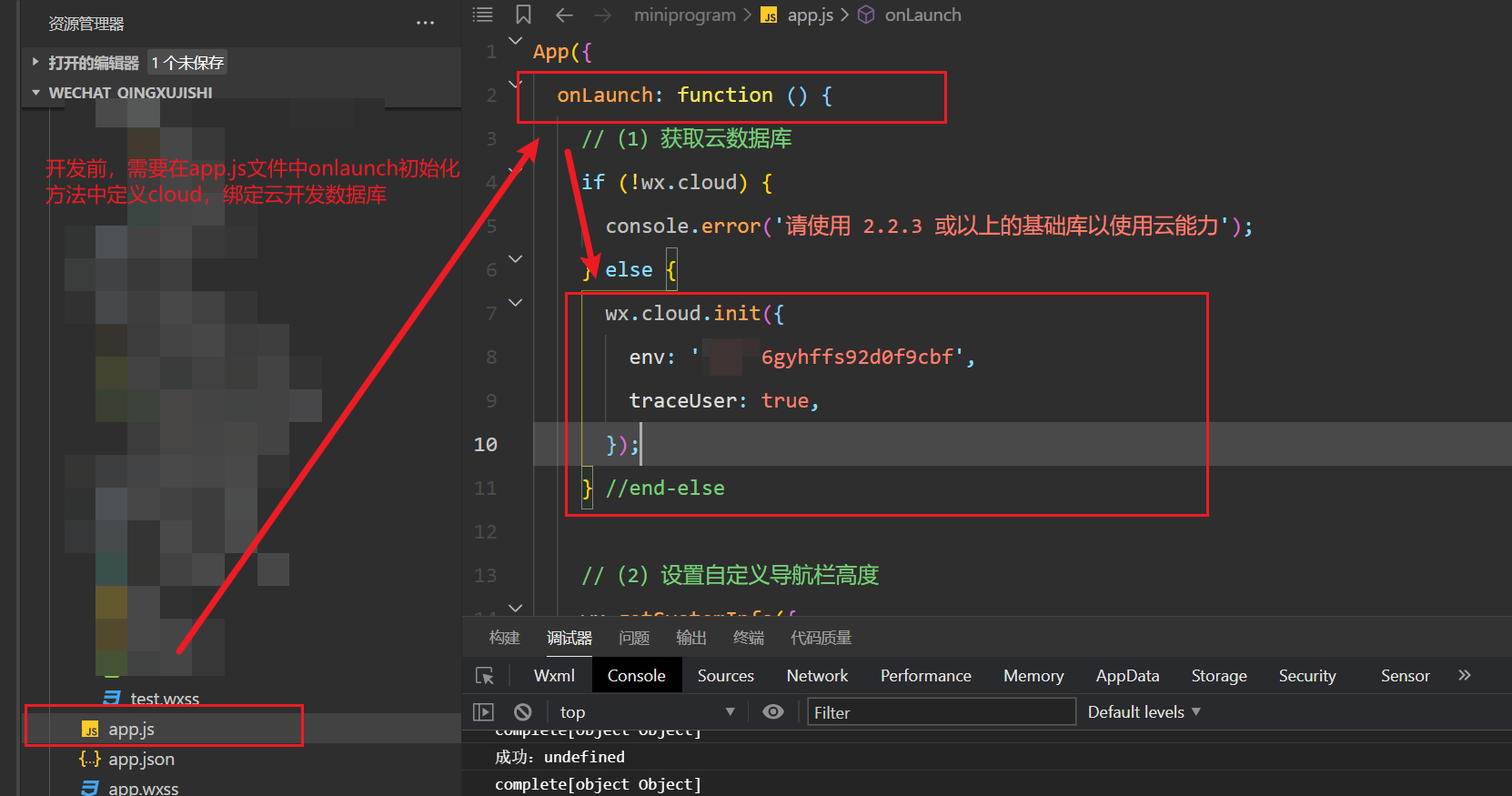
《小程序02:云开发之增删改查》
一、前置操作 // 一定要用这个符号包含里面的${}才会生效 wx.showToast({title: 获取数据成功:${colorLista}, })1.1:初始化介绍 **1、获取数据库引用:**在开始使用数据库 API 进行增删改查操作之前,需要先获取数据库的引用 cons…...
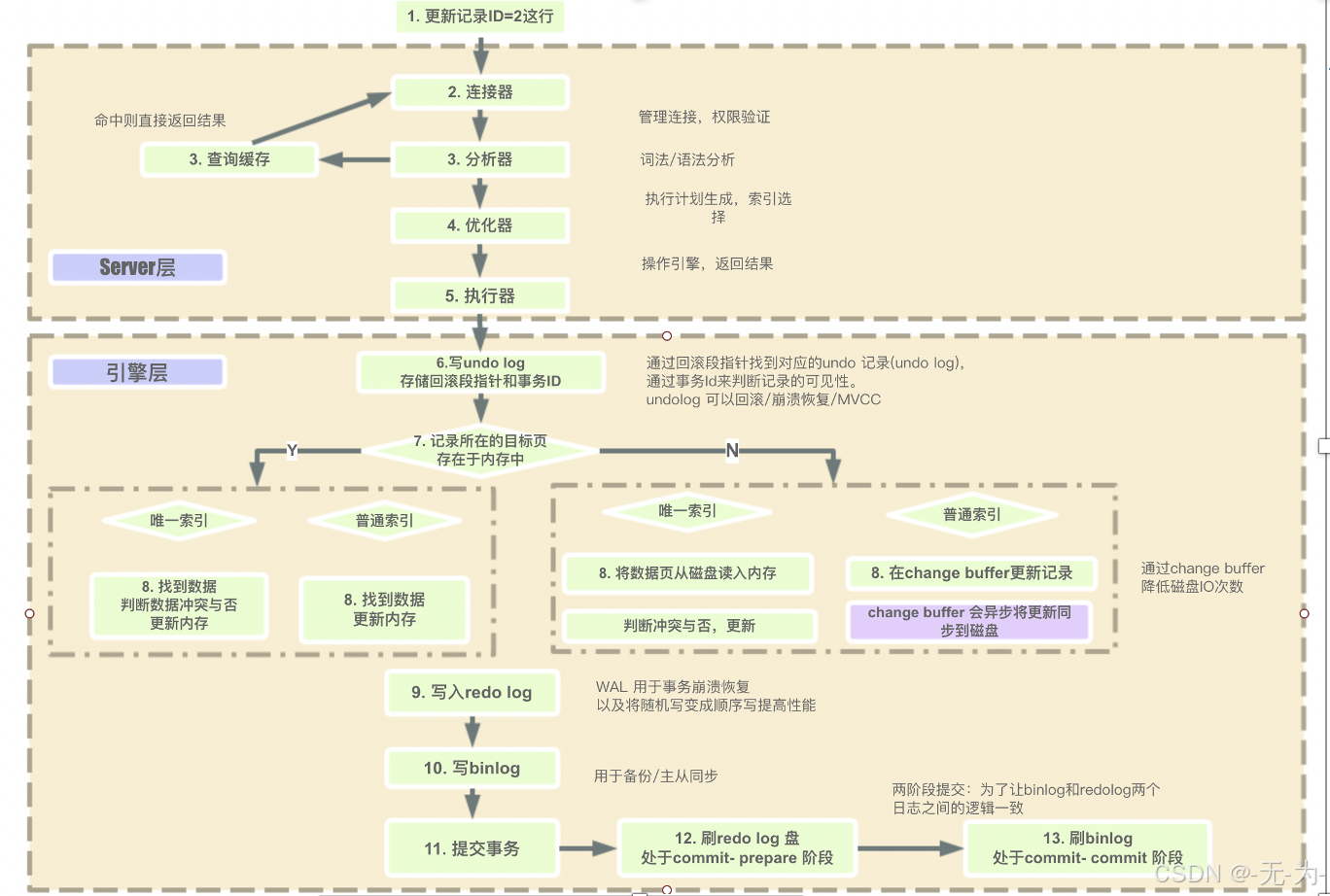
SQL执行流程、SQL执行计划、SQL优化
select查询语句 select查询语句中join连接是如何工作的? 1、INNER JOIN 返回两个表中的匹配行。 2、LEFT JOIN 返回左表中的所有记录以及右表中的匹配记录。 3、RIGHT JOIN 返回右表中的所有记录以及左表中的匹配记录。 4、FULL OUTER JOIN 返回左侧或右侧表中有匹…...

【前端】JavaScript入门及实战41-45
文章目录 41 嵌套的for循环42 for循环嵌套练习(1)43 for循环嵌套练习(2)44 break和continue45 质数练习补充 41 嵌套的for循环 <!DOCTYPE html> <html> <head> <title></title> <meta charset "utf-8"> <script type"…...
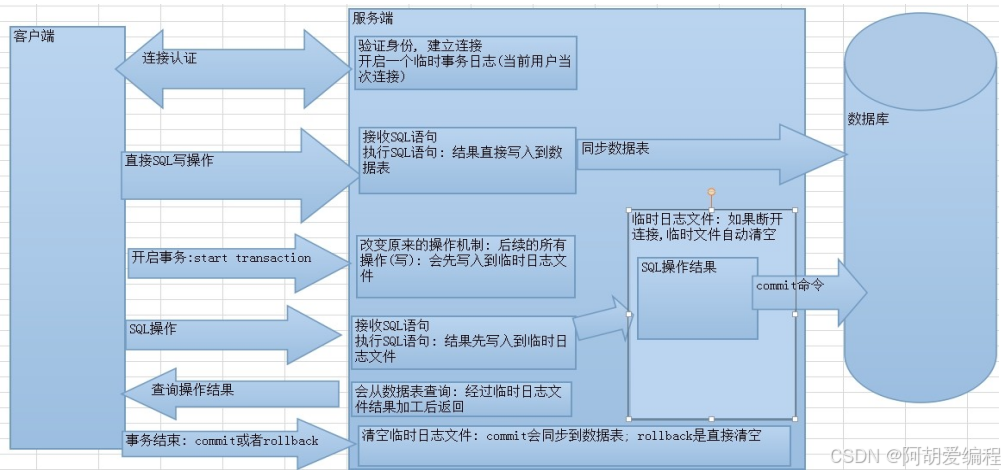
更加深入Mysql-04-MySQL 多表查询与事务的操作
文章目录 多表查询内连接隐式内连接显示内连接 外连接左外连接右外连接 子查询 事务事务隔离级别 多表查询 有时我们不仅需要一个表的数据,数据可能关联到俩个表或者三个表,这时我们就要进行夺标查询了。 数据准备: 创建一个部门表并且插入…...

基于最新版的flutter pointycastle: ^3.9.1的AES加密
基于最新版的flutter pointycastle: ^3.9.1的AES加密 自己添加pointycastle: ^3.9.1库config.dartaes_encrypt.dart 自己添加pointycastle: ^3.9.1库 config.dart import dart:convert; import dart:typed_data;class Config {static String password 成都推理计算科技; // …...

K8S内存资源配置
在 Kubernetes (k8s) 中,资源请求和限制用于管理容器的 CPU 和内存资源。配置 CPU 和内存资源时,使用特定的单位来表示资源的数量。 CPU 资源配置 CPU 单位:Kubernetes 中的 CPU 资源以 “核” (cores) 为单位。1 CPU 核心等于 1 vCPU/Core…...

【多任务YOLO】 A-YOLOM: You Only Look at Once for Real-Time and Generic Multi-Task
You Only Look at Once for Real-Time and Generic Multi-Task 论文链接:http://arxiv.org/abs/2310.01641 代码链接:https://github.com/JiayuanWang-JW/YOLOv8-multi-task 一、摘要 高精度、轻量级和实时响应性是实现自动驾驶的三个基本要求。本研究…...

数学建模--灰色关联分析法
目录 简介 基本原理 应用场景 优缺点 优点: 缺点: 延伸 灰色关联分析法在水质评价中的具体应用案例是什么? 如何克服灰色关联分析法在主观性强时的数据处理和改进方法? 灰色关联分析法与其他系统分析方法(如A…...
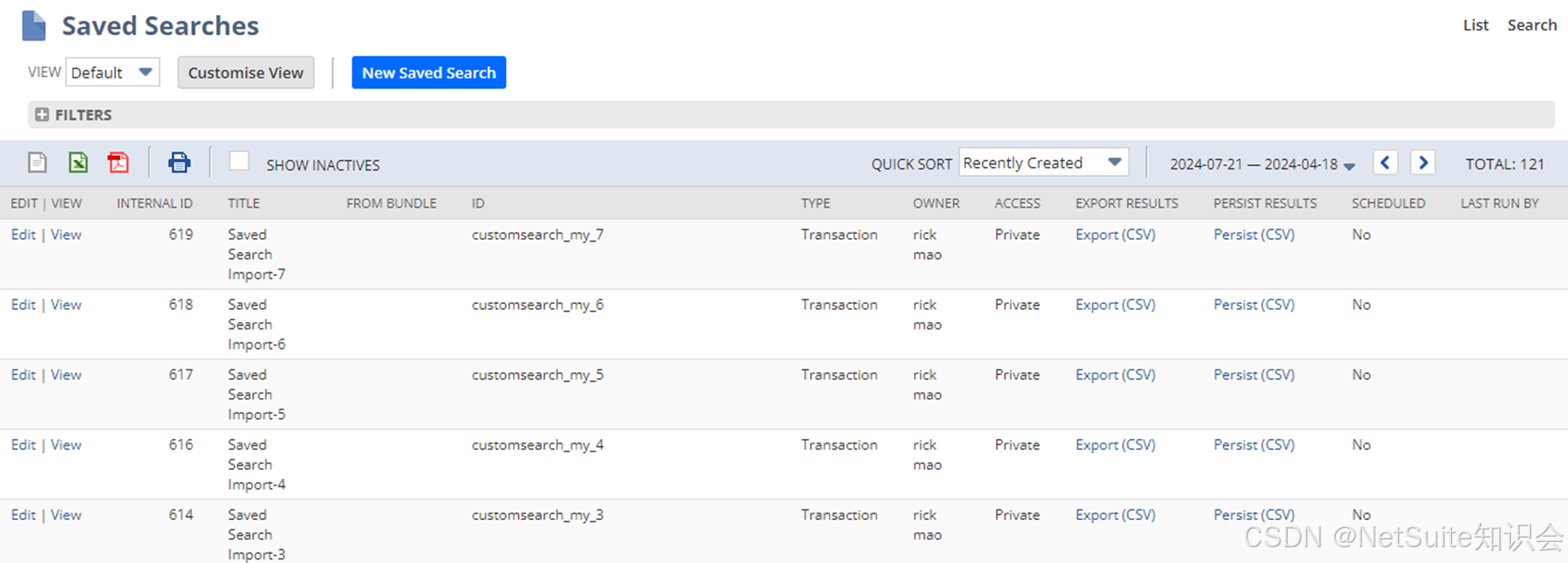
NetSuite Saved Search迁移工具
我们需要在系统间迁移Saved Search,但是采用Copy To Account或者Bundle时,会有一些Translation不能迁移,或者很多莫名其妙的Dependency,导致迁移失败。因此,我们想另辟蹊径,借助代码完成Saved Search的迁移…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

