均值滤波算法及实现
均值滤波器的使用场景:
均值滤波器使用于处理一些如上述蓝色线的高斯噪声场景
红色曲线是经过均值滤波处理后的数据。主要因为均值滤波设置数据缓冲区(也即延时周期),使得测量值经过缓冲不会出现特别大的变化。
黄色曲线为高斯噪声,红色曲线为经过均值滤波处理后的数据。
如果想要更好的滤波效果:
- 增加滤波和,也即往后多取几帧数据进行累加求和,再处以累加次数;
- 嵌套使用均值滤波,也即用上一均值滤波输出作为本次滤波输入;
均值滤波不适合处理类似橙色曲线的脉冲噪声的数据
蓝色曲线为经过均值滤波处理后的数据,虽然整体幅值降低了,但是如61-69区间,实际测量只在61附近出现一次突变,但很快下降正常,但经过均值滤波处理,虽然幅值被降低,但其实也没有达到理想,反而将突变脉冲以一个恒定的值持续了9s(累加次数,也即缓冲周期)。
目标脉冲值是0,未经过均值滤波处理在61s出现一较大突变,由于系统本身的阻尼等作用,系统实际不会产生太大的振荡,可能由于来的比较快,系统会微微抖一下就稳定。但如果使用均值滤波处理后,在61s处的尖峰脉冲硬是被拉长了9帧才退出,系统稳定性必定太差。因此脉冲信号噪声不适合用均值滤波,可以考虑使用低通滤波!
均值滤波作用
均值滤波是一种常见的图像处理技术,用于平滑图像中的噪声或细节。它的主要用途包括:
去除噪声:图像中的噪声是由于图像采集过程中的各种因素引入的不希望的干扰。均值滤波可以通过计算像素周围邻域内像素的平均值来平滑图像,并减少噪声的影响。
平滑图像:在某些情况下,图像中的细节过多或变化过于剧烈,可能会导致视觉上的不连续或不平滑感觉。均值滤波可以通过平均周围像素的值来减少这些细节,使图像更加平滑。
降低图像分辨率:在一些应用中,需要降低图像的分辨率以减少计算或存储的需求。均值滤波可以通过对图像进行平滑来实现降低分辨率的效果。
图像预处理:在某些图像处理任务中,如图像分割或边缘检测,均值滤波可以作为预处理步骤,帮助提取更准确的特征或边缘。
需要注意的是,均值滤波是一种简单且常用的滤波方法,但它可能会导致图像细节的模糊或平滑化。对于某些应用场景,可能需要考虑其他更高级的滤波技术,以在平滑图像的同时保留更多的细节信息。
均值滤波实现:
#include <stdio.h> #include <stdlib.h>double* weightedMeanFilter(double* input, int length, int windowSize, double* weights) {double* output = (double*)malloc(length * sizeof(double)); // 创建新数组int halfWindowSize = windowSize / 2;for (int i = 0; i < length; i++) {double weightedSum = 0.0;double weightSum = 0.0;for (int j = i - halfWindowSize; j <= i + halfWindowSize; j++) {if (j >= 0 && j < length) {weightedSum += input[j] * weights[j - (i - halfWindowSize)];weightSum += weights[j - (i - halfWindowSize)];}}output[i] = weightedSum / weightSum; // 计算加权平均值}return output; }int main() {double input[] = {1.2, 2.3, 3.4, 4.5, 5.6};int length = sizeof(input) / sizeof(input[0]);int windowSize = 3;double weights[] = {0.1, 0.6, 0.3}; // 示例权重系数数组double* output = weightedMeanFilter(input, length, windowSize, weights);printf("Input: ");for (int i = 0; i < length; i++) {printf("%.2f ", input[i]);}printf("\nOutput: ");for (int i = 0; i < length; i++) {printf("%.2f ", output[i]);}free(output); // 释放动态分配的内存return 0; } /* Input: 1.20 2.30 3.40 4.50 5.60 Output: 1.57 2.52 3.62 4.72 5.44 */增加权重系数可以使均值滤波更加灵活,以更好地适应不同的应用场景和需求。具体来说,增加权重系数的意义包括:
强调重要区域:通过调整权重系数,可以使某些像素在计算均值时具有更大的贡献。这样可以使均值滤波更加关注重要的区域,从而保留或突出这些区域的细节。例如,在人脸识别中,可以增加权重系数以突出人脸区域,以便更好地提取人脸特征。
抑制噪声或异常值:某些像素可能受到噪声或异常值的干扰,导致它们的值与周围像素明显不同。通过降低这些像素的权重系数,可以减少它们对均值的影响,从而抑制噪声或异常值的影响。
考虑空间相关性:在一些情况下,像素之间的空间关系对滤波结果的影响很大。通过调整权重系数以考虑像素之间的空间相关性,可以更好地保留图像的结构信息。例如,可以使用高斯加权系数来加权计算均值,以便更好地平滑图像并保留边缘。
自适应滤波:通过根据像素的特征或属性来动态调整权重系数,可以实现自适应滤波。这意味着不同的像素可以具有不同的权重,从而使滤波更加适应图像的局部特征。例如,可以根据像素的梯度值或纹理信息来调整权重系数,以实现更好的平滑效果。
总之,增加权重系数可以提供更多的灵活性和控制力,使均值滤波能够更好地适应不同的图像处理需求,并在平滑图像的同时保留重要的细节。
#include <stdio.h> #include <stdlib.h>double* weightedMeanFilter(double* input, int length, int windowSize, double* weights) {double* output = (double*)malloc(length * sizeof(double)); // 创建新数组int halfWindowSize = windowSize / 2;for (int i = 0; i < length; i++) {double weightedSum = 0.0;double weightSum = 0.0;for (int j = i - halfWindowSize; j <= i + halfWindowSize; j++) {if (j >= 0 && j < length) {weightedSum += input[j] * weights[j - (i - halfWindowSize)];weightSum += weights[j - (i - halfWindowSize)];}}output[i] = weightedSum / weightSum; // 计算加权平均值}return output; }int main() {double input[] = {1.2, 2.3, 3.4, 4.5, 5.6};int length = sizeof(input) / sizeof(input[0]);int windowSize = 3;double weights[] = {0.1, 0.6, 0.3}; // 示例权重系数数组double* output = weightedMeanFilter(input, length, windowSize, weights);printf("Input: ");for (int i = 0; i < length; i++) {printf("%.2f ", input[i]);}printf("\nOutput: ");for (int i = 0; i < length; i++) {printf("%.2f ", output[i]);}free(output); // 释放动态分配的内存return 0; } /* Input: 1.20 2.30 3.40 4.50 5.60 Output: 1.57 2.52 3.62 4.72 5.44 */
结果对比:
参考:
1、简单的均值滤波讲解(附代码)_哔哩哔哩_bilibili
2、https://www.cnblogs.com/faithlocus/p/17532226.html
相关文章:

均值滤波算法及实现
均值滤波器的使用场景: 均值滤波器使用于处理一些如上述蓝色线的高斯噪声场景 红色曲线是经过均值滤波处理后的数据。主要因为均值滤波设置数据缓冲区(也即延时周期),使得测量值经过缓冲不会出现特别大的变化。 黄色曲线为高斯噪声…...

【Apache Doris】周FAQ集锦:第 16 期
【Apache Doris】周FAQ集锦:第 16 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目! 在这个栏目中,每周将筛选社区反馈的热门问题和话题,重点回答并进行深入探讨。旨在为广大用户…...

单例模式_Golang
目录 一、单例模式 1.1 基本概念 1.2 使用场景 二、Golang实现 2.1 懒汉模式(Lazy Loading) 一、单例模式 1.1 基本概念 一个类只能生成一个实例,且该类能自行创建这个实例的一种模式,这个定义个人感觉可以拆的通俗一些,在项目的生命周…...
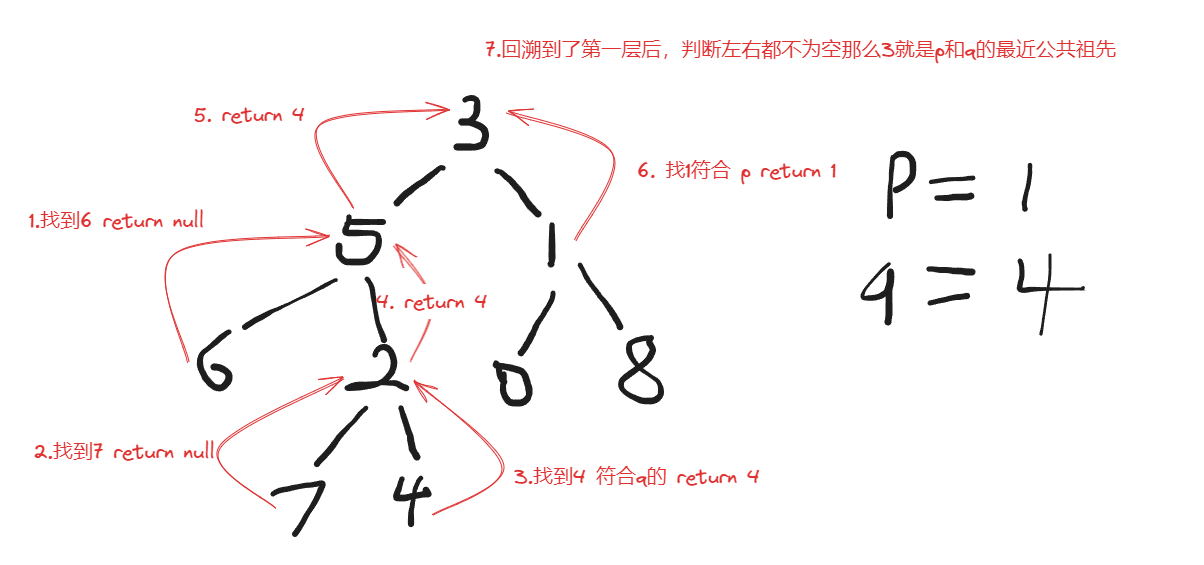
代码随想录 day 18 二叉树
第六章 二叉树part06 详细布置 530.二叉搜索树的最小绝对差 需要领悟一下二叉树遍历上双指针操作,优先掌握递归 题目链接/文章讲解:https://programmercarl.com/0530.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E7%B…...

降雨量预测 | Matlab基于ARIMA-RBF降雨量预测
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 降雨量预测 | Matlab基于ARIMA-RBF降雨量预测 注:程序和数据放在一个文件夹。 程序语言为matlab,程序可出预测效果图,指标图; 代码特点:参数化编程、参数可方便更改、代…...

包含示例和模板的流程文档指南
当您的业务扩展时,您会得到越来越多的移动部件,并且需要有人来跟踪复杂性。人员和任务需要以尽可能最高效的方式进行组织,并且您必须找到某种方法让员工知道如何执行有效完成工作所需的流程。 为了使流程可重复,需要对其进行记录…...

51单片机嵌入式开发:15、STC89C52RC操作蜂鸣器实现一个music音乐播放器的音乐盒
STC89C52RC操作蜂鸣器实现一个music音乐播放器的音乐盒 1 概述2 蜂鸣器操作方法3 蜂鸣器发出音声4 硬件电路5 软件实现6 整体工程:7 总结 1 概述 要实现一个基于STC89C52RC单片机的音乐盒,可以按照以下步骤进行: (1)硬…...
数据结构)
B树(B-Tree)数据结构
1. 什么是B树? B树(B-Tree)是一种多路搜索树,用于存储和检索大量数据。它是自适应的,适用于各种存储设备和各种数据量。B树的特点是高效的搜索、插入和删除操作,且可以在各种情况下保持树的平衡。 2. B树…...

【BUG】已解决:ModuleNotFoundError: No module named ‘torch‘
已解决:ModuleNotFoundError: No module named ‘torch‘ 欢迎来到英杰社区https://bbs.csdn.net/topics/617804998 欢迎来到我的主页,我是博主英杰,211科班出身,就职于医疗科技公司,热衷分享知识,武汉城市…...

数据结构——队列(链式结构)
一、队列链式结构定义 队列的链式存储结构是一种用链表实现的队列,它不像顺序存储结构那样需要预先分配固定大小的空间。链式存储结构的队列由节点组成,每个节点包括数据和指向下一个节点的指针。队列的链式存储结构可以动态地分配内存,更灵活地处理数据。在链式存储结构中…...

解决GoLand添加GOROOT提示The selected directory is not a valid home for Go Sdk的问题
现象 解决 在Go安装路径下找到zversion.go文件,我的在D:\Program Files\Go1.21.1\src\runtime\internal\sys下面 打开文件,添加如下内容: const TheVersion go1.21.1保存后再重新添加GOROOT即可...

51单片机(STC8H8K64U/STC8051U34K64)_RA8889驱动TFT大屏_I2C_HW参考代码(v1.3) 硬件I2C方式
本篇介绍单片机使用硬件I2C方式控制RA8889驱动彩屏。 提供STC8H8K64U和STC8051U34K64的参考代码。 【硬件部份】STC8H8K64U/STC8051U34K64 RA8889开发板 7寸TFT 800x480 1. 实物连接图:STC8H8K64URA8889开发板,使用P2口I2C接口: 2.实物连…...

【Python其他检查字符串占字节数的方法】
在Python中,检查字符串在特定编码下占用的字节数,最标准且常用的方法是通过字符串的.encode()方法将字符串转换为字节串,然后使用len()函数来获取这个字节串的长度。这是因为字符串(在Python 3中)是以Unicode形式存储的…...

梧桐数据库: 数据库技术中的重写子查询技术
数据库技术中的重写子查询技术,是数据库查询优化的一种重要手段。该技术主要通过改变子查询的形式,使其在执行效率和性能上得到优化。以下是对重写子查询技术的详细解析: 一、定义与目的 定义:重写子查询技术是指在数据库查询优…...

PHP连接MySQL数据库
PHP本身不具备操作MySQL数据库的能力,需要借助MySQL扩展来实现。 1、PHP加载MySQL扩展:php.ini文件中。(不要用记事本打开) 2、PHP中所有扩展都是在ext的文件夹中,需要指定扩展所在路径:extension_dir。 3、…...

STM32自己从零开始实操:PCB全过程
一、PCB总体分布 以下只能让大家看到各个模块大致分布在板子的哪一块,只能说每个人画都有自己的理由: 电源:从外部接入电源,5V接到中间,向上变成4V供给无线,向下变成3V供给下面的接口(也刻意放…...

error `slot` attributes are deprecated vue/no-deprecated-slot-attribute
旧的代码如下: <template slot"title">{{ item.title }}</template> {{ item.title }} 是一个模板标签,它在模板中插入了一个元素(slot),并指定了元素的名称为 “title”。这个标签在模板中显示…...

Websocket自动消息回复服务端工具
点击下载《Websocket自动消息回复服务端工具》 1. 前言 在进行Websocket开发时,前端小伙伴通常是和后端开发人员同步进行项目开发,经常会遇到后端开发人员接口还没开发完,也没有可以调试的环境,只能按照接口文档进行“脑回路开发…...

【软考】UML中的关联关系
目录 一、说明二、具体类型2.1 普通关联2.2 单向关联2.3 双向关联2.4 自关联2.4 聚合关系(Aggregation)2.5 组合关系(Composition) 三、关联关系中的多重性 一、说明 1.UML(Unified Modeling Language,统一…...

贪吃蛇超精讲(C语言)
前言 如果你还是个萌新小白,那么该项目的攻克过程一定会十分艰难。虽然作者已经将文章尽可能写的逻辑清晰,内容详细。但所谓“纸上得来终觉浅”,在讲到陌生结构和函数时,大家请一定自己动手去敲一遍代码,这很重要&…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...




