浏览器的卡顿与react的解决思路
以下内容是阅读过程中结合自己的思考而诞生的产物,不一定准确,但相反的,可能个人对实际情况有很大的误解。
仅做参考,欢迎指正。
前面提到浏览器显示的其实是渲染流程最后渲染出来的一张图片,而一个行为引起的副作用需要生成的最终图片,可以以多个进度的快照图片逐渐渲染出最终图片来,也可以完全准备好再直接渲染出来。
当这种‘逐渐’过程中卡顿的时间或者完全准备好卡顿的时间低于人眼感知极限的时候,页面渲染流程对于人来说就是‘丝滑顺畅’的。
人眼感知极限在200多赫兹,即每秒200多张图片,但实际上当超过60hz时,人眼对其感知就不那么明显了,而要分别60hz以上的区别时,还容易让人产生疲劳,所以60hz仍是主流。
什么是卡顿
众所都周知,js是单线程,当react处理vdom相关工作的时候,会阻塞浏览器的渲染过程,阻塞了渲染过程,那么页面就卡着。
结合上面所述,1秒60hz,相当于16.67ms至少需要渲染出1张新图,才不会觉的卡顿。
我理解这里的卡顿,并不是说优化的怎么怎么好让总工作量少了,处理的快了,而是可能虽然每次渲染出来的新内容少,但是他仍然在生成,而不会在处理过程中一直不变,然后突然渲染出来,这种抖动的、掉帧的渲染方式,容易让人觉的他卡了,而一直在变化,虽然每次变化的不多,但总体是‘流畅的’
如何避免‘抖动型卡顿’
如何解决这个问题呢?每个人设备性能是不一样的,react处理vdom相关工作时速度不一样的,显然无法从设备硬件入手;那优化react,各种处理都使用最优方案,但工作量一多、设备性能一差,该卡照样卡。
其实由上面粗体字的叙述,我理解优化思路是,硬件差处理慢,OK没问题,处理的东西多,OK也没问题,那我每次都处理一丢丢,然后你去生成图片,然后我再处理一丢丢,而且每次都卡人眼感知极限,让你感觉不到抖动或者说掉帧,这不就完了吗?
于是便诞生了时间切片
时间切片
将vdom相关的处理工作,拆分为一个个单独的宏任务(参见事件循环),将这里的每个宏任务都限制在一定的范围内(react初始为5ms),而每个任务执行完后,将执行权限交给浏览器, 让浏览器生成当前的一张图片。
那么,如果一个长任务,即便在a主机上执行需要50ms,而在b主机上执行需要100ms,那么在这种硬件设备差距悬殊的情况下,这种思路依然有效。
思考
以下为个人思考:
分给react执行的时间还是相对较少,虽然规避了掉帧,但是这种行为效率并不是很高,为了执行5ms的react任务,需要花费十来毫秒去走一遍浏览器渲染流程。
我觉得是不是能把渲染流程与脚本行为分离,让脚本一直执行,而每次渲染流程执行完后,如果发现还有脚本任务在跑,则拿取当前dom结构的快照,继续去渲染。
但这其实就不是单线程了吧。不知道是否合理或者能否实现,还需要继续阅读 & 学习。
相关文章:

浏览器的卡顿与react的解决思路
以下内容是阅读过程中结合自己的思考而诞生的产物,不一定准确,但相反的,可能个人对实际情况有很大的误解。 仅做参考,欢迎指正。 前面提到浏览器显示的其实是渲染流程最后渲染出来的一张图片,而一个行为引起的副作用需…...

XXE:XML外部实体引入
XXE漏洞 如果服务器没有对客户端的xml数据进行限制,且版本较低的情况下,就可能会产生xxe漏洞 漏洞利用流程 1.客户端发送xml文件,其中dtd存在恶意的外部实体引用 2.服务器进行解析 3.服务器返回实体引用内容 危害:任意文件读…...

3D培训大师创新培训体验,加速空调关键组件的高效精准安装
如今,空调系统的复杂性和精密性与日俱增,对专业技术人员的要求也日益提高。尤其是决定空调是否能平稳运行的空调关键组件的装配培训,不再局限于传统的理论讲解和实体模型演示,而是更注重数字化、沉浸式学习。 案例背景 某空调公…...

PyTorch 深度学习实践-循环神经网络(高级篇)
视频指路 参考博客笔记 参考笔记二 文章目录 上课笔记总代码练习 上课笔记 个人能力有限,重看几遍吧,第一遍基本看不懂 名字的每个字母都是一个特征x1,x2,x3…,一个名字是一个序列 rnn用GRU 用ASCII表作为词典,长度为128&#x…...

这才是老板喜欢的电子信息类简历
点击可直接使用...

MySQL学习之事务,锁机制
事务 什么是事务? 事务就是逻辑上的一组操作,要么全做,要么全不做 事务经典例子:转账,转账需要两个操作,从一个人账户上减钱,在另一个账户上加钱,比如说小红给小明转账100元&…...

开源知识付费小程序源码 内容付费系统php源码 含完整图文部署教程
在当今数字化时代,知识付费作为一种新型的经济模式,正逐渐受到越来越多内容创作者、专家及商家的青睐。开源知识付费小程序源码和内容付费系统PHP源码作为实现这一模式的重要工具,为构建高效、安全、可扩展的知识付费平台提供了强大的技术支持…...

时序数据库如何选型?详细指标总结!
工业物联网场景,如何判断什么才是好的时序数据库? 工业物联网将机器设备、控制系统与信息系统、业务过程连接起来,利用海量数据进行分析决策,是智能制造的基础设施,并影响整个工业价值链。工业物联网机器设备感知形成了…...

【前端】JavaScript入门及实战51-55
文章目录 51 函数52 函数的参数53 返回值54 练习55 return 51 函数 <!DOCTYPE html> <html> <head> <title></title> <meta charset "utf-8"> <script type"text/javascript">/* 函数:1. 函数也是…...

【引领未来智造新纪元:量化机器人的革命性应用】
在日新月异的科技浪潮中,量化机器人正以其超凡的智慧与精准的操作,悄然改变着各行各业的生产面貌,成为推动产业升级、提升竞争力的关键力量。今天,让我们一同探索量化机器人在不同领域的广泛应用价值,见证它如何以科技…...

山东航空小程序查询
山东航空小程序 1) 请求地址 https://scxcx.sda.cn/mohe/proxy?url/trp/ticket/search 2) 调用方式:HTTP post 3) 接口描述: 接口描述详情 4) 请求参数: {"dep": "TAO","arr": "HRB","flightDate&qu…...

MySQL添加索引时会锁表吗?
目录 简介Online DDL概念Online DDL用法总结 简介 在MySQL5.5以及之前的版本,通常更改数据表结构操作(DDL)会阻塞对表数据的增删改操作(DML)。 MySQL5.6提供Online DDL之后可支持DDL与DML操作同时执行,降低…...
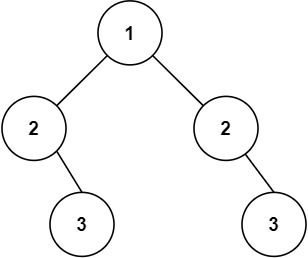
算法日记day 16(二叉树的广度优先遍历|反转、对称二叉树)
一、二叉树的层序遍历 题目: 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3]…...

PolarisMesh源码系列--Polaris-Go注册发现流程
导语 北极星是腾讯开源的一款服务治理平台,用来解决分布式和微服务架构中的服务管理、流量管理、配置管理、故障容错和可观测性问题。在分布式和微服务架构的治理领域,目前国内比较流行的还包括 Spring Cloud,Apache Dubbo 等。在 Kubernete…...

vue3 vxe-grid修改currentPage,查询数据的时候,从第一页开始查询
1、当我们设置好VxeGrid.Options进行数据查询的时候,下面是可能的设置: const gridOptions reactive<BasicTableProps>({id: UserTable,showHeaderOverflow: false,showOverflow: true,keepSource: true,columns: userColumns,size: small,pagerConfig: {cur…...
电商数据集成之电商商品信息采集系统架构设计||电商API接口
一、引言 本架构设计文档旨在阐述基于 Selenium 的电商商品信息采集系统的整体架构,包括系统视图、逻辑视图、物理视图、开发视图和进程视图,并提供一个简单的采集电商商品信息的 demo。该系统通过模拟浏览器行为,实现对电商商品信息的自…...

Spring Cloud Stream 实现统一消息通信平台
1. 概述 Spring Cloud Stream:是Spring提供的消息通信框架,旨在构建跨不同消息中间件的统一通信平台。目的:通过消息通信机制降低分布式系统中服务间的耦合度,实现异步服务交互。 2. 消息通信与RPC RPC:远程过程调用…...

uniapp安卓plus原生选择系统文件
uniapp安卓plus原生选择系统文件 效果: 组件代码: <template xlang"wxml" minapp"mpvue"><view></view> </template> <script>export default {name: file-manager,props: {},data() {return {is…...

Go语言 Import导入
本文主要介绍Go语言import导入使用时注意事项和功能实现示例。 目录 Import 创建功能文件夹 加法 减法 主函数 优化导入的包名 .引入方法 总结 Import 创建功能文件夹 做一个计算器来演示,首先创建test文件夹。 加法 在test文件夹中创建add文件夹ÿ…...
一款异次元小清新风格的响应式wordpress个人博客主题
一款异次元小清新风格的响应式个人博客主题。这是一款专注于用户阅读体验的响应式 WordPress 主题,整体布局简洁大方,针对资源加载进行了优化。 Kratos主题基于Bootstrap和Font Awesome的WordPress一个干净,简单且响应迅速的博客主题&#x…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
