Java | Leetcode Java题解之第268题丢失的数字
题目:

题解:
class Solution {public int missingNumber(int[] nums) {int n = nums.length;int total = n * (n + 1) / 2;int arrSum = 0;for (int i = 0; i < n; i++) {arrSum += nums[i];}return total - arrSum;}
}相关文章:

Java | Leetcode Java题解之第268题丢失的数字
题目: 题解: class Solution {public int missingNumber(int[] nums) {int n nums.length;int total n * (n 1) / 2;int arrSum 0;for (int i 0; i < n; i) {arrSum nums[i];}return total - arrSum;} }...

指针!!C语言(第二篇)
目录 一. 数组名的理解 二. 一维数组传参的本质 三. 冒泡排序法 四. 二级指针与指针数组 五. 字符指针变量与数组指针 一. 数组名的理解 在我们对指针有了初步的理解之外,今天我们来掌握一些新的知识就是数组与指针,第一个对数组名的了解ÿ…...

AIGC-ToonCrafter: Generative Cartoon Interpolation
论文:https://arxiv.org/pdf/2405.17933 代码:https://doubiiu.github.io/projects/ToonCrafter 给定首尾帧,生成逼真生动的动画 MOTIVATION Traditional methods which implicitly assume linear motion and the absence of complicated phenomena like disoccl…...
)
牛奶供应(三)
一个字贪,第一天,只能选择制作方式,后面的每一天,在<今天制作>与<前期存储>之间取更优解 例如样例:100 5,200 5,90 20,存储成本为10 第1天: 一定是制作&…...

首批通过 | 百度通过中国信通院H5端人脸识别安全能力评估工作
2024年5月,中国信息通信研究院人工智能研究所依托中国人工智能产业发展联盟安全治理委员会(AIIA)、“可信人脸应用守护计划”及多家企业代表共同开展《H5端人脸识别线上身份认证安全能力要求及评估方法》的编制工作,并基于该方法开…...

JVM---对象是否存活及被引用的状态
1.如何判断对象是否存活 1.1 引用计数算法 概念:在对象头部增加一个引用计数器,每当有一个地方引用它时,计数器值就加一;当引用失效时,计数器值就减一;任何时刻计数器为零的对象就是不可能再被使用的。 优点࿱…...

科研绘图系列:R语言分割小提琴图(Split-violin)
介绍 分割小提琴图(Split-violin plot)是一种数据可视化工具,它结合了小提琴图(violin plot)和箱线图(box plot)的特点。小提琴图是一种展示数据分布的图形,它通过在箱线图的两侧添加曲线来表示数据的密度分布,曲线的宽度表示数据点的密度。而分割小提琴图则是将小提…...
WEB前端09-前端服务器搭建(Node.js/nvm/npm)
前端服务器的搭建 在本文中,我们将介绍如何安装和配置 nvm(Node Version Manager)以方便切换不同版本的 Node.js,以及如何设置 npm(Node Package Manager)使用国内镜像,并搭建一个简单的前端服…...

ASP.NET Core在启动过程中使用数据库实例的几种方式
ASP.NET Core项目启动过程中若要调用SqlSugarClient实例操作数据库数据(假设操作函数如下),特此记录以下几种方式: public class PublicDataBuffer {public static List<EnvironmentRecord> DataBuffer new List<Envir…...

AndroidStudio 编辑xml布局文件卡死问题解决
之前项目编写的都是正常,升级AndroidStudio后编辑布局文件就卡死,还以为是AndroidStudio文件。 其实不然,我给整个项目增加了版权声明。所以全部跟新后,布局文件也增加了版权声明。估计AndroidStudio在 解析布局文件时候因为有版…...

使用 PVE 自签 CA 证书签发新证书
前言 PVE 安装时会自动创建一个有效期 10 年的 CA 证书, 我们可以利用这个 CA 证书给虚拟机中的 Web 应用签发新的 TLS 证书用于提供 HTTPS 服务. 下面以 PVE 虚拟机中通过 Docker 跑的一个 雷池 应用为例进行演示. PVE 证书位置 官方文档: https://pve.proxmox.com/wiki/Pr…...

ubuntu 22.04安装Eigen
1 安装 git clone https://gitlab.com/libeigen/eigen.gitcd eigen mkdir build cd build cmake ..sudo make install... -- Installing: /usr/local/include/eigen3/unsupported/Eigen/CXX11/src/TensorSymmetry -- Installing: /usr/local/include/eigen3/unsupported/Eige…...

vue使用audio 音频实现播放与关闭(可用于收到消息给提示音效)
这次项目中因为对接了即时通讯 IM,有个需求就是收到消息需要有个提示音效,所以这里就想到了用HTML5 提供的Audio 标签,用起来也是很方便,首先让产品给你个提示音效,然后你放在项目中,使用Audio 标签&#x…...

STM32 产生Hard Fault 调试方法
STM32 产生hard-fault 调试方法 需求 当STM32 产生Hard Fault的时候我们希望可以打印出一些重要的寄存器信息,然后定位代码出错的地方。 参考 https://github.com/ferenc-nemeth/arm-hard-fault-handler 原理 STM32代码运行的时候一般在是main函数while(1)中循…...

java-selenium 截取界面验证码图片并对图片文本进行识别
参考链接 1、需要下载Tesseract工具并配置环境变量,步骤如下 Tesseract-OCR 下载安装和使用_tesseract-ocr下载-CSDN博客 2、需要在IDEA中导入tess4j 包;在pom.xml文件中输入如下内容 <!--导入Tesseract 用于识别验证码--><dependency>&l…...

【Linux】进程信号 --- 信号产生
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和算法 ✈️专栏:Linux 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵,希望大佬指点一二 如果文章对…...

Docker 容器中的 Docker Compose 简介
Docker Compose是什么 Docker Compose是一个用于定义和运行多个Docker容器的工具。它是Docker官方提供的开源项目,用于实现对Docker容器集群的快速编排。通过Compose,开发者可以使用YAML文件(通常是docker-compose.yml文件)来配置…...

手机日历如何与Outlook同步
有很多人和我一样遇到手机日历与Outlook同步问题,如新版outlook与小米日历的同步问题 - Microsoft Community,outlook账号无法在手机端自带的电子邮件App以exchange模式登录 - Microsoft Community,在安卓手机端无法电子邮件App以exchange模式…...

python基础语法 007 文件操作-1读取写入
1 文件操作 1.1 什么时候用文件操作? 打开文档写东西看东西拿文档做统计 在python 文档操作作用 存储数据读取数据 打开文件有什么用? 读取数据,写入数据不管什么数据都可以用open打开,如可复制一张图片 1.2 open() 读取,…...

C语言·函数(超详细系列·全面总结)
前言:Hello大家好😘,我是心跳sy,为了更好地形成一个学习c语言的体系,最近将会更新关于c语言语法基础的知识,今天更新一下函数的知识点,我们一起来看看吧! 目录 一、函数是什么 &a…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
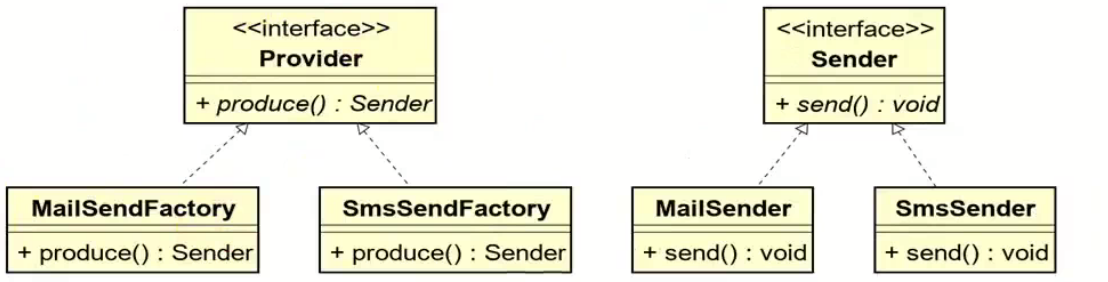
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
