如何使用aiohttp或requests-async等库并发地执行多个HTTP请求
在Python中,要并发地执行多个HTTP请求,可以使用aiohttp这样的异步HTTP客户端库,因为它支持异步编程,能够显著提高IO密集型任务的性能,比如网络请求。requests-async并不是一个广泛认知的库(虽然可能存在类似名称的库或自定义实现),但通常我们会使用aiohttp或httpx(后者也支持异步和同步请求)来实现异步HTTP请求。
以下是如何使用aiohttp来并发执行多个HTTP请求的示例:
安装aiohttp
首先,确保安装了aiohttp:
bash复制代码
pip install aiohttp |
示例代码
python复制代码
import aiohttp | |
import asyncio | |
async def fetch(session, url): | |
async with session.get(url) as response: | |
return await response.text() | |
async def main(): | |
urls = [ | |
'http://httpbin.org/get', | |
'http://httpbin.org/ip', | |
'http://httpbin.org/headers', | |
] | |
async with aiohttp.ClientSession() as session: | |
tasks = [fetch(session, url) for url in urls] | |
# 使用 asyncio.gather 来并发执行所有任务 | |
results = await asyncio.gather(*tasks) | |
for result in results: | |
print(result) | |
# Python 3.7+ | |
asyncio.run(main()) |
解释
-
导入必要的库:导入
aiohttp和asyncio。 -
定义异步函数:
fetch是一个异步函数,它接收一个aiohttp.ClientSession和一个URL,然后使用这个会话来发送GET请求并返回响应的文本内容。 -
主函数:
main函数是异步的,它首先定义了一个URL列表。然后,它使用aiohttp.ClientSession()创建了一个会话,并使用列表推导式为每个URL创建了一个fetch任务。 -
并发执行:使用
asyncio.gather来并发执行所有任务。asyncio.gather会等待所有任务完成,并返回一个包含所有任务结果的列表。 -
输出结果:遍历
results列表并打印每个结果。 -
运行主函数:使用
asyncio.run(main())来运行主函数。这是Python 3.7及以上版本中推荐的启动异步事件循环的方式。
注意事项
- 异步编程需要一定的时间来适应和理解,特别是当涉及到错误处理和资源管理(如会话和连接)时。
aiohttp库非常强大,支持许多高级功能,如Websockets、HTTP/2等。- 在生产环境中,你可能需要更复杂的错误处理和重试逻辑来确保请求的成功和系统的稳定性。
相关文章:

如何使用aiohttp或requests-async等库并发地执行多个HTTP请求
在Python中,要并发地执行多个HTTP请求,可以使用aiohttp这样的异步HTTP客户端库,因为它支持异步编程,能够显著提高IO密集型任务的性能,比如网络请求。requests-async并不是一个广泛认知的库(虽然可能存在类似…...

Golang | Leetcode Golang题解之第257题二叉树的所有路径
题目: 题解: func binaryTreePaths(root *TreeNode) []string {paths : []string{}if root nil {return paths}nodeQueue : []*TreeNode{}pathQueue : []string{}nodeQueue append(nodeQueue, root)pathQueue append(pathQueue, strconv.Itoa(root.V…...

关于css中flex布局垂直居中失效问题的原因
项目中遇到用flex进行页面布局后,使用上下居中设置:align-item: center; 目标效果如下: 但是失效,不起作用,如下图所示: 各种排查过后发现设置了子模块 align-self 属性,这会覆盖容器上的 al…...

用Redisson写一个库存扣减的方法
使用Redisson来处理库存操作可以确保在高并发环境下库存数据的一致性和完整性。以下是使用Redisson实现库存管理的一些通用方法,包括获取库存、扣减库存、设置库存等。我们将使用Redisson的ReentrantLock来确保并发安全。 首先,确保你已经正确设置了Red…...

第2节课:文本内容与格式化——HTML中的文本处理技巧
目录 文本内容与格式化:段落和标题:构建文本基础段落 <p>标题 <h1> 到 <h6> 格式化:强调和样式加粗 <b>斜体 <i>下划线 <u> 列表:组织内容无序列表 <ul>有序列表 <ol>定义列表 &…...

temu平台电池/锂电池UN38.3资质合规解析
UN38.3资质合规解析 为满足相关法律法规和商品运输安全需求含锂电池商品需要提供对应的UN38.3资质。截至7月29日,相关类目下UN38.3资质待上传或上传失败的商品可能面临下架。 -01什么是UN38.3- 1)UN38.3是指由联合国危险货物运输专家委员会编写的《试验…...

Huawei、Cisco 路由中 RIP 协议 summary 的用法
华为路由中 RIP summary summary用来使能 RIP 有类聚合,聚合后的路由以使用自然掩码的路由形式发布。undo summary用来取消有类聚合以便在子网之间进行路由,此时,子网的路由信息就会被发布出去。路由聚合降低了路由表中路由信息量。说明 有类…...
)
智能图像信息提取(飞桨OCR+ERNIE-Layout)
嘿,技术大佬们,今天我要分享的是一个超级棒的OCR技术方案,它结合了飞桨OCR和ERNIE-Layout,绝对是图像信息提取的利器! 线上体验地址:智能图像信息提取(飞桨OCRERNIE-Layout) 它基于ERNIE -Layout和多版本Pa…...

Ubuntu 24.04 LTS Noble安装 FileZilla Server
FileZilla Server 是一款使用图形用户界面快速创建 FTP 服务器的软件。它有助于测试需要 FTP 服务器功能的各种项目。虽然早期的 FileZilla FTP 服务器仅适用于 Windows 和 macOS,但现在我们也可以在 Linux(例如 Ubuntu 24.04)上安装 FileZil…...

【关于使用swoole的知识点整理】
目录 (1)Swoole 如何理解,能解决你项目中的哪些痛点? (2)Swoole里的协程是什么,怎么用?为什么协程可以提高并发? (3)简述Swoole有哪些优点&…...

迁移学习:目标检测的加速器
迁移学习:目标检测的加速器 在深度学习领域,目标检测是一项至关重要的任务,广泛应用于从视频监控到自动驾驶等众多领域。然而,训练一个高性能的目标检测模型不仅需要大量的标注数据,还需要大量的计算资源和时间。迁移…...

gitee的怎么上传项目
前提 1.先下载Git Bash (如果没有下载的宝子们下载连接如下: 链接: link ) 项目上传到Gitee步骤 1.在Gitee上建立远程仓库 2.填写相关信息 3.进入本地你想要上传的文件目录下,右键单击空白处,点击Git Bash Here 4.配置你的用户名和邮箱 git con…...
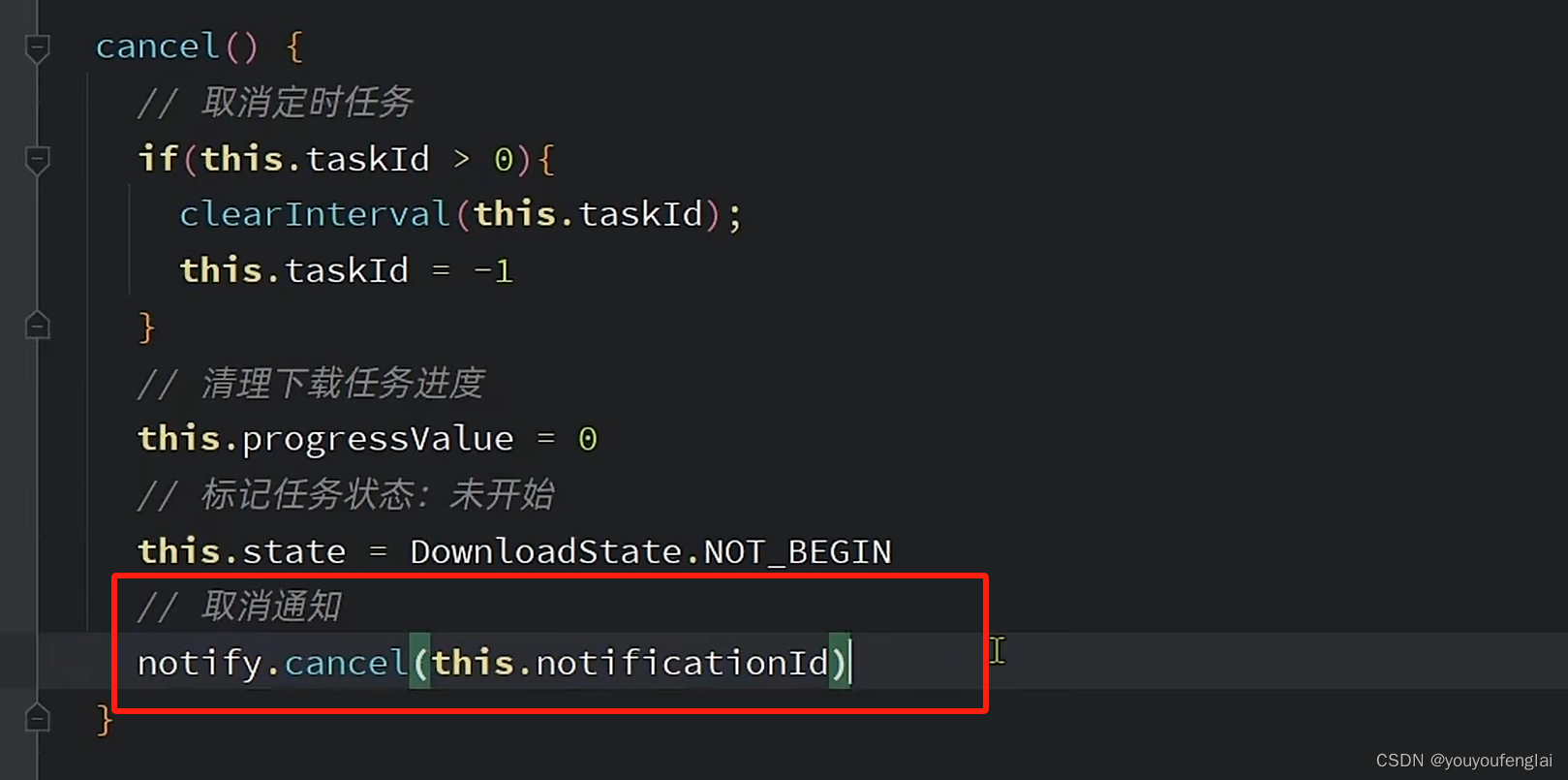
【HarmonyOS4学习笔记】《HarmonyOS4+NEXT星河版入门到企业级实战教程》课程学习笔记(二十三)
课程地址: 黑马程序员HarmonyOS4NEXT星河版入门到企业级实战教程,一套精通鸿蒙应用开发 (本篇笔记对应课程第 33 节) P33《32.通知-进度条通知》 下载按钮对应的逻辑: 取消按钮对应的逻辑: 暂停按钮对应的…...
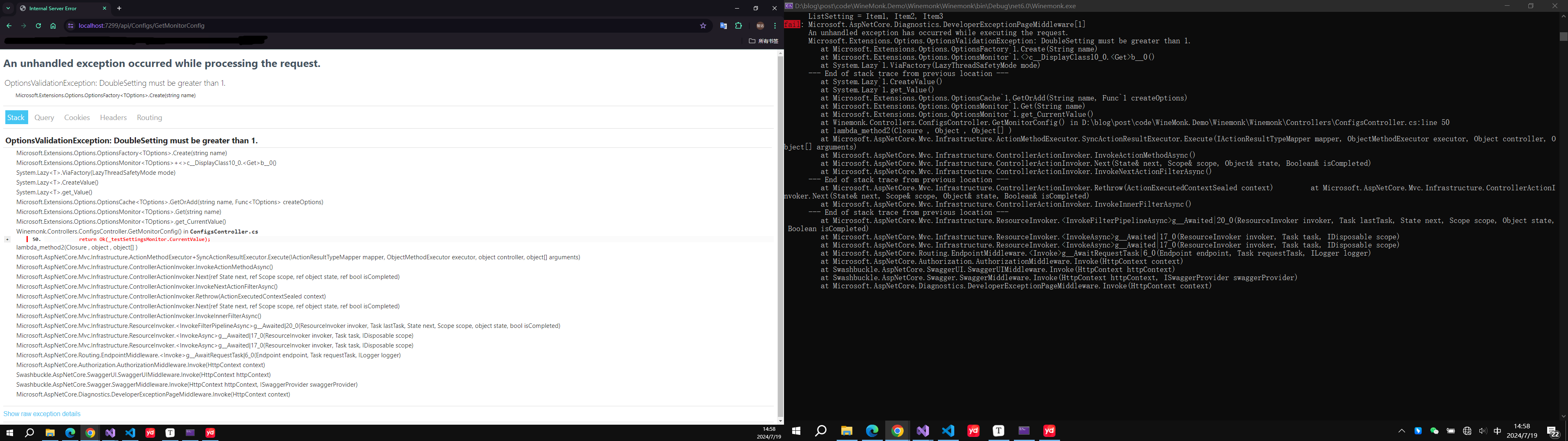
.NET C# 配置 Options
.NET C# 配置 Options 使用 options 模式可以带来许多好处,包括清晰的配置管理、类型安全、易于测试和灵活性。但在使用过程中,也需要注意配置复杂性、性能开销和依赖框架等问题。通过合理设计和使用,可以充分发挥 options 模式的优势&#…...

42、PHP 实现把二叉树打印成多行
题目: PHP 实现把二叉树打印成多行 描述: 从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。 <?php/*class TreeNode{var $val;var $left NULL;var $right NULL;function __construct($val){$this->val $val;} }…...

verilog bug记录——正点原子spi_drive存在的问题
verilog bug记录——正点原子spi_drive存在的问题 问题概述代码修改—spi_drive.v遗留问题 问题概述 因为项目需求,需要利用spi对flash进行擦除和写入操作,所使用的开发板是正电原子的达芬奇开发板,我事先往Flash里面存了两个bit,…...

vue+watermark-dom实现页面水印效果
前言 页面水印大家应该都不陌生,它可以用于验证数字媒体的来源和完整性,还可以用于版权保护和信息识别,这些信息可以在不影响媒体质量的情况下嵌入,并在需要时进行提取。本文将通过 vue 结合 watermark-dom 库,教大…...

为什么要学习网安技术?
学习网络安全(网安)技术在当今社会变得尤为重要,这主要源于以下几个方面的原因: 保护个人隐私:随着互联网的普及,个人信息如姓名、地址、电话号码、甚至银行账户信息等都在网络上留下了痕迹。学习网安技术可…...

2024春秋杯网络安全联赛夏季赛Crypto(AK)解题思路及用到的软件
2024春秋杯网络安全联赛夏季赛Crypto(AK) 2024春秋杯网络安全联赛夏季赛Crypto解题思路以及用到的软件 所有题用到的软件 1.vm(虚拟机kali)和Ubuntu,正常配置即可B站有很多。 2.Visual Studio Code(里面要配置python,crypto库和Sagemath数学软件系统S…...

vue2 使用代码编辑器插件 vue-codemirror
vue 使用代码编辑器插件 vue-codemirror 之前用过一次,当时用的一知半解的,所以也没有成文,前几天又因为项目有需求,所以说有用了一次,当然,依旧是一知半解,但是还是稍微写一下子吧!…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
