为什么 FPGA 的效率低于 ASIC？

FPGA是“可重构逻辑”器件。先制造的芯片，再次设计时“重新配置”。

ASIC 不需要“重新配置”。你先设计，把它交给代工厂，然后制造芯片。

现在让我们看看这些芯片的结构是什么样的，以及它们的不同之处。

● 逻辑单元：FPGA的基础模块

这是最小的逻辑块。LUT 充当组合逻辑。在DFF的帮助下，可以形成时序逻辑。

它可以构建逻辑门、多路复用器、编码器、加法器;任何真值表都可以作为布尔表达式存储在 LUT 中。

一个 LUT 可以保存有限数量的数据。逻辑单元的 LUT 也是有限的。

具有许多项的布尔表达式需要更多的内存空间，工具在布局布线的时候会将剩余项放入另一个逻辑单元中。这就需要在两个逻辑单元之间有路由信号。

● FPGA路由信号

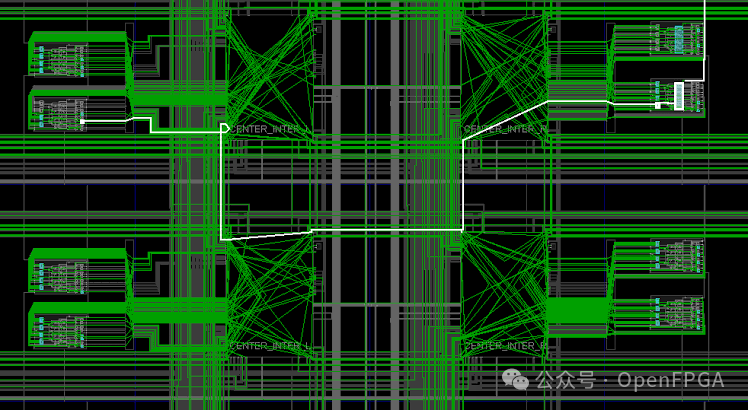
白线是从一个逻辑单元路由到另一个逻辑单元的信号。可以想象如果实现更大逻辑时候这个导线长度会增加多大。这增加了额外的延迟，降低了时钟频率，消耗了更多的面积和功耗。

所有这一切都只是为了“重构”。

即使设计不需要其他单元或路由信号，它们仍然存在于FPGA芯片路由区域和静态功率中，从而降低了效率。

● 标准单元：ASIC的构建模块

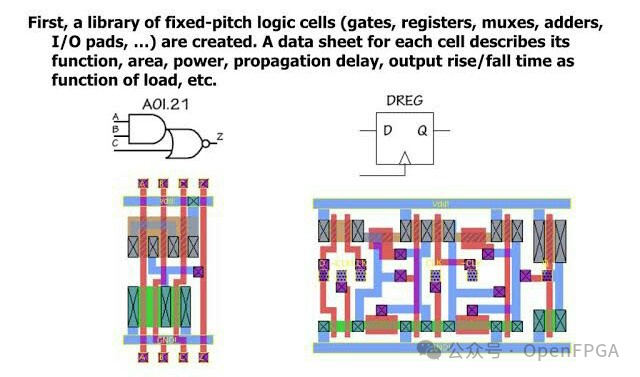
标准单元库可以具有小至 NAND 门的组件和 IP，例如加法器、FF、BRAM、多路复用器等。

所有标准单元库都针对面积和功率进行了优化。

● ASIC布局：

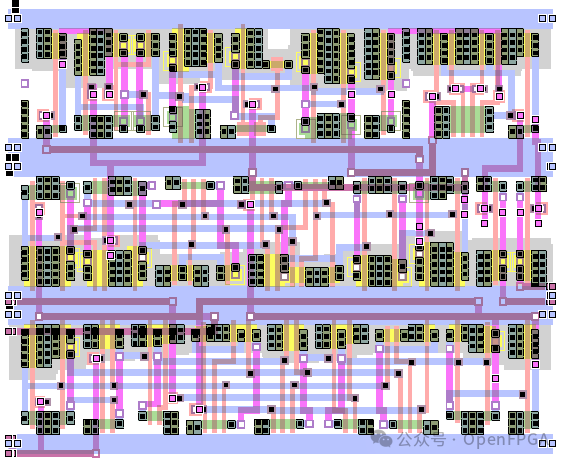
单个单元彼此紧密连接，形成更大的逻辑功能。位置也针对信号传播进行了优化。与FPGA相比，ASIC没有不必要的逻辑和路由开销。这样可以节省更少的面积和功率。还可以实现更快的时钟。

以上这些ASIC会比FPGA具有更高的效率。