有监督学习基础
基本概念
给定输入有为(x,y),其中x表示学习特征,y表示输出,m表示输入总数,有监督学习旨在根据输入建立能够预测可能输出的模型,大致可以分为回归和分类两种,代表可能输出是无限的或是有限可能。
模型
线性回归模型
通过数据集建立回归模型,表现形式为根据数据点建立曲线,如y~=wx+b,用于预测无限可能的数字。
分类模型
少量可能输出的预测,比如图片内容识别,音频字符识别等情况。
基本训练过程为
训练集—学习算法—预测方法
成本函数J
用于衡量建立曲线与数据点的差异大小,即曲线的拟合程度,通过平均误差成本函数实现—
除m是为了避免误差随着数据集增大而增大,而除2是为了后续化简,使程序整洁。
构建模型的目的是使成本函数J尽可能小,为了简化,暂时不考虑b。
梯度下降
找w和b使成本函数最小的方法,也是逐步确定拟合曲线的方法,将参数初始化为0,每次尝试使J减小的方向,可视化如下:

本质是通过切线找到三维图像的最低点,从任意点开始找w和b使成本函数最小的方法如式:


上述两个迭代公式需同步计算,上述步骤不断重复直到收敛,可以实现成本函数不断向局部最小值更新,其中a又称学习率,用于控制上下坡的步幅。
线性回归
用向量分别表示输入x和参数w,f(x)=w·x+b,特征多数据大时,传统计算方法耗时很长,故考虑采取其他技术解决。
矢量化
w=np.array([]),x=np.array([])生成向量,但计算时不使用循环乘法,二十直接调用f=np.dot(w,x)+b实现点积运算,该方法快于for循环,使用并行硬件,执行快。
梯度下降
w由原有计算式带入可得
相应的,b的新计算式为

这里求导平方的2就和成本函数J分母加的2抵消,使式子简洁。
另外还有法方程法可用,但该方法并不通用,只在这种场景下可以无需迭代求解w和b,但梯度下降是通用的方法。
特征缩放
单个特征对J的影响很大时,会导致曲线变化太大,梯度下降来回跳动,无法找到极值点,如下图

此时我们可以选择缩放特性,使整体的特征值大致在同一范围内,使用除法或平均归一化方法。
判断收敛
通过学习曲线检查梯度下降是否收敛,如下图

可以看出随着迭代次数的上升成本函数不断下降并趋于一个固定值,此时可以声明其收敛,但该方法的难度在于确定一个阈值。
选择学习率
太小则计算步骤增多,太大则可能跨过极值点,导致计算永远达不到最小值,需要尝试绘图找到合适的值,在接近最小值后由于偏导变化,步子会自动变小,同样需要尝试根据学习曲线图像选择。

如果学习曲线上下摆动,则可能是学习率的选择过于大了。
选择特征
可以根据需要创建新特性,如果曲线不能线性拟合,也可以使用特征多项式提高特征次数,获得拟合曲线,在该部分特征缩放显得尤其重要。
logistic回归
用于分类,拟合一条横S曲线,用于二进制的分类,具体公式如下,其中z=w·x+b,0<g(z)<1

图像大致如下:

该模型输出一个范围0-1的数字,代表分类为1的概率,多用于广告推荐算法,输出概率需设置阈值判定,常见的为0.5,该阈值称为决策边界,也就是z为0时的取值。
损失函数
单个点的损失L表示为:
L(z,y)= -log(z) y=1-log(1-z) y=0
具体含义为,当y=1,预测为真则无损,预测为0则损失极大,y=0相同,预测为1损失极大,预测为0无损,区间的损失用对数函数覆盖。
上述损失可以简化为:

当y=1或y=0时带入都可化简为初始式子。
总的损失函数J是所有点损失集合的平均数,表示为:

梯度下降


二者同样需要同时计算,与线性回归的区别只在f(x)上,一个是f=w·x+b,另一个是指数形式1/1+e^(w·x+b)。
其他
矢量化,特征缩放,判断收敛等,都与线性回归相同。
正则化
拟合与数据不匹配,称为偏差,拟合符合数据,但变化太多不能适应新数据,称为方差,或过拟合,如下三图分别表示偏差,合格拟合和方差。

解决过拟合的方法有:
1,收集更多数据,更大的训练集可以限制函数,拟合出摆动没那么大的图像
2,减少特征,数据不足但特征过多,易过拟合
3,减少参数大小,惩罚所有特征,可以使函数更平滑,表示公式如图:

其中lambda>0,使用正则化成本函数的思想为使w尽可能小。
正则化线性回归梯度下降
原有成本函数梯度下降为:


正则化logistic回归梯度下降


总结
本章学习了监督学习的两种算法,回归和分类,分别用于处理预测无限可能的数字,和有限输出的类型,本质都是通过对已有的数据建立拟合模型来实现,区别在于拟合曲线不同,拟合模型内部通过成本函数来衡量预测结果,每次模型调整又借助梯度下降实现,三者统一完成模型的建立与调整,最后,通过正则化来解决过拟合。
总结的总结,有监督学习的要点:标签、拟合曲线、成本函数、梯度下降、正则化,另外与无监督学习的区别就在于训练集有标签,在特定领域和指定情况效果佳。
另外,正则化之前的函数中分母m或2m应该提到最前并改为1/m,修改工作量大偷个小懒。
相关文章:

有监督学习基础
基本概念 给定输入有为(x,y),其中x表示学习特征,y表示输出,m表示输入总数,有监督学习旨在根据输入建立能够预测可能输出的模型,大致可以分为回归和分类两种,代表可能输出是无限的或…...

揭开 AI 绘画提示词的神秘密码!
前言 ** 揭秘AI 绘画 ** 提示词的神秘密码 亲爱的朋友们,今天我们要一起探索 AI 绘画世界中那神秘的“密码”——提示词。 在 AI 绘画的奇妙领域里,提示词就像是一把神奇的钥匙,能够开启无尽的创意之门。它是我们与 AI 进行心灵对话的桥…...

macOS 10.15中屏蔽Microsoft Edge浏览器的更新提示
文章目录 1.效果对比2.安装描述文件3.停用描述文件4.高级操作(可选)参考文献 最近在macOS10.15系统,打开Microsoft Edge浏览器,每次打开都有个烦人的提示“ 要获取将来的 microsoft edge 更新,需要 macos 10.15 或更高…...
数据类型 | 3.2、QVariant)
Qt 实战(3)数据类型 | 3.2、QVariant
文章目录 一、QVariant1、存储数据1.1、存储Qt内置数据1.2、存储自定义数据 2、获取数据3、判断数据类型4、清空数据5、总结 前言: QVariant是Qt框架中一个非常强大且灵活的类,它提供了一种通用的方式来存储和转换几乎任何类型的数据。无论是基本数据类型…...

Docker中安装的postgresql14在启用vector扩展的时候,找不到该扩展的控制文件。
ERROR: could not open extension control file “/usr/share/postgresql/14/extension/vector.control”: No such file or directory 进入容器 docker exec -it CONTAINER ID /bin/bash 1.更新 apt-get apt-get update 2.安装插件 #不同版本对应修改数字即可 apt-get i…...

JS防抖和节流
一、防抖和节流的适用场景 防抖(Debounce): 适合在输入框输入时的实时搜索、窗口大小调整时的resize事件等。节流(Throttle): 适合如页面滚动时的scroll事件、按钮点击时的请求发送等需要控制频率的场景。 …...

OpenWrt 为软件包和docker空间扩容
参考资料 【openwrt折腾日记】解决openwrt固件刷入后磁盘空间默认小的问题,关联openwrt磁盘扩容空间扩容【openwrt分区扩容】轻松解决空间可用不足的尴尬丨老李一瓶奶油的YouTube 划分空间 参考一瓶奶油的YouTube 系统 -> 磁盘管理 -> 磁盘 -> 修改 格…...
重要的工作任务,怎么在电脑桌面设置倒计时?
在日常工作中,我们总是面临着众多工作任务,如何高效地管理和完成这些任务成为了每个职场人的必备技能。为任务设置倒计时,不仅能让我们清晰地看到任务的先后顺序,还能帮助我们更好地把握时间,提高工作效率。想象一下&a…...

Failed to build get_cli:get:的解决方案
项目场景: 今天安装Getx命令行的时候,输入这面文档报了一个错: dart pub global activate get_cli 问题描述 提示:这里描述项目中遇到的问题: 例如:数据传输过程中数据不时出现丢失的情况,偶尔…...

短视频矩阵源码技术分享
在当今数字媒体时代,短视频已成为吸引观众和传递信息的重要手段。对于开发者而言,掌握短视频矩阵源码技术不仅是提升自身技能的需要,更是把握行业发展趋势的必然选择。本文将深入探讨短视频矩阵源码的关键技术要点及其实现方法,帮…...

轮播图自定义内容
官网:Swiper演示 - Swiper中文网 下载: npm i swiper Vue3示例代码: <template><div class"swiper mySwiper"><div class"swiper-wrapper"><div class"swiper-slide"><div>…...

大数据-44 Redis 慢查询日志 监视器 慢查询测试学习
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...
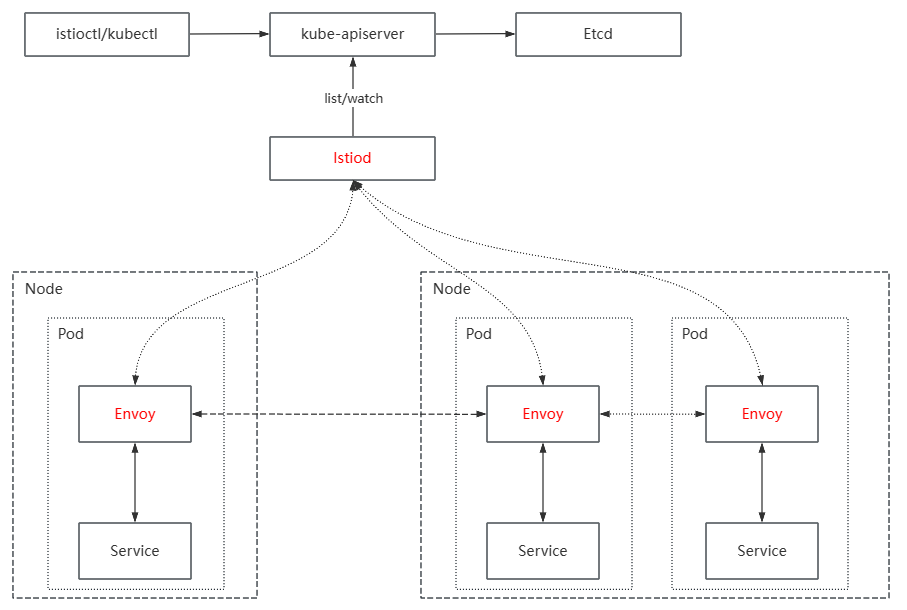
Istio_01_Istio初识
文章目录 IstioService Mesh Istio Istio: 以服务网格形态用于服务治理的开放平台和基础设施 本质: 以非侵入式治理服务之间的访问和调用服务治理: 流量管理、可观测性、安全性可同时管理多类基础设施(多种网络方案) 如: Istio和Kubernetes架构的结合 Istio通过Kubernetes的域…...

leetcode日记(47)螺旋矩阵Ⅱ
这题思路不难,就是找规律太难了。 我首先的思路是一行一行来,根据规律填入下一行的数组,第i行是由前i个数字(n-2*i)个增序数列后i个数字组成,后来觉得太难找规律了就换了一种思路。 思路大致是先计算出需…...

centos系统mysql主从复制(一主一从)
文章目录 mysql80主从复制(一主一从)一、环境二、服务器master1操作1.开启二进制日志2. 创建复制用户3. 服务器 slave1操作4. 在主数据库中添加数据 mysql80主从复制(一主一从) 一、环境 准备两台服务器,都进行以下操…...

IEDA怎么把springboot项目 启动多个
利用Idea提供的Edit Configurations配置应用参数。 点击Modify Options进行添加应用参数: 确保这里勾选...

Vue 3项目安装Element-Plus
Element Plus 是一个基于 Vue 3 的现代前端UI框架,它旨在提升开发体验,并为开发者提供高效、优雅的组件。如果你正在使用 Vue 3 进行项目开发,那么安装和集成 Element Plus 是一个不错的选择。在本文中,博主将详细介绍如何在 Vue …...

Git下载安装
一、介绍 Git是一个分布式版本控制系统,最初由Linus Torvalds创建,用于管理和跟踪代码的变化。它可以轻松地处理个人项目和大型团队项目的版本控制需求。 Git的主要特点包括: 分布式:每个开发者都可以拥有自己的本地仓库&#x…...

linux中的目录操作函数
参考 【Linux系统编程】Linux 文件系统探究:深入理解 struct dirent、DIR 和 struct stat结构 stat函数 C标准库提供了访问linux的目录的函数接口现对目录的操作。 一、libc接口 libc访问目录的流程为:打开目录,访问目录,关闭目…...

JSON 文件第一段飘红
问题 原因 这个问题通常发生在尝试用 ESLint 去解析 JSON 文件时。ESLint 主要设计用于检查 JavaScript 代码的语法和风格,而JSON是一种数据交换格式,不包含 JavaScript 的逻辑结构,如函数、变量声明等。 解释报错原因 当ESLint遇到它不能识…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
