Pytorch使用教学7-张量的广播

PyTorch中的张量具有和NumPy相同的广播特性,允许不同形状的张量之间进行计算。
广播的实质特性,其实是低维向量映射到高维之后,相同位置再进行相加。我们重点要学会的就是低维向量如何向高维向量进行映射。
相同形状的张量计算
虽然我们觉得不同形状之间的张量计算才是广播,但其实相同形状的张量计算本质上也是广播。
t1 = torch.arange(3)
t1
# tensor([0, 1, 2])# 对应位置元素相加
t1 + t1
# tensor([0, 2, 4])
与Python对比
如果两个list相加,结果是什么?
a = [0, 1, 2]
a + a
# [0, 1, 2, 0, 1, 2]
不同形状的张量计算
广播的特性是不同形状的张量进行计算时,一个或多个张量通过隐式转化成相同形状的两个张量,从而完成计算。
但并非任意两个不同形状的张量都能进行广播,因此我们要掌握广播隐式转化的核心依据。
2.1 标量和任意形状的张量
标量(零维张量)可以和任意形状的张量进行计算,计算过程就是标量和张量的每一个元素进行计算。
# 标量与一维向量
t1 = torch.arange(3)
# tensor([0, 1, 2])t1 + 1 # 等效于t1 + torch.tensor(1)
# tensor([1, 2, 3])
# 标量与二维向量
t2 = torch.zeros((3, 4))
t2 + 1 # 等效于t2 + torch.tensor(1)
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
2.2 相同维度,不同形状张量之间的计算
我们以t2为例来探讨相同维度、不同形状的张量之间的广播规则。
t2 = torch.zeros(3, 4)
t2
# tensor([[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]])t21 = torch.ones(1, 4)
t21
# tensor([[1., 1., 1., 1.]])
它们都是二维矩阵,t21的形状是1×4,t2的形状是3×4,它们在第一个分量上取值不同,但该分量上t21取值为1,因此可以进行广播计算:
t2 + t21
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
而t2和t21的实际计算过程如下:

可理解为t21的一行与t2的三行分别进行了相加。而底层原理为t21的形状由1×4拓展成了t2的3×4,然后二者对应位置进行了相加。
t22 = torch.ones(3, 1)
t22
# tensor([[1.],
# [1.],
# [1.]])t2 + t22
# tensor([[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]])
同理,t22+t2与t21+t2结果相同。如果矩阵的两个维度都不相同呢?
t23 = torch.arange(3).reshape(3, 1)
t23
# tensor([[0],
# [1],
# [2]])t24 = torch.arange(3).reshape(1, 3)
# tensor([[0, 1, 2]])t23 + t24
# tensor([[0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])
此时,t23的形状是3×1,而t24的形状是1×3,二者的形状在两个份量上均不同,但都有1存在,因此可以广播:

如果两个张量的维度对应数不同且都不为1,那么就无法广播。
t25 = torch.ones(2, 4)
# t2的shape为3×4
t2 + t25
# RuntimeError
高维张量的广播
高维张量的广播原理与低维张量的广播原理一致:
t3 = torch.zeros(2, 3, 4)
t3
# tensor([[[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]],# [[0., 0., 0., 0.],
# [0., 0., 0., 0.],
# [0., 0., 0., 0.]]])t31 = torch.ones(2, 3, 1)
t31
# tensor([[[1.],
# [1.],
# [1.]],# [[1.],
# [1.],
# [1.]]])t3+t31
# tensor([[[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]],# [[1., 1., 1., 1.],
# [1., 1., 1., 1.],
# [1., 1., 1., 1.]]])
总结
维度相同时,如果对应分量不同,但有一个为1,就可以广播。
不同维度计算中的广播
对于不同维度的张量,我们首先可以将低维的张量升维,然后依据相同维度不同形状的张量广播规则进行广播。
低维向量的升维也非常简单,只需将更高维度方向的形状填充为1即可:
# 创建一个二维向量
t2 = torch.arange(4).reshape(2, 2)
t2
# tensor([[0, 1],
# [2, 3]])# 创建一个三维向量
t3 = torch.zeros(3, 2, 2)
t3t2 + t3
# tensor([[[0., 1.],
# [2., 3.]],# [[0., 1.],
# [2., 3.]],# [[0., 1.],
# [2., 3.]]])
t3和t2的相加,就相当于1×2×2和3×2×2的两个张量进行计算,广播规则与低维张量一致。
相信看完本节,你已经充分掌握了广播机制的运算规则:
- 维度相同时,如果对应分量不同,但有一个为1,就可以广播
- 维度不同时,只需将低维向量的更高维度方向的形状填充为1即可
Pytorch张量操作大全:
Pytorch使用教学1-Tensor的创建
Pytorch使用教学2-Tensor的维度
Pytorch使用教学3-特殊张量的创建与类型转化
Pytorch使用教学4-张量的索引
Pytorch使用教学5-视图view与reshape的区别
Pytorch使用教学6-张量的分割与合并
Pytorch使用教学7-张量的广播
Pytorch使用教学8-张量的科学运算
Pytorch使用教学9-张量的线性代数运算
Pytorch使用教学10-张量操作方法大总结

相关文章:

Pytorch使用教学7-张量的广播
PyTorch中的张量具有和NumPy相同的广播特性,允许不同形状的张量之间进行计算。 广播的实质特性,其实是低维向量映射到高维之后,相同位置再进行相加。我们重点要学会的就是低维向量如何向高维向量进行映射。 相同形状的张量计算 虽然我们觉…...

生成式AI:对话系统(Chat)与自主代理(Agent)的和谐共舞
生成式AI:对话与行动的和谐共舞 我们正站在一个令人激动的时代门槛上——生成式AI技术飞速发展,带来了无限的可能性。一个关键问题浮现:AI的未来是对话系统(Chat)的天下,还是自主代理(Agent&am…...
唯众物联网(IOT)全功能综合实训教学解决方案
一、引言 在信息技术日新月异的今天,物联网(IoT)作为推动数字化转型的关键力量,其触角已延伸至我们生活的方方面面,深刻地重塑了工作模式、生活习惯乃至社会结构的每一个角落。面对这一前所未有的变革浪潮,…...

24证券从业考试报名『个人信息表』填写模板❗
24证券从业考试报名『个人信息表』填写模板❗ 1️⃣居住城市、通讯地址:写自己现居住的地址就可以。 2️⃣学历:需要注意的是学历填写的是考生已经取得的学历,在校大学生已经不具有报名资格,选择大专以上,或者是高中学…...

深度学习系列70:模型部署torchserve
1. 流程说明 ts文件夹下, 从launcher.py进入,执行jar文件。 入口为model_server.py的start()函数。内容包含: 读取args,创建pid文件 找到java,启动model-server.jar程序,同时读取log-config文件ÿ…...
算法日记day 20(中序后序遍历序列构造二叉树|最大、合并、搜索二叉树)
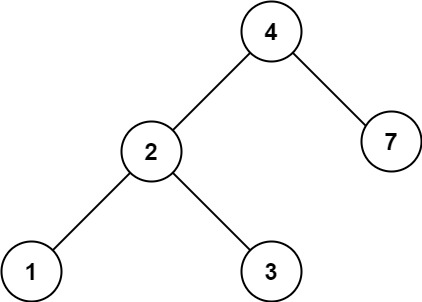
一、中序后序序列构造二叉树 题目: 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,…...

【科研】# Taylor Francis 论文 LaTeX template模版 及 Word模版
【科研写论文】系列 文章目录 【科研写论文】系列前言一、Word 模板(附下载网址):二、LaTeX 版本方法1:直接网页端打开(附网址)方法2:直接下载到本地电脑上编辑下载地址说明及注意事项 前言 给…...

Linux网络配置及常见命令!
vim /etc/sysconfig/network-scripsts/ifcfg-ens33(图形界面配置网络) Xshell rz:上传(从Windows到Linux) sz:下载:(从Linux到Windows)(后接文件手工输入)…...

linux之shell脚本实战
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:Linux运维老纪的首页…...

文件上传漏洞(ctfshow web151-161)
Web151 F12修改源代码 exts后面png改为php 这样就可以上传php的文件了 Web152: 考点:后端不能单一校验 就是要传图片格式,抓个包传个png的图片 然后bp抓包修改php后缀解析 然后放包 Web153-web156 在php代码中可以使用“{}”代替“[]” …...

小猪佩奇.js
闲着没事 使用js 画一个小猪佩奇把 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</tit…...
人工智能AI合集:Ollama部署对话语言大模型-网页访问
目录 🍅点击这里查看所有博文 随着人工智能技术的飞速发展,AI已经不再是遥不可及的高科技概念,而是逐渐融入到我们的日常生活中。从智能手机的语音助手到家庭中的智能音箱,再到工业自动化和医疗诊断,AI的应用无处不在…...

CentOS搭建Apache服务器
安装对应的软件包 [roothds ~]# yum install httpd mod_ssl -y 查看防火墙的状态和selinux [roothds ~]# systemctl status firewalld [roothds ~]# cat /etc/selinux/config 若未关闭,则关闭防火墙和selinux [roothds ~]# systemctl stop firewalld [roothds ~]# …...

CDGA|数据治理:安全如何贯穿数据供给、流通、使用全过程
随着信息技术的飞速发展,数据已经成为企业运营、社会管理和经济发展的核心要素。然而,数据在带来巨大价值的同时,也伴随着诸多安全风险。因此,数据治理的重要性日益凸显,它不仅仅是对数据的简单管理,更是确…...

32单片机bootloader程序
一,单片机为什么要使用bootloader 1、使用bootloader的好处 1) 程序隔离:可以同时存在多个程序,只要flash空间够大,或者通过外挂flash,可以实现多个程序共存,在多个程序之间切换使用。 2)方便程…...

MongoDB - 数组更新操作符:$、$[]、$pop、$pull、$push、$each、$sort、$slice、$position
文章目录 1. $1. 更新数组中的值2. 更新数组中的嵌入文档 2. $[]1. 更新数组中的所有元素2. 更新数组中的所有嵌入文档 3. $pop1. 删除数组的第一个元素2. 删除数组的最后一个元素 4. $pull1. 删除所有等于指定值的项2. 删除与指定条件匹配的所有项3. 从文档数组中删除项4. 从嵌…...

多GPU并行处理[任务分配、进程调度、资源管理、负载均衡]
1. 多GPU并行处理设计 设计思路: 实现基于多GPU的并行任务处理,每个GPU运行独立的任务,以加速整体的处理速度。 实现机制: 进程隔离: 利用multiprocessing.Process为每个GPU创建独立的工作进程。 GPU资源限制: 通过设置CUDA_VISIBLE_DEVICES环境变量&…...

项目部署到服务器
(相关资源都给出来了) 1 下载MobaXterm,然后打开 正常连接输入你的服务器IP,用户名可以起名为root 2 将JDK,Tomcat,mysql安装包 布置到服务器中(JDK官网地址:https://www.oracle.com/java/technologies/downloads/#java8 mysql官网地址: …...

Idea2024 创建Meaven项目没有src文件夹
1、直接创建 新建maven项目,发现没有src/main/java 直接新建文件夹:右击项目名->new->Directory 可以看到idea给出了快捷创建文件夹的选项,可以根据需要创建,这里点击src/main/java 回车,可以看到文件夹已经创建…...

LeetCode 2766.重新放置石块:哈希表
【LetMeFly】2766.重新放置石块:哈希表 力扣题目链接:https://leetcode.cn/problems/relocate-marbles/ 给你一个下标从 0 开始的整数数组 nums ,表示一些石块的初始位置。再给你两个长度 相等 下标从 0 开始的整数数组 moveFrom 和 moveTo…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
