【数据结构】二叉树链式结构——感受递归的暴力美学
前言:
在上篇文章【数据结构】二叉树——顺序结构——堆及其实现中,实现了二叉树的顺序结构,使用堆来实现了二叉树这样一个数据结构;现在就来实现而二叉树的链式结构。
一、链式结构
链式结构,使用链表来表示一颗二叉树,即用链来指示二叉树中元素的逻辑关系。通常的就是链表中每个节点右三个域组成,数据域和左右指针域,左右指针分别指向该节点的左孩子节点和右孩子节点的存储地址。
链式结构分为二叉链和三叉链(三叉链比而二叉链多一个指向父节点的指针域)。

这里使用二叉链来实现。
二、二叉树链式结构实现相关功能
在实现之前,先来看一下,具体要实现哪些功能?
首先就是二叉树的结构,我们使用链表来实现,链表的每一个节点都由数值域和左右指针域组成。
二叉树链式结构的节点
typedef int TreeDataType;
typedef struct TreeNode
{TreeDataType data;struct TreeNode* left;struct TreeNode* right;
}TreeNode;
二叉树链式结构如上,接下来再来看一下二叉树链式结构实现的相关功能:
//二叉树的前序排序
int PreOrder(TreeNode* root);
//二叉树的中序排序
int InOrder(TreeNode* root);
//二叉树的后序遍历
int AfterOrter(TreeNode* root);
//二叉树节点个数
int BinaryTreeSize(TreeNode* root);
//二叉树叶子节点个数
int BinaryTreeLeafSize(TreeNode* root);
//二叉树第k层节点个数
int BinaryTreeLevelKSize(TreeNode* root, int k);
//二叉树的深度
int BinaryTreeDepth(TreeNode* root);
//查找二叉树值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, TreeDataType x);
//层序遍历
void LevelOrder(BTNode* root)
//判断是否为满二叉树
bool BinaryTreeComplete(BTNode* root)
//二叉树的销毁
void TreeDesTroy(TreeNode** root);2.1、二叉树前、中、后序遍历
这里,前序、中序和后序遍历什么意思呢,

说白了,这三种遍历其实就是以对二叉树访问的顺序,来遍历二叉树
这里以前序遍历为例,遍历二叉树

现在有一个这样的二叉树,用前序遍历来访问这颗二叉树(这里访问并输出访问到的数据)

首先访问根节点,输出访问到的数据 1 ;再访问左子树

再访问其左子树的根节点,输出访问到的数据 2 ;再接着访问左子树

再访问其左子树的根节点,输出访问到的数据 4 ;再接着访问左子树

此时访问到了空节点,就直接回退,回退到其父节点的函数栈帧,访问父节点的右子树

访问4这个节点的右子树,也为空,此时节4这个点为根节点的左子树已经访问 结束了,回退到其父节点的函数栈帧,访问其父节点的右子树

访问2这个节点的右子树,先输出右子树的根节点数据 5 ;再访问根节点5的左子树

这里节点5的左右节点都为空,这里省略一些过程;此时5这个节点访问结束,回退到2这个节点,而2这个节点右子树访问结束,也已经访问结束了;此时再回退到根节点,访问根节点的右子树。

此时访问根节点的右子树的根节点,输出访问到的数据 3 ;再接着访问3这个节点的左子树

这里,3这个节点的左右节点都为空,访问就直接返回,回退到根节点,就说明根节点的右子树访问已经结束,此时二叉树已经变了结束。
这里前序遍历的输出结果为 1 2 4 5 3
这三个前、中、后序遍历本质上没啥差别,这里直接看实现代码
//二叉树的前序排序
void PreOrder(TreeNode* root)
{if (root == NULL){return;}//输出数据printf("%d ", root->data);//遍历左子树PreOrder(root->left);//遍历右子树PreOrder(root->right);
}
//二叉树的中序排序
void InOrder(TreeNode* root)
{if (root == NULL){return;}//遍历左子树InOrder(root->left);//输出数据printf("%d ", root->data);//遍历右子树InOrder(root->right);
}
//二叉树的后序遍历
void AfterOrter(TreeNode* root)
{if (root == NULL){return;}//遍历左子树AfterOrter(root->left);//遍历右子树AfterOrter(root->right);//输出数据printf("%d ", root->data);
}这里我们来测试代码对不对,我们先创建一个二叉树,然后看输出结果是否正确、
TreeNode* BuyNode(TreeDataType x)
{TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));if (newnode == NULL){perror("malloc");exit(1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}void test()
{TreeNode* node1 = BuyNode(1);TreeNode* node2 = BuyNode(2);TreeNode* node3 = BuyNode(3);TreeNode* node4 = BuyNode(4);TreeNode* node5 = BuyNode(5);node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;//前序遍历PreOrder(node1);printf("\n");//中序遍历InOrder(node1);printf("\n");//后序遍历AfterOrter(node1);printf("\n");
}
int main()
{test();return 0;
}
这里代码没有问题。
2.2、二叉树节点个数
这里,二叉树的链式结构我们是使用递归来实现的,那我们该如何去计算二叉树的节点个数呢?
思路:
遍历二叉树,遍历到空节点就返回0,不是空节点就返回其左子树和右子树节点个数之和再加一
代码如下:
//二叉树节点个数
int BinaryTreeSize(TreeNode* root)
{if (root == NULL){return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}2.3、二叉树叶子结点个数
所谓叶子节点:就是左右子节点都为空的节点,我们就利用这个特点来判断
思路:
遍历二叉树,遍历到空节点就返回空;遍历到节点的左右节点都为空,返回1;否则就返回节点的左子树和右子树的叶子结点之和。
代码如下:
//二叉树叶子节点个数
int BinaryTreeLeafSize(TreeNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}2.4、二叉树第k层节点个数
求二叉树第k层节点的个数,我们先来看这样的一个图

通过图我们可以看到,每次向下遍历一层,k-1;当k=1时,正好是第k层
思路:
遍历二叉树,遍历到空节点就返回 0 ;遍历到k=1时,就返回1;否则就返回该节点左子树和右子树中第k - 1层的节点个数。
这里需要注意,要在判断k=1之前判断节点是否为空。
代码如下:
//二叉树第k层节点个数
int BinaryTreeLevelKSize(TreeNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}2.5、二叉树的深度
求二叉树的深度,我们这里是将二叉树的左子树和右子树分开依次遍历的,显然我们不能像上面一样,返回遍历左子树和右子树的和;这里就返回其中最大的。
思路:
遍历二叉树,遍历到空节点就返回空;定义两个值,记录其节点左子树和右子树的深度再加一;返回其中最大的即可。
理解:这里定义两个值记录其左右子树的深度加一(加一就是记录当前这一层)。
代码如下:
//二叉树的深度
int BinaryTreeDepth(TreeNode* root)
{if (root == NULL){return 0;}int depth_left = BinaryTreeDepth(root->left) + 1;int depth_right = BinaryTreeDepth(root->right) + 1;return (depth_left > depth_right) ? depth_left : depth_right;
}2.6、查找二叉树中值为 x 的节点
查找相对来说就比较简单了,遍历二叉树,为空就返回NULL,值为x就返回该节点的地址,如果遍历过程中函数返回值不为NULL,就证明找到了,直接返回即可。
思路:
遍历二叉树,遍历到空节点就返回NULL;判断节点的值是否为x,是就返回该节点的地址;不是。就创建指针变量接受其左右子树遍历的结果,如果不为NULL就直接返回该返回值。为空则继续遍历。
代码如下:
//查找二叉树值为x的节点
TreeNode* BinaryTreeFind(TreeNode* root, TreeDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}TreeNode* pleft = BinaryTreeFind(root->left, x);if (pleft)return pleft;TreeNode* pright = BinaryTreeFind(root->right, x);if (pright)return pright;return NULL;
}到这里,来看一下这些代码是否正确

 对于这样的一个二叉树,代码输出结果都正确。
对于这样的一个二叉树,代码输出结果都正确。
2.7、层序遍历
这里层序遍历,我们需要借用队列这样一个数据结构(前面有详细讲解),
大致思路如此:

将根节点数据放入队列中;然后出队列,并且把该节点的左右子节点插入到队列当中。

将1这个节点出队列,再把左右子节点插入到队列当中

再出队头节点,将其左右子节点插入队列当中

依次类推,当队头数据左右子节点为空,就不进插入队列这一操作。

代码如下:
这里用到了对列相关代码,详细代码在上篇
//层序遍历
//借助数据结构---队列
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){//取队头,打印BTNode* front = QueueFront(&q);printf("%d ", front->data);QueuePop(&q);//队头节点的左右孩子入队列if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}//队列为空QueueDestroy(&q);
}2.8、判断二叉树是否为满二叉树
判断二叉树是否为满二叉树,还是借用队列这样的数据结构,和层序遍历有相似之处;与层序遍历不同的是,这里,即便左右子节点为空,有进行入队列操作;当队头数据为空,就判断队列剩余数据是否都为空,如果都为空,就证明二叉树为满二叉树;否则就不是满二叉树。
代码如下:
//判断二叉树是否为完全二叉树
//---队列
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//队列不一定为空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}2.9、二叉树的销毁
这里为了测试这些代码,就手动创建了一个二叉树,这些都是动态开辟的空间,养成好习惯,手动释放动态开辟的空间。
这里需要注意的是:使用后序遍历,先是否底层的节点,
代码如下:
// 二叉树销毁
void BinaryTreeDesTroy(TreeNode** root)
{if (*root == NULL){return;}BinaryTreeDesTroy(&((*root)->left));BinaryTreeDesTroy(&((*root)->right));free(*root);*root = NULL;
}感谢各位大佬支持并指出问题,
如果本篇内容对你有帮助,可以一键三连支持以下,感谢支持!!!

相关文章:

【数据结构】二叉树链式结构——感受递归的暴力美学
前言: 在上篇文章【数据结构】二叉树——顺序结构——堆及其实现中,实现了二叉树的顺序结构,使用堆来实现了二叉树这样一个数据结构;现在就来实现而二叉树的链式结构。 一、链式结构 链式结构,使用链表来表示一颗二叉树…...
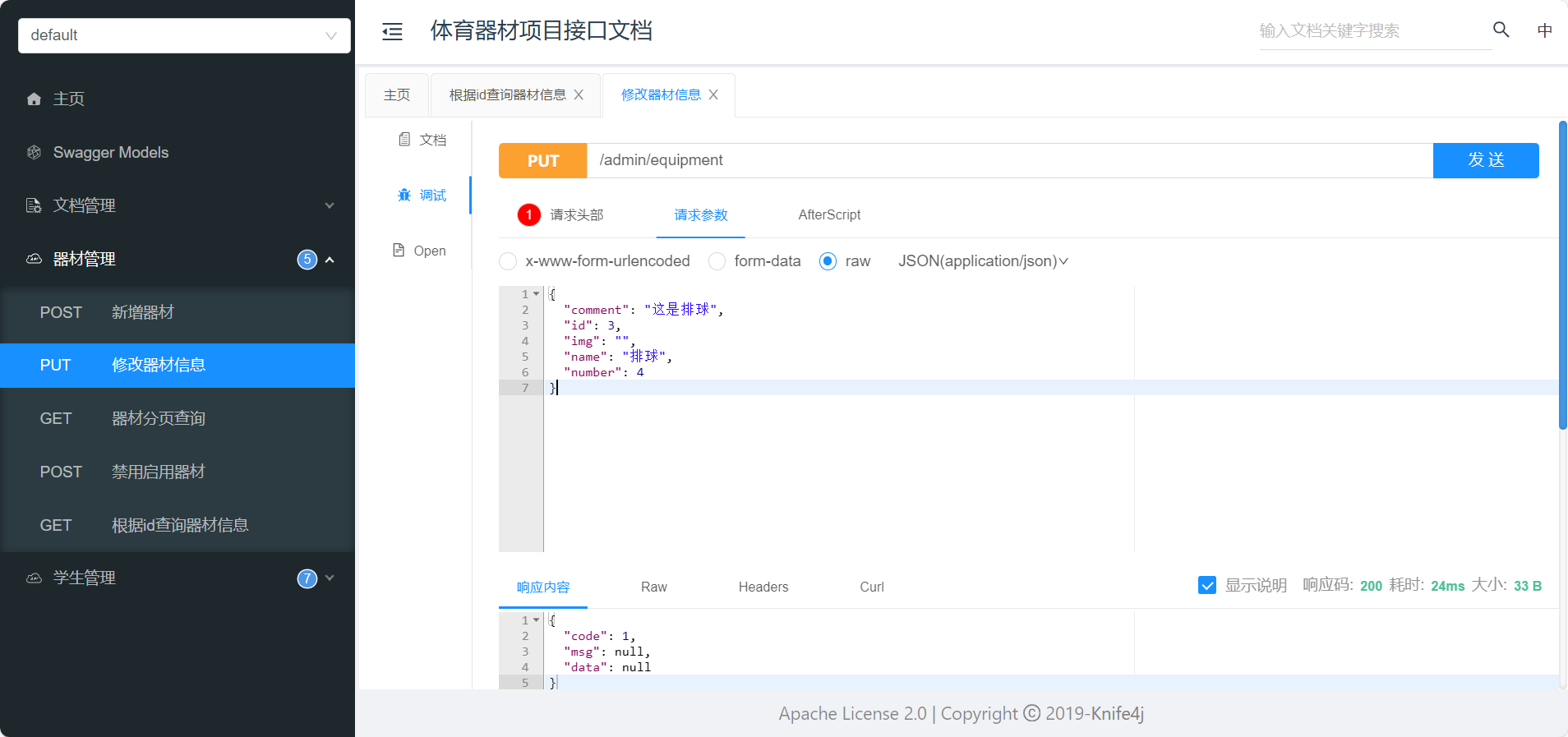
开始尝试从0写一个项目--后端(三)
器材管理 和员工管理基本一致,就不赘述,展示代码为主 新增器材 表设计: 字段名 数据类型 说明 备注 id bigint 主键 自增 name varchar(32) 器材名字 img varchar(255) 图片 number BIGINT 器材数量 comment VARC…...

2024年7月解决Docker拉取镜像失败的实用方案,亲测有效
在Ubuntu 16.04、Debian 8、CentOS 7系统中,若遇到Docker拉取镜像失败的问题,以下是一些亲测有效的解决方案: 配置加速地址 首先,创建Docker配置目录:sudo mkdir -p /etc/docker然后,编辑daemon.json文件…...

基于内容的音乐推荐网站/基于ssm的音乐推荐系统/基于协同过滤推荐的音乐网站/基于vue的音乐平台
获取源码联系方式请查看文末🍅 摘 要 随着信息化时代的到来,系统管理都趋向于智能化、系统化,音乐推荐网站也不例外,但目前国内的有些公司仍然都使用人工管理,公司规模越来越大,同时信息量也越来越庞大&…...

STM32智能工业监控系统教程
目录 引言环境准备智能工业监控系统基础代码实现:实现智能工业监控系统 4.1 数据采集模块 4.2 数据处理与控制模块 4.3 通信与网络系统实现 4.4 用户界面与数据可视化应用场景:工业监控与优化问题解决方案与优化收尾与总结 1. 引言 智能工业监控系统通…...
)
WEB渗透Web突破篇-SQL注入(MYSQL)
注释符 # -- 注意这里有个空格 /* hello */ /*! hello */ /*!32302 10*/ MYSQL version 3.23.02联合查询 得到列数 order by或group by 不断增加数字,直到得到报错响应 1 ORDER BY 1-- #True 1 ORDER BY 2-- #True 1 ORDER BY 3-- #True 1 ORDER BY 4-- #Fal…...
PDF解锁网站
https://smallpdf.com/cn/unlock-pdfhttps://smallpdf.com/cn/unlock-pdfhttps://www.freemypdf.comhttps://www.freemypdf.com...
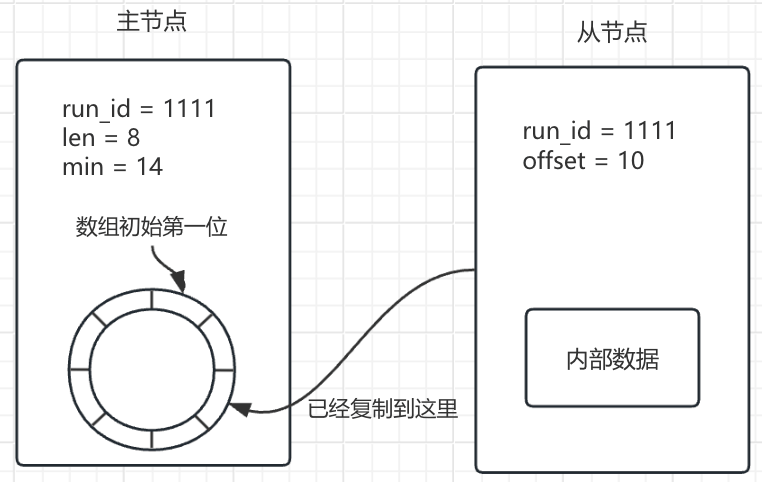
【Redis】主从复制分析-基础
1 主从节点运行数据的存储 在主从复制中, 对于主节点, 从节点就是自身的一个客户端, 所以和普通的客户端一样, 会被组织为一个 client 的结构体。 typedef struct client {// 省略 } client;同时无论是从节点, 还是主节点, 在运行中的数据都存放在一个 redisServer 的结构体中…...

Transformer自然语言处理实战pdf阅读
一.第一章 欢迎来到transformer的世界 1.解码器-编码器框架 在Transformer出现之前,NLP的最新技术是LSTM等循环架构。这些架 构通过在神经网络连接使用反馈循环,允许信息从一步传播到另一 步,使其成为对文本等序列数据进行建模的理想选择。如…...
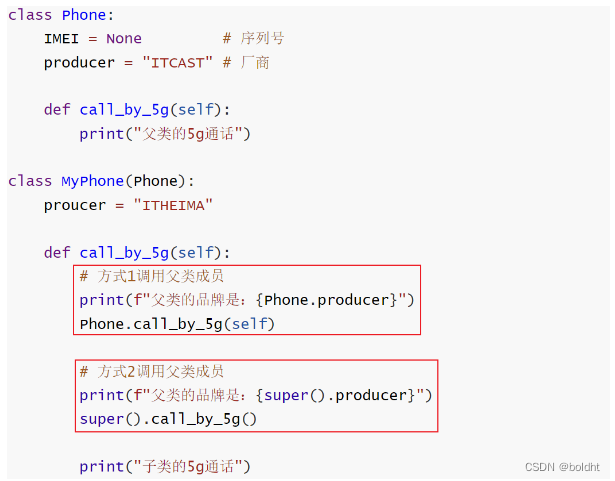
Python 高阶语法
前言: 我们通过上篇文章学习了Python的基础语法,接下来我们来学习Python的高阶语法 1.初识对象 在Python中我们可以做到和生活中那样,设计表格、生产表格、填写表格的组织形式的 面向对象包含 3 大主要特性: 封装 继承 …...
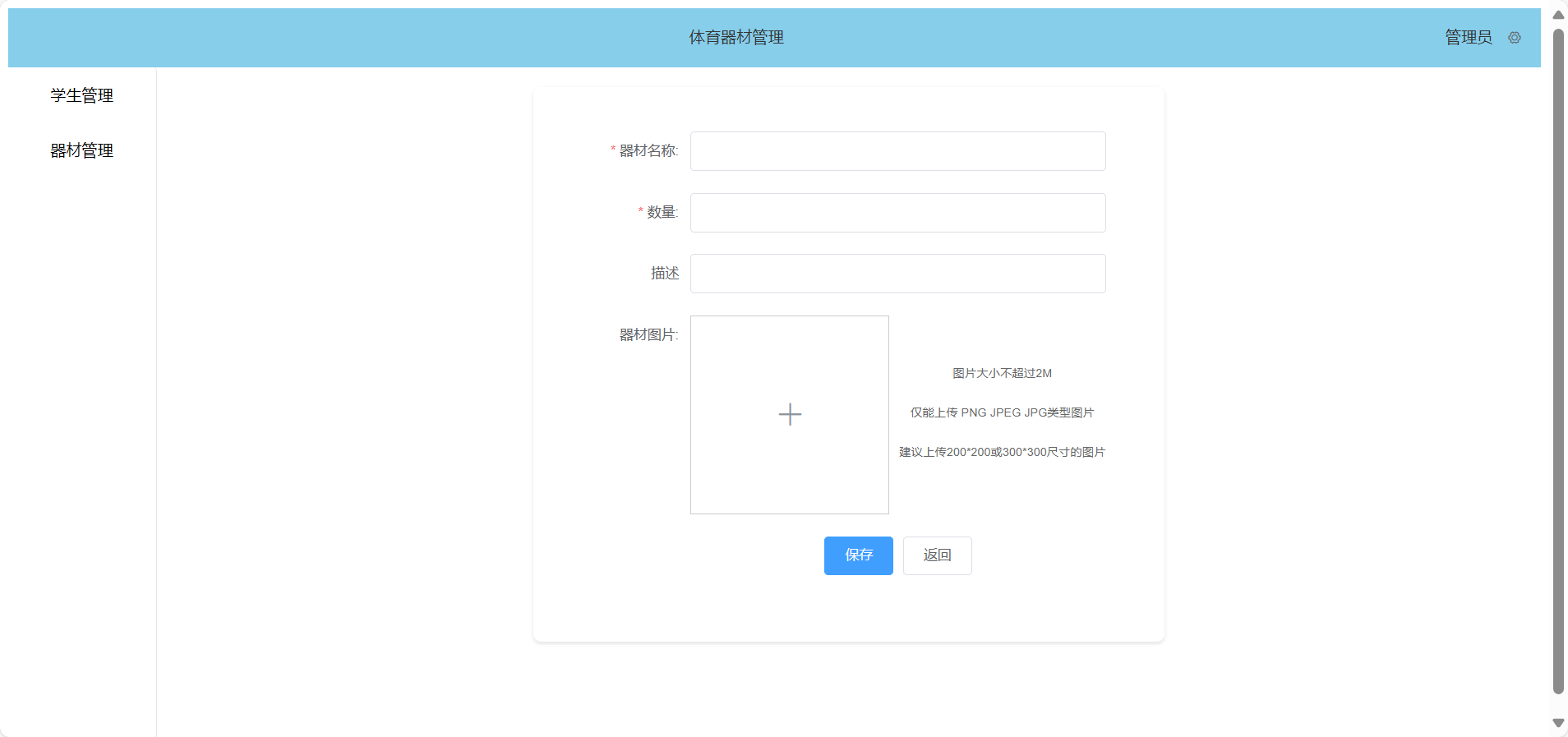
开始尝试从0写一个项目--前端(三)
器材管理板块 添加器材管理导航 src\views\home\Home.vue src\router\index.js src\views\equipment\Equipment.vue <template><div>hello!</div></template> 测试 搜索导航分页查询 src\views\equipment\Equipment.vue <template><div&…...

Visual stdio code 运行C项目环境搭建
参考 [1]VS Code 配置 C/C 编程运行环境(保姆级教程)_visual studio code c配置-CSDN博客 [2]最新VS code配置C/C环境(tasks.json, launch.json,c_cpp_properties.json)及运行多个文件、配置Cmake_vscode launch.json如何配置-CSDN博客 先装visual stdi…...

免杀笔记 -->API的整理Shellcode加密(过DeFender)
最近更新频率明显下降我懒,那么今天就来记录一下我们的一些常用的API的整理以及ShellCode的加密。 1.WinAPI整理 问我为什么要整理? 就是用起来的时候要左翻右翻 :: 烦死了 1.VirtualAlloc VirtualAlloc(NULL,sizeof(buf),MEM_…...

Stable Diffusion 使用详解(3)---- ControlNet
背景 炼丹师在AI绘画的过程中,由于Stable Diffusion的原理是水滴式的扩散作图原理,其实在前面也有提到,他的发挥是‘不稳定’的,因为你没有办法做到精确控制,只能说是大致符合你的预期。你不能总依赖抽卡固定随机数种…...

pythonGame-实现简单的贪食蛇游戏
通过python简单复现贪食蛇游戏。 使用到的库函数: import pygame import time import random 游戏源码: import pygame import time import randompygame.init()white (255, 255, 255) yellow (255, 255, 102) black (0, 0, 0) red (213, 50, 80…...
2024年软件系统与信息处理国际会议(ICSSIP 2024)即将召开!
2024年软件系统与信息处理国际会议(ICSSIP 2024)将于2024年10月25-27日在中国昆明举行。引领技术前沿,共谋创新未来。ICSSIP 2024将汇聚来自世界各地的专家学者,他们将在会上分享最新的研究成果、技术突破及实践经验。会议议题涵盖…...

使用vscode连接开发机进行python debug
什么是debug? 当你刚开始学习Python编程时,可能会遇到代码不按预期运行的情况。这时,你就需要用到“debug”了。简单来说,“debug”就是能再程序中设置中断点并支持一行一行地运行代码,观测程序中变量的变化ÿ…...

(家用)汽车充电桩项目总结分析
1. 项目选题背景 (1)社招:公司想做这个方向,先让学习测试一下,而且不做Web或者APP,以某一个模块或者某一个部分为主 (2)非社招:之前在学校做的一个学习的项目 2. 充电…...

JMeter接口测试:测试中奖概率!
介绍 Apache JMeter 是 Apache 组织基于 Java 开发的压力测试工具,用于对软件做压力测试。JMeter 最初被设计用于 Web 应用测试,但后来扩展到了其他测试领域,可用于测试静态和动态资源,如静态文件、Java 小服务程序、CGI 脚本、J…...

生成式人工智能之路,从马尔可夫链到生成对抗网络
人工智能(Artificial intelligence,AI)技术在过去几年中取得了显著进展,其中生成式AI(Generative AI)因其强大的内容生成能力而备受关注。生成式AI可以创建新的文本、图像、音频、视频、代码以及其他形式的…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
