算法 —— 暴力枚举

目录

循环枚举

P2241 统计方形（数据加强版）

P2089 烤鸡

P1618 三连击（升级版）

子集枚举

P1036 [NOIP2002 普及组] 选数

P1157 组合的输出

排列枚举 

P1706 全排列问题

P1088 [NOIP2004 普及组] 火星人

---

循环枚举

顾名思义，通过for循环或者while循环枚举所有可能方案。 

P2241 统计方形（数据加强版）

很显然这是一道找规律的题目：正方形和长方形的唯一区别在于长宽是否相等，根据此条件可以统计矩形个数，先研究规律：

	for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)

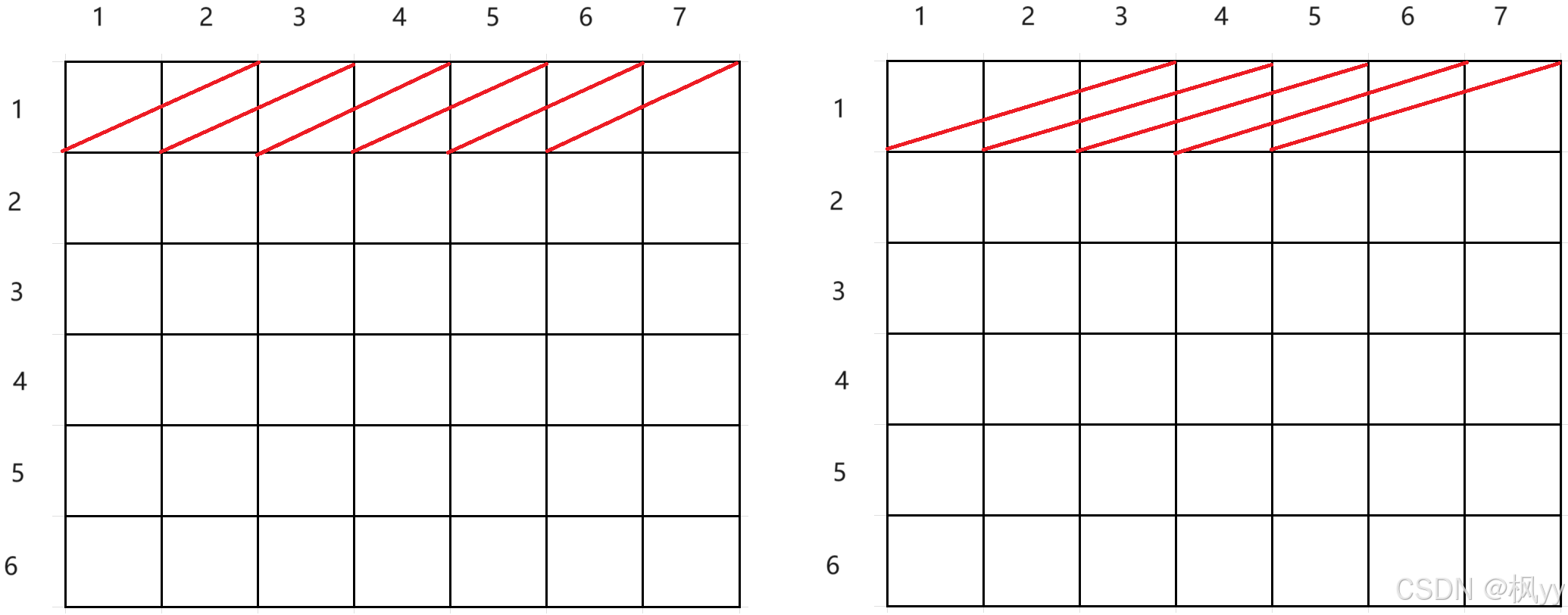
首先是横着的长方形，宽始终为1，长不断发生改变，可以看出长为2的时候，第一行个数为6个，总共有6 x 6个，长为3的时候，总共有6 x 5个……以上述循环条件来看可以得出一个规律：

长发生变化后的矩形总个数为m * ( n - j + 1)个。

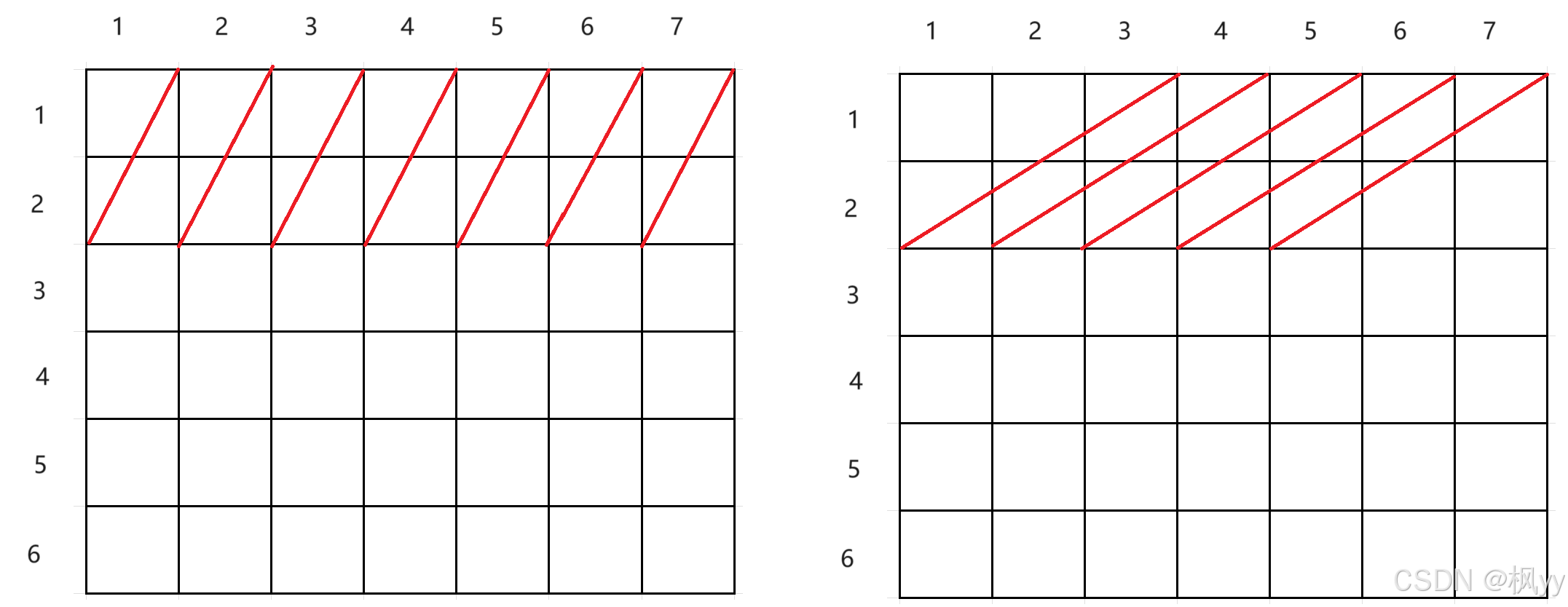
第二看纵向宽发生改变，长重置为1，长为1，宽为2的时候，第一行个数为7个，总共有5 x 7 个，长为2，宽为2的时候 第一行个数为6个，共有5 x 6个……综上所述，可以得出普遍规律：
( m - i + 1) * ( n - j + 1)为每次发生长变化或者宽变化的矩形总个数，又因为长方形与正方形唯一区别是长宽是否相等，因此代码如下：

#include<iostream>
using namespace std;
int main()
{int n, m; cin >> n >> m;long count1 = 0, count2 = 0;for (int i = 1; i <= m; i++)for (int j = 1; j <= n; j++)if (i == j)count1 += (m - i + 1) * (n - j + 1);elsecount2 += (m - i + 1) * (n - j + 1);cout << count1 << ' ' << count2 << endl;return 0;
}

---

P2089 烤鸡

 暴力枚举，用十个循环解决此问题，注意：n如果小于10或者大于30直接输出0即可，原因是十种配料之和最小为10，最大为30。

#include <iostream>
using namespace std;int main()
{int n, count = 0; cin >> n;if (n < 10 || n > 30){cout << 0 << endl;return 0;}else{for (int a = 1; a <= 3; a++)for (int b = 1; b <= 3; b++)for (int c = 1; c <= 3; c++)for (int d = 1; d <= 3; d++)for (int e = 1; e <= 3; e++)for (int f = 1; f <= 3; f++)for (int g = 1; g <= 3; g++)for (int h = 1; h <= 3; h++)for (int i = 1; i <= 3; i++)for (int j = 1; j <= 3; j++)if (a + b + c + d + e + f + g + h + i + j == n)count++;cout << count << endl;for (int a = 1; a <= 3; a++)for (int b = 1; b <= 3; b++)for (int c = 1; c <= 3; c++)for (int d = 1; d <= 3; d++)for (int e = 1; e <= 3; e++)for (int f = 1; f <= 3; f++)for (int g = 1; g <= 3; g++)for (int h = 1; h <= 3; h++)for (int i = 1; i <= 3; i++)for (int j = 1; j <= 3; j++)if (a + b + c + d + e + f + g + h + i + j == n)cout << a << ' ' << b << ' ' << c << ' ' << d << ' ' << e << ' ' << f << ' ' << g << ' ' << h << ' ' << i << ' ' << j << ' ' << endl;}return 0;
}

---

P1618 三连击（升级版）

 本人比较喜欢用stl接口，下面附上代码，注意：输入123，456，789，输出123，456，789

#include<bits/stdc++.h>
using namespace std;int a, b, c, t1, t2, t3; string def;int main()
{cin >> a >> b >> c;for (int i = 1; i <= 1000 / c; i++) //记得从1开始  原因：123，456，789满足{t1 = i * a; t2 = i * b; t3 = i * c;string s1 = to_string(t1), s2 = to_string(t2), s3 = to_string(t3);string tmp; tmp += s1; tmp += s2; tmp += s3;sort(tmp.begin(), tmp.end()); //排序auto it = unique(tmp.begin(), tmp.end()); //去重操作tmp.resize(distance(tmp.begin(), it)); //计算两个迭代器之间的距离if (tmp.size() == 9 && tmp[0] == '1'){cout << s1 << ' ' << s2 << ' ' << s3 << endl;def = tmp;}}if(def.size()==0) //空的说明都不满足cout << "No!!!" << endl;return 0;
}

---

子集枚举

P1036 [NOIP2002 普及组] 选数

这是一道简单的模拟题，枚举出所有可能情况，不会超过规定时间的，以下附上k<=3的代码，如果需要更大的k，继续仿照写即可。

#include <bits/stdc++.h>
using namespace std;int n, k;bool is_prinum(int x)
{for (int i = 2; i <= sqrt(x); i++)if (x % i == 0)return false;return true;
}int main()
{cin >> n >> k;vector<int> arr(n), pri;for (int i = 0; i < n; i++)cin >> arr[i];int count = 0;for (int i = 0; i < n; i++){int tmp = arr[i];if (is_prinum(tmp) && k == 1)count++;if (k == 1)continue;for (int j = i + 1; j < n; j++){int tmp = arr[i] + arr[j];if (is_prinum(tmp) && k == 2)count++;if (k == 2)continue;for (int z = j + 1; z < n; z++){int tmp = arr[i] + arr[j] + arr[z];if (is_prinum(tmp) && k == 3)count++;if (k == 3)continue;}}}cout << count << endl;return 0;
}

---

P1157 组合的输出

与上面一题类似，也是求子集，直接for循环叠加：，下面只举例到3：

#include <bits/stdc++.h>
using namespace std;int n, k;int main()
{cin >> n >> k;vector<string> arr(n), ans;for (int i = 0; i < n; i++)arr[i] = to_string(i + 1);for (int i = 0; i < n; i++){if (k == 1){cout << setw(3) << stoi(arr[i]) << endl;continue;}for (int j = i + 1; j < n; j++){if (k == 2){cout << setw(3) << arr[i] << setw(3) << arr[j] << endl;continue;}for (int z = j + 1; z < n; z++){if (k == 3){cout << setw(3) << arr[i] << setw(3) << arr[j] << setw(3) << arr[z] << endl;continue;}}}}return 0;
}

---

排列枚举 

P1706 全排列问题

本题可以点击此链接看我另一篇文章，其中解释了如何使用stl库的函数解决该问题。

---

P1088 [NOIP2004 普及组] 火星人

本题不过多赘述，与上题一样也是stl的使用，以下为代码：

#include<bits/stdc++.h>
using namespace std;int main()
{int n, m; cin >> n >> m;vector<int> arr(n);for (int i = 0; i < n; i++)cin >> arr[i];for (int j = 1; j <= m; j++)next_permutation(arr.begin(), arr.end());for (auto e : arr)cout << e << ' ';return 0;
}