[C++][STL源码剖析] 详解AVL树的实现
目录
1.概念
2.实现
2.1 初始化
2.2 插入
2.2.1 旋转(重点)
左单旋
右单旋
双旋
2.❗ 双旋后,对平衡因子的处理
2.3 判断测试
完整代码:
拓展:删除
1.概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。
因此,两位俄罗斯的数学家G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右 子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
高度之差=右子树高度 - 左子树高度

AVL == 高度平衡二叉树搜索树
由于AVL树的自平衡特性,它适用于需要频繁插入和删除操作的场景,尤其是对于需要快速搜索和有序遍历的数据集合。
平衡为什么不是高度差相等,而是高度差不超过 1?
为了涵盖更多的情况,例如为节点个数为 4 如下,高度差 1 也相对平衡了

为什么 满二叉树和 AVL 树是同一个 level?
增删查改:高度次->O(logN)
最后一 h 层有 2^(h-1)个节点
满二叉树 2^h-1=N
AVL 树 2^h-X=N //最后一行还存在缺失
X 范围:[1, 2^(h-1)-1]
满二叉树和 AVL 树 在量级上都是约等于 log N 的
2.实现
2.1 初始化
AVL树的节点定义包括以下几个属性:
- 值:每个节点存储的值,可以是任意类型,通常是一个关键字或数据。
- 左子节点指针:指向当前节点的左子节点的指针。左子节点的值应该小于或等于当前节点的值。
- 右子节点指针:指向当前节点的右子节点的指针。右子节点的值应该大于当前节点的值。
- 父节点指针:指向当前节点的父节点的指针。根节点的父节点指针为空。(为了便于后面更好的更新设计的)
- 平衡因子:表示当前节点的左子树高度和右子树高度之差。平衡因子可以为-1、0或1。
下面是一个示例代码来定义一个AVL树的节点结构:
template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0) //balance factor{}
};2.2 插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//if (_root == nullptr){_root = new Node(kv);return true;}//搜索找到位置Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;//小于就右移}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//找到一个为空的位置了生成支点,判断插入
cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//再指回去插入这部分代码倒是没问题,难的是新节点插入后,AVL树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了AVL树,破坏了AVL树就需要旋转调整再次变成AVL树。
如何根据这三种情况来实现插入和对高度的管理?
新增支点:右子树高度++,左子树高度--
插入会对祖先产生影响,平衡因子为 0 了,就再不会对上面的祖先产生影响了,变 0 就平衡了

对以上插入情况,分析可知
是否继续向上更新依旧:子树的高度是否变化
- parent->_bf == 0,说明之前parent->_bf是1或者-1,说明之前parent一边高一边低,而这次的插入是把矮的那边填上了,parent所在子树高度不变,不需要往上继续更新。
- parent->_bf == 1 或者 -1,说明之前parent->_bf为0,两边一样高,现在插入使一边变得更高了,parent所在子树高度变了,继续往上更新。
- parent->_bf == 2 或者 -2,说明之前parent->_bf是1或者-1,现在插入导致严重不平衡,违反规则,就地处理—>旋转。
什么时候结束呢?
_bf==0 或者更新到了根节点的时候
实现平衡因子的更新
// ... 控制平衡// 更新平衡因子while (parent){if (cur == parent->_left){parent->_bf--;}else // if (cur == parent->_right){parent->_bf++;}//判断处理if (parent->_bf == 0){// 更新结束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 继续往上更新cur = parent;parent = parent->_parent;//回指父指针作用的体现,实现上移了}else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要旋转if (parent->_bf == 2 || cur->bf == 1){RotateL(parent);}break;}else{assert(false);}}return true;}接下来我们来看看旋转的实现
2.2.1 旋转(重点)
左单旋
[C++] 详解AVL树左旋的实现~

旋转的时候需要注意的问题:
- 保持他是搜索树
- 变成平衡树且降低这个子树的高度
核心操作:
parent->right=cur->left;
cur->left=parent;如下情况都会用到左旋:


代码:
void RotateL(Node* parent)
{// 保存父节点的右子节点Node* cur = parent->_right;// 保存右子节点的左子节点Node* curleft = cur->_left;// 利用区间性,将子左给父右parent->_right = curleft;if (curleft){// 将右子节点的左子节点作为父节点的右子节点curleft->_parent = parent;}// 将父节点作为右子节点的左子节点cur->_left = parent;// 保存父节点的父节点Node* ppnode = parent->_parent;// 将父节点的父节点指向右子节点parent->_parent = cur;// 判断原父节点是否为根节点if (parent == _root){// 更新根节点为右子节点_root = cur;// 将新根节点的父指针置为空cur->_parent = nullptr;}else{// 判断原父节点是其父节点的左子节点还是右子节点if (ppnode->_left == parent){// 更新父节点的左子节点为右子节点ppnode->_left = cur;}else{// 更新父节点的右子节点为右子节点ppnode->_right = cur;}// 更新右子节点的父指针为父节点的父节点cur->_parent = ppnode;}// 将父节点和右子节点的平衡因子都设置为0,表示树已经平衡parent->_bf = cur->_bf = 0;
}右单旋

代码:
void RotateR(Node* parent)
{// 获取父节点的左子节点Node* cur = parent->_left;// 获取左子节点的右子节点Node* curright = cur->_right;// 将左子节点的右子节点作为父节点的左子节点parent->_left = curright;if (curright){// 更新左子节点的右子节点的父指针curright->_parent = parent;}// 引入父父节点Node* ppnode = parent->_parent;// 将父节点作为左子节点的右子节点cur->_right = parent;// 更新父节点的父指针parent->_parent = cur;// 判断原父节点是否为根节点if (ppnode == nullptr){// 更新根节点为左子节点_root = cur;// 将新根节点的父指针置为空cur->_parent = nullptr;}else{// 判断原父节点是其父节点的左子节点还是右子节点if (ppnode->_left == parent){// 更新父节点的左子节点为左子节点ppnode->_left = cur;}else{// 更新父节点的右子节点为左子节点ppnode->_right = cur;}// 更新左子节点的父指针cur->_parent = ppnode;}// 将父节点和左子节点的平衡因子都设置为0,表示树已经平衡parent->_bf = cur->_bf = 0;
}双旋
左右旋转:插入的两种情况,看的是折线情况
直线:单旋 2 1 同号
折线:双旋 2 -1
旋转判断
根据 parent 和 cur 的平衡因子,实现对使用哪种旋转的判断
else if (parent->_bf == 2 || parent->_bf == -2){// 子树不平衡了,需要旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//异号else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}break;}else{assert(false);}}1.


双旋的结果本质:比 60 小 ,比 30 大的小插入 到 30 下面,找到一个区间中的点
2.❗ 双旋后,对平衡因子的处理
3.h==0 60 本身就是插入的
三种情况,关心 60 的值是-1 0 1
不存在其他奇怪的情况,分别做了 60 的左右

以 RL 为例实现代码:
void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);
//举例思考填写if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}LR 旋转:
平衡因子是根据 curright 初始情况,经过旋转后的图分析分类后得带的

⭕具体而言,先左单旋再右单旋的操作步骤如下:
- 首先获取节点C的左子节点A(subL)和节点A的右子节点D(subLR);
- 然后对节点A进行左单旋(RotateL),此时节点C的左子节点应为节点D,节点D的右子节点应为节点A;
- 最后对节点C进行右单旋(RotateR),此时节点D成为新的子树头节点,节点C成为节点D的右子节点。
最后一部分使用了if语句判断旋转后各个节点的平衡因子,并进行相应的调整,以便使AVL树保持平衡。
- 如果节点D的平衡因子为1,说明节点D的左子树比右子树高,需要进行右旋操作,这一次旋转中节点C和节点A都向右移动了一位,而节点D的平衡因子变为0,节点A和节点C的平衡因子都变为-1;
- 如果节点D的平衡因子为-1,说明节点D的右子树比左子树高,需要进行左旋操作,这一次旋转中节点C和节点A都向左移动了一位,而节点D的平衡因子变为0,节点A和节点C的平衡因子都变为1;
- 如果节点D的平衡因子为0,说明节点D的左右子树高度相等,不需要进行旋转操作,各个节点的平衡因子均设置为0;
- 如果节点D的平衡因子不是1、-1或者0,则说明AVL树已经失去了平衡,这是一个不合法的状态,应该立即报错退出程序。
- 经过这两次旋转后,AVL树重新保持了平衡性和有序性。
void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);
//解耦合,旋转bf 重新定义if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}}2.3 判断测试
test 发现不是根,父亲又是空,是为什么呢?
树的结构出问题了,某次旋转出事了
发现错误就是我们的晋级关键时刻
我们可以根据AVL树的性质来测试
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 即左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
求高度这有个对重载函数的巧妙使用:
当传入的节点
root是nullptr(空指针)时,说明到达了树的叶子节点的下一层,此时返回高度为0,因为空树的高度定义为0。
int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}对于平衡的测试:
IsBalance(Node* root) 是一个递归函数,其工作流程如下:
- 基本情况:如果
root是nullptr,意味着到达了一个空节点,那么认为该子树是平衡的,返回true。- 计算子树高度:计算当前节点的左子树和右子树的高度,分别存储在
leftHight和rightHight变量中。- 检查平衡因子:
root->_bf表示当前节点的平衡因子,即右子树的高度减去左子树的高度。如果计算出的实际高度差与存储的平衡因子不匹配,那么输出错误信息并返回false。这一步是为了验证树的内部数据一致性。- 检查子树平衡性:检查当前节点的左右子树高度差的绝对值是否小于2(即是否平衡)。如果是,则继续递归检查左右子树是否平衡。如果所有的子树都平衡,那么整个树也是平衡的。
bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHight = Height(root->_left);int rightHight = Height(root->_right);if (rightHight - leftHight != root->_bf){cout << "平衡因子异常:" <<root->_kv.first<<"->"<< root->_bf << endl;return false;}return abs(rightHight - leftHight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}private:Node* _root = nullptr;public:int _rotateCount = 0;
};手动制作条件断点,一定要注意父亲回指的设定
// 更新父节点的父指针parent->_parent = cur;对于这个纰漏的处理,来检验和调试这个问题
测试:
int main()
{AVLTree<int, int> tree;// 插入一些节点tree.Insert({10, 10});tree.Insert({20, 20});tree.Insert({30, 30});tree.Insert({40, 40});tree.Insert({50, 50});cout << "树高度: " << tree.Height() << endl;cout << "树是否平衡: " << (tree.IsBalance() ? "是" : "否") << endl;// 插入更多节点来触发旋转tree.Insert({25, 25});tree.Insert({5, 5});tree.Insert({15, 15});cout << "树高度: " << tree.Height() << endl;cout << "树是否平衡: " << (tree.IsBalance() ? "是" : "否") << endl;return 0;
}
发现错误:

拼写错误修正:例如 rotateCount 应为 _rotateCount。parent 不要拼写掉 e。

目前还不知道是为什么,重写了一遍,就跑起来了
完整代码:
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// Update balance factorwhile (parent){if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0)break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1)RotateL(parent);else if (parent->_bf == -2 && cur->_bf == -1)RotateR(parent);else if (parent->_bf == 2 && cur->_bf == -1)RotateRL(parent);else if (parent->_bf == -2 && cur->_bf == 1)RotateLR(parent);break;}else{assert(false);}}return true;}void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else{assert(false);}}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return max(leftHeight, rightHeight) + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}private:Node* _root = nullptr;public:int _rotateCount = 0;
};拓展:删除
插入到 0,不用更改
删除到 0,还要更改
删除会更加的复杂,平衡因子的更新,旋转等等,将上面的思路总结和拓展一下,大家有兴趣可以看看如下的实现代码:
bool Erase(const pair<T, V>& kv)
{if (_root == nullptr)return false;首先,检查树是否为空。如果树为空,直接返回 false,表示删除失败。
Node* parent = nullptr;Node* cur = _root;// 找到要删除的节点while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{break;}}if (cur == nullptr)return false;这部分代码用于在树中查找要删除的节点。通过比较当前节点 cur 的键值 cur->_kv.first 与要删除的键值 kv.first,决定向左子树还是右子树继续搜索。最终,cur 将指向要删除的节点,parent 是 cur 的父节点。如果找不到该键值,返回 false。
// 处理删除节点的三种情况if (cur->_left == nullptr){if (parent == nullptr){_root = cur->_right;if (_root)_root->_parent = nullptr;}else{if (cur == parent->_left){parent->_left = cur->_right;parent->_bf++;}else{parent->_right = cur->_right;parent->_bf--;}if (cur->_right)cur->_right->_parent = parent;}}else if (cur->_right == nullptr){if (parent == nullptr){_root = cur->_left;if (_root)_root->_parent = nullptr;}else{if (cur == parent->_left){parent->_left = cur->_left;parent->_bf++;}else{parent->_right = cur->_left;parent->_bf--;}if (cur->_left)cur->_left->_parent = parent;}}else // 左右子树都不为空{Node* successorParent = cur;Node* successor = cur->_right;while (successor->_left){successorParent = successor;successor = successor->_left;}cur->_kv = successor->_kv;if (successorParent->_left == successor){successorParent->_left = successor->_right;successorParent->_bf++;}else{successorParent->_right = successor->_right;successorParent->_bf--;}if (successor->_right)successor->_right->_parent = successorParent;cur = successor;parent = successorParent;}delete cur;这一部分处理删除节点的三种情况:
- 左子树为空:直接用右子树替代删除节点。如果删除节点是根节点,直接更新根节点
_root。否则,更新父节点的左或右子树指针,并调整平衡因子。 - 右子树为空:直接用左子树替代删除节点。如果删除节点是根节点,直接更新根节点
_root。否则,更新父节点的左或右子树指针,并调整平衡因子。 - 左右子树都不为空:找到右子树中的最小节点(即中序后继节点),用这个节点替代当前节点。然后删除中序后继节点,并调整其父节点的指针和平衡因子。
// 更新平衡因子并处理旋转bool isLRUpdated = true;while (parent){if (!isLRUpdated){if (cur == parent->_left)parent->_bf++;elseparent->_bf--;}isLRUpdated = false;if (parent->_bf == 1 || parent->_bf == -1)return true;else if (parent->_bf == 0){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){Node* higherChild;int sign;if (parent->_bf > 0){sign = 1;higherChild = parent->_right;}else{sign = -1;higherChild = parent->_left;}if (higherChild->_bf == 0){if (sign > 0){RotateL(parent);parent->_bf = 1;higherChild->_bf = -1;}else{RotateR(parent);parent->_bf = -1;higherChild->_bf = 1;}return true;}else if (higherChild->_bf == sign){if (sign == 1)RotateL(parent);elseRotateR(parent);}else{if (sign == 1)RotateRL(parent);elseRotateLR(parent);}cur = parent;parent = cur->_parent;}else{assert(false);}}return true;
}这一部分用于在删除节点后更新平衡因子并处理旋转,以保持树的平衡:
- 平衡因子为 ±1:子树高度没有变化,直接返回。
- 平衡因子为 0:子树高度减少,继续向上更新平衡因子。
- 平衡因子为 ±2:子树严重不平衡,需要旋转。根据较高子树的平衡因子选择合适的旋转方式:
-
- 如果较高子树的平衡因子为 0,进行单旋转。
- 如果较高子树的平衡因子与父节点相同,进行单旋转。
- 如果较高子树的平衡因子与父节点不同,进行双旋转。
通过这些操作,就可以确保树在删除节点后仍然保持平衡啦
相关文章:

[C++][STL源码剖析] 详解AVL树的实现
目录 1.概念 2.实现 2.1 初始化 2.2 插入 2.2.1 旋转(重点) 左单旋 右单旋 双旋 2.❗ 双旋后,对平衡因子的处理 2.3 判断测试 完整代码: 拓展:删除 1.概念 二叉搜索树虽可以缩短查找的效率,但…...

Kubernetes存储 - Node本地存储卷
官方文档 Kubernetes管理的Node本地存储目前有三种,分别是EmptyDir,HostPath,Local,EmptyDir是一种与Pod同生命周期的Node临时存储;HostPath是Node的目录;Local是基于持久卷(PV)管理的Node目录。接下来详细说明这几种类型如何以存…...
Cocos 常见名词)
Cocos Creator2D游戏开发-(2)Cocos 常见名词
场景(Scene): 它一个容器,容纳游戏中的各个元素,如精灵,标签,节点对象。它负责着游戏的运行逻辑,以帧为单位渲染这些内容。就是你理解到的那个场景; 个人理解就是一个画面, 一个游戏不同的关卡,会有不同的…...

【不同设备间的数据库连接】被连接设备如何开权限给申请连接的设备
为了方便叙述,简称申请连接数据库的设备为a,被连接的为b 1.确保在同一局域网下,检查a的ip 如果你设置的动态ip,那么每重启一次这个ip都会变。两种选择,每次都给b同步一下你的最新ip,或者a设置成静态ip。具…...

Whisper离线部署问题处理
Whisper是OpenAI开发一款开源语音识别模型,可以帮我们低成本的拥有语音识别的能力。具体的安装部署方法,我在这里就不详细说了,网上有很多相关文章: 使用OpenAI的Whisper 模型进行语音识别 (baidu.com) 我这里主要想说的是&…...

【Hive SQL】数据探查-数据抽样
文章目录 数据随机抽样1、随机数排序抽样(rand())2、数据块抽样(tablesample())3、分桶抽样 数据随机抽样 在大规模数据量的数据分析及建模任务中,往往针对全量数据进行挖掘分析时会十分耗时和占用集群资源,…...

微信答题小程序产品研发-需求分析与原型设计
欲知应候何时节,六月初迎大暑风。 我前面说过,我决意仿一款答题小程序,所以我做了大量的调研。 题库软件产品开发不仅仅是写代码这一环,它包含从需求调研、分析与构思、设计到开发、测试再到部署上线一系列复杂过程。 需求分析…...

基础模板Mybatis-plus+Springboot+Mysql开发配置文件
1.pom.xml <dependencies><dependency><groupId>org.mybatis.spring.boot</groupId><artifactId>mybatis-spring-boot-starter</artifactId><version>2.2.2</version></dependency>// mybatisplus功能<dependency&g…...

java-poi实现excel自定义注解生成数据并导出
因为项目很多地方需要使用导出数据excel的功能,所以开发了一个简易的统一生成导出方法。 依赖 <dependency> <groupId>org.apache.poi</groupId> <artifactId>poi-ooxml</artifactId> <version>4.0.1</version…...

LeetCode707 设计链表
前言 题目: 707. 设计链表 文档: 代码随想录——设计链表 编程语言: C 解题状态: 代码功底不够,只能写个大概 思路 主要考察对链表结构的熟悉程度,对链表的增删改查,比较考验代码功底以及对链表…...

[Mysql-DDL数据操作语句]
目录 DDL语句操作数据库 库: 查看:show 创建:creat 删除:drop 使用(切换):use 表: 查看:desc show 创建:create 表结构修改 rename as add drop modify change rename as …...
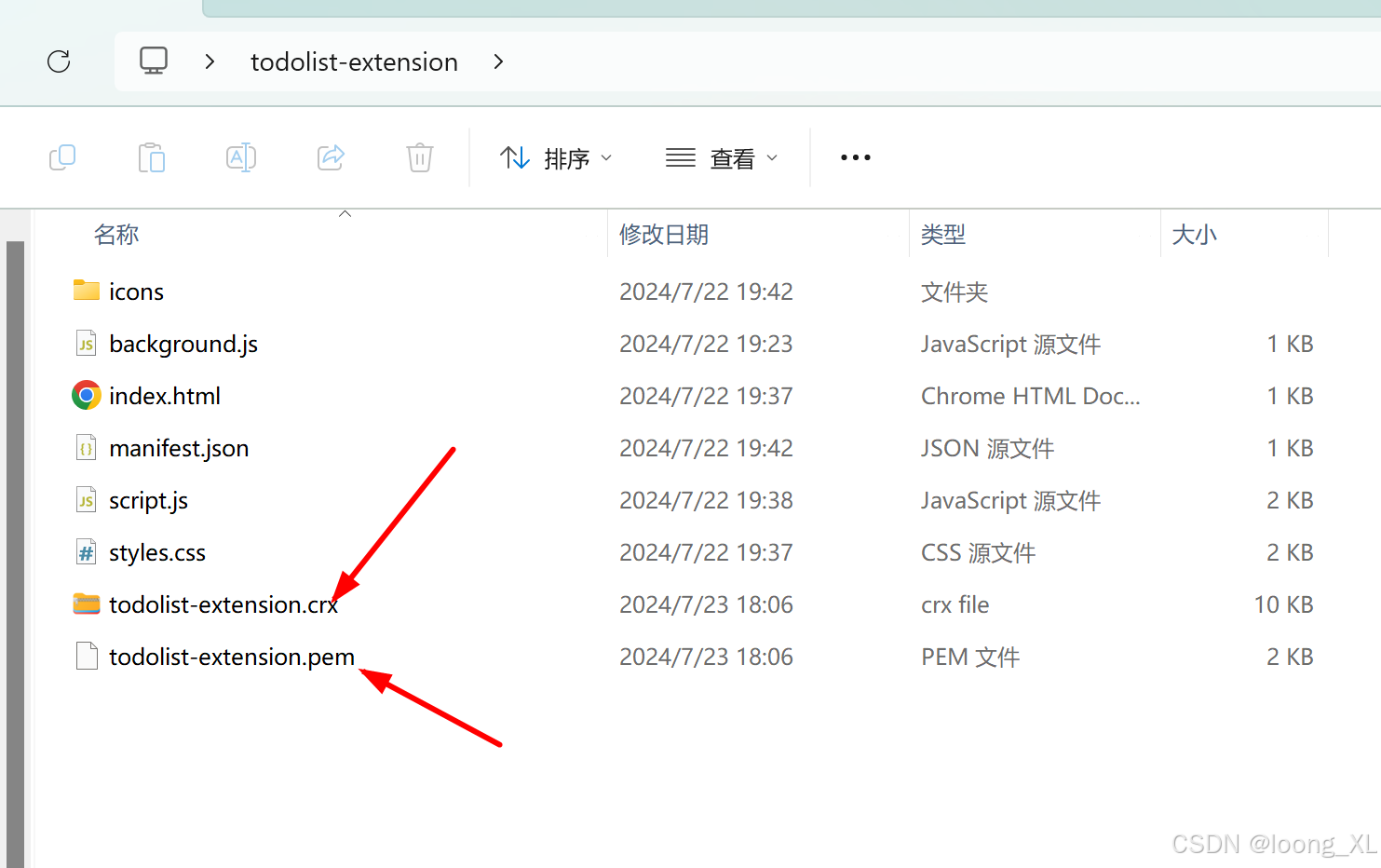
google 浏览器插件开发简单学习案例:TodoList;打包成crx离线包
参考: google插件支持: https://blog.csdn.net/weixin_42357472/article/details/140412993 这里是把前面做的TodoList做成google插件,具体网页可以参考下面链接 TodoList网页: https://blog.csdn.net/weixin_42357472/article/de…...

如何学习Doris:糙快猛的大数据之路(从入门到专家)
引言:大数据世界的新玩家 还记得我第一次听说"Doris"这个名字时的情景吗?那是在一个炎热的夏日午后,我正在办公室里为接下来的大数据项目发愁。作为一个刚刚跨行到大数据领域的新手,我感觉自己就像是被丢进了深海的小鱼—周围全是陌生的概念和技术。 就在这时,我的…...

梯度下降算法,gradient descent algorithm
定义:是一个优化算法,也成最速下降算法,主要的部的士通过迭代找到目标函数的最小值,或者收敛到最小值。 说人话就是求一个函数的极值点,极大值或者极小值 算法过程中有几个超参数: 学习率n,又称…...
)
Spring boot 2.0 升级到 3.3.1 的相关问题 (六)
文章目录 Spring boot 2.0 升级到 3.3.1 的相关问题 (六)spring-data-redis 和 Spring AOP 警告的问题问题描述问题调研结论解决方案方案1-将冲突的Bean 提升为InfrastructureBean方案2 其他相关资料 Spring boot 2.0 升级到 3.3.1 的相关问题 ÿ…...

C++模版基础知识与STL基本介绍
目录 一. 泛型编程 二. 函数模板 1. 概念 2. 函数模版格式 3. 函数模版的原理 4. 模版函数的实例化 (1). 隐式实例化 (2.) 显式实例化 5. 模版参数的匹配原则 三. 类模板 1. 类模板的定义格式 2. 类模板的实例化 四. STL的介绍 1. 什么是STL? 2. STL的版…...

Android 防止重复点击
1.第一种方式: // 两次点击按钮之间的点击间隔不能少于1000毫秒 private static final int MIN_CLICK_DELAY_TIME 700; private static long lastClickTime; /** * 是否是快速点击 * return */ public static boolean isFastClick() { …...

使用阿里云云主机通过nginx搭建文件服务器
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、准备基础环境二、安装配置nginx三、阿里云安全组配置安全组配置 
微信Android一面凉经(2024)
微信Android一面凉经(2024) 笔者作为一名双非二本毕业7年老Android, 最近面试了不少公司, 目前已告一段落, 整理一下各家的面试问题, 打算陆续发布出来, 供有缘人参考。今天给大家带来的是《微信Android一面凉经(2024)》。 面试职位: 微信-客户端开发工程师-基础功能(广州) And…...

VMware、Docker - 让虚拟机走主机代理,解决镜像封禁问题
文章目录 虚拟机全局代理配置找到 VMnet8 的 IPv4 地址代理相关配置虚拟机代理配置 Docker 代理配置修改镜像修改 Docker 代理配置 虚拟机全局代理配置 找到 VMnet8 的 IPv4 地址 a)打开此电脑,输入 “控制面板”,然后回车. b)之…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
