为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义
首先来看一下均值,方差,样本均值与样本方差的定义
总体均值的定义:
μ = 1 n ∑ i = 1 n X i \mu=\frac{1}{n}\sum_{i=1}^{n} X_i μ=n1i=1∑nXi
也就是将总体中所有的样本值加总除以个数,也可以叫做总体的数学期望或简称期望
总体方差的定义:
σ 2 = 1 n ∑ i = 1 n ( X i − μ ) 2 \sigma ^2=\frac {1}{n}\sum_{i=1}^{n} (X_i-\mu)^2 σ2=n1i=1∑n(Xi−μ)2
总体中全部样本各数值与总体均值差的平方和的平均数,用来衡量随机变量或一组数据离散程度的度量。
在实际应用中,我们一般是拿不到总体的均值与总体的方差,只能通过抽样得到的样本均值与样本方差来估计总体的均值与方差。于是我们就得到了样本均值和样本方差:
样本均值的定义
X ˉ = 1 n ∑ i = 1 n X i \bar {X}=\frac{1}{n}\sum_{i=1}^{n} X_i Xˉ=n1i=1∑nXi
样本方差的定义
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2=\frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 S2=n−11i=1∑n(Xi−Xˉ)2
对比总体方差的公式,样本方差的公式的系数为什么变为了 1 n − 1 \frac{1}{n-1} n−11?
通俗理解-自由度
一个比较通俗的的理解就是自由度,可以理解为对应的独立信息量。样本均值和样本方差就是抽样后把所有的独立的信息量(这里的独立的信息量就是数值,包含了均值和方差的信息)平均得到,在计算样本方差时用 X ˉ \bar X Xˉ替代了总体均值 μ \mu μ,自由度减少了一个。
假设只采样了两个样本 X 1 , X 2 X_1,X_2 X1,X2,这其中的信息量是多少呢?方差是计算样本之间的偏离程度,所以一个独立有效的信息量就是这个数值减去均值。在计算方差时分子有两项: ( X 1 − X ˉ ) 2 (X_1-\bar X)^2 (X1−Xˉ)2 和 ( X 2 − X ˉ ) 2 (X_2-\bar X)^2 (X2−Xˉ)2 . 要算第一个样本的偏离程度,毋庸置疑只能老老实实算 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ);但是,第二个样本呢?计算 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 吗?其实还有另外一种方法,因为 X ˉ = X 1 + X 2 2 \bar X=\frac{X_1+X_2}{2} Xˉ=2X1+X2, X 1 X_1 X1 和 X 2 X_2 X2 其实是对于 X ˉ \bar X Xˉ对称的。所以其实 ( X 2 − X ˉ ) = ( 2 X ˉ − X 1 − X ˉ ) = − ( X 1 − X ˉ ) (X_2-\bar X)=(2\bar X-X_1-\bar X)=-(X_1-\bar X) (X2−Xˉ)=(2Xˉ−X1−Xˉ)=−(X1−Xˉ)。也就是我们在用样本均值 X ˉ \bar X Xˉ替代总体均值后,只要 X 1 X_1 X1确定了之后, X 2 X_2 X2是可以根据 X 1 X_1 X1推出来具体数值的,实际能够有效提供样本到 X ˉ \bar X Xˉ的偏移量的信息数只有一条 X 1 X_1 X1。
我们对这种现象可以有一个表述:就是 ( X 2 − X ˉ ) (X_2-\bar X) (X2−Xˉ) 是不自由的,因为从之前的式子可以推出它。当然,对称地,我们也可以说 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)是不自由的。总之,这两个式子当中,只有一个是自由的,所以我们称这两个式子的自由度为 1.所以在两个样本求方差的时候要除1,应为实际应用到方差计算种的只有 ( X 1 − X ˉ ) (X_1-\bar X) (X1−Xˉ)这一个有效信息。
同样,将样本数增加至三个,当有两个样本 X 1 , X 2 X_1,X_2 X1,X2并且知道 X ˉ \bar X Xˉ的情况下,我们就可以推出第三个样本 X 3 X_3 X3的值,对应的自由度为 2.
以此类推,当我们有 n n n个样本的时候,其自由度为 n − 1 n - 1 n−1.也就是说,当我们有 n n n 个样本的时候,我们虽然看起来在分子上做了 n n n 个减法,但实际上我们只算出了 n − 1 n - 1 n−1 个偏差量。因此,做平均的时候,要除以的分母就是 n − 1 n - 1 n−1
但是,为什么 n 个减法做完,自由度只有 n - 1?是谁从中搞鬼,偷走了一个自由度?答案很简单,是 X ˉ \bar X Xˉ 。注意在总体方差中,隐含的分布均值是 μ \mu μ ,这个均值是知道了总体的分布后计算出来的,而在样本方差中 μ \mu μ 是未知的,所以在估计方差之前,我们会需要先找一个 μ \mu μ 的代替,也就是 X ˉ \bar X Xˉ ,而 X ˉ \bar X Xˉ是根据样本算出来的. 也就是说,在用 X ˉ \bar X Xˉ 代替 μ \mu μ 的过程中,我们损失了一个自由度。
那么,如果问题的背景变了,我们知道隐含的分布均值 μ \mu μ ,只是不知道 σ 2 \sigma^2 σ2 ,那我们该如何估计 σ 2 \sigma^2 σ2?这种情况下求方差就变成了符合直觉的 ( X 1 − μ ) 2 + ( X 2 − μ ) 2 + ⋯ + ( X n − μ ) 2 n \frac{(X_1-\mu)^2+(X_2-\mu)^2+\dots+(X_n-\mu)^2}{n} n(X1−μ)2+(X2−μ)2+⋯+(Xn−μ)2。
严密推导过程
估计量的评选标准
当我们用抽样的方法去估计总体时,总是希望每次抽样的结果尽可能的靠近实际的总体评估量,同时抽取的样本越多时越接近实际的总体评估量。对于评估量的好坏有如下三个评价指标
无偏性
设 θ \theta θ是总体的未知参数, X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn是总体的一个样本, θ ^ \widehat \theta θ 是参数的一个估计量,若
E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ
则称 θ ^ \widehat \theta θ 是 θ \theta θ的一个无偏估计量
无偏性简单来说就是取样后得到的估计量 θ ^ \widehat \theta θ 的期望就等于总体的估计量。
考虑如下一个打靶的例子。如果有一个射击高手打靶,那么结果总会在靶心附近(总体期望 θ \theta θ),那么我们一般会通过打靶结果(也就是样本 θ ^ \widehat \theta θ )认为这是一个熟练的射击手,对于多次的打靶结果我们对其打靶结果的期望是靶心( E ( θ ^ ) = θ E(\widehat \theta)=\theta E(θ )=θ),也就是无偏的。
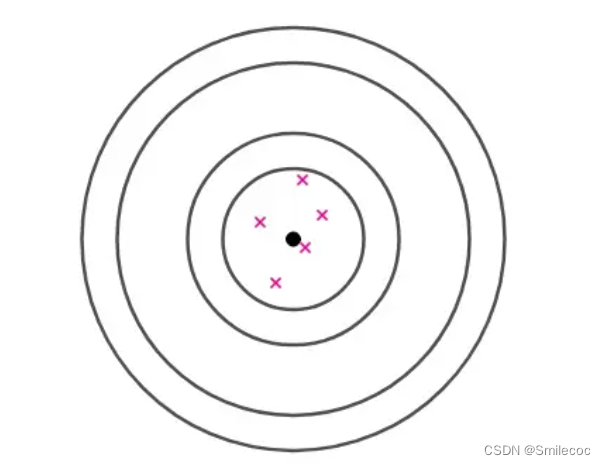
但如果出现了如下这种结果,通过这些样本我们就会猜测集中在一点附近可能是一个射击高手,这个偏差可能是由于瞄准镜歪了这种导致的呢
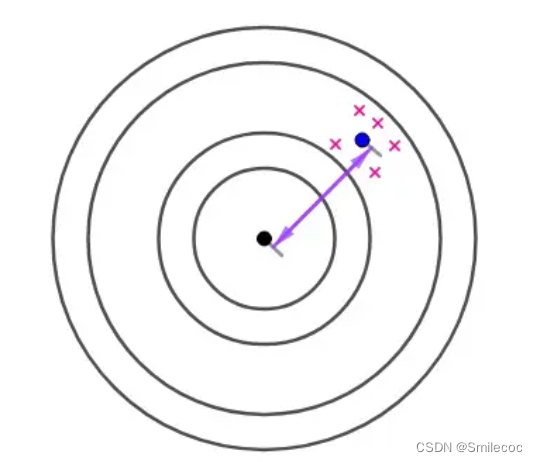
对于这种稳定影响结果的因素导致的偏差称为系统偏差,也就是 E ( θ ^ ) − θ E(\widehat \theta)-\theta E(θ )−θ。无偏估计的实际意义就是无系统偏差。很明显无偏估计更接近实际的总体统计量
有效性
若 θ ^ 1 {\widehat \theta}_1 θ 1和 θ ^ 2 {\widehat \theta}_2 θ 2都是样本 X 1 , X 2 , . . . . . X n X_1,X_2,.....X_n X1,X2,.....Xn的无偏估计量,若对于任意取值范围里有 D ( θ ^ 1 ) ≤ D ( θ ^ 2 ) D({\widehat \theta}_1) \le D({\widehat \theta}_2) D(θ 1)≤D(θ 2),
则 θ ^ 1 {\widehat \theta}_1 θ 1比 θ ^ 2 {\widehat \theta}_2 θ 2更加有效。
有效性就是同样无偏的估计量,更集中,方差更小的估计量更好
接着考虑如下打靶结果,虽然期望都是靶心,但是很明显后面的结果更加集中,相应的评估效果也会更好
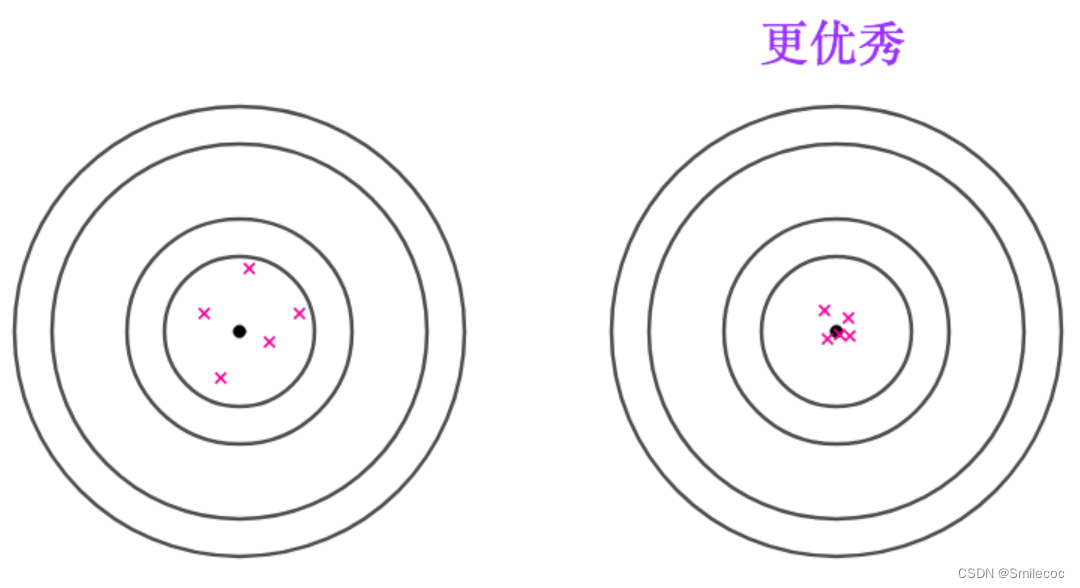
相合性
之前的无偏性和一致性都是在样本容量固定为n的情况下讨论的,而如果样本容量越来越多时,一个估计量能稳定于待估的参数真值
相合性大样本条件下,估计值等于实际值.对于任意 θ > 0 \theta >0 θ>0,有
lim n → ∞ P ( ∣ θ ^ − θ ∣ < ε ) = 1. \lim\limits_{n\to\infty}P\left(|\hat\theta-\theta| < \varepsilon\right)=1. n→∞limP(∣θ^−θ∣<ε)=1.
推导
首先来看一下在分母为n的情况下样本方差是不是总体方差的无偏估计量:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) − ( X ˉ − μ ) ) 2 ] = E [ 1 n ∑ i = 1 n ( ( X i − μ ) 2 − 2 ( X i − μ ) ( X ˉ − μ ) + ( X ˉ − μ ) 2 ) ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + 1 n ( X ˉ − μ ) 2 ∑ i = 1 n 1 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)-(\bar X - \mu) \Bigg)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} \Bigg( (X_i - \mu)^2-2(X_i - \mu)(\bar X - \mu)+(\bar X - \mu)^2 \Bigg) \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ \frac{1}{n} (\bar X - \mu)^2 \sum_{i=1}^{n} 1 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−Xˉ)2]=E n1i=1∑n((Xi−μ)−(Xˉ−μ))2 =E[n1i=1∑n((Xi−μ)2−2(Xi−μ)(Xˉ−μ)+(Xˉ−μ)2)]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+n1(Xˉ−μ)2i=1∑n1]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]
其中
X ˉ − μ = 1 n ∑ i = 1 n X i − 1 n ∑ i = 1 n μ = 1 n ∑ i = 1 n ( X i − μ ) \bar X - \mu=\frac{1}{n}\sum_{i=1}^{n} X_i-\frac{1}{n}\sum_{i=1}^{n} \mu=\frac{1}{n}\sum_{i=1}^{n} (X_i-\mu) Xˉ−μ=n1i=1∑nXi−n1i=1∑nμ=n1i=1∑n(Xi−μ)
接着计算有:
E ( S 2 ) = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ∑ i = 1 n ( X i − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − 2 n ( X ˉ − μ ) ⋅ n ⋅ ( X ˉ − μ ) + ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 − ( X ˉ − μ ) 2 ] = E [ 1 n ∑ i = 1 n ( X i − μ ) 2 ] − E [ ( X ˉ − μ ) 2 ] = σ 2 − E [ ( X ˉ − μ ) 2 ] \begin{aligned} E(S^2) &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \sum_{i=1}^{n}(X_i - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- \frac{2}{n} (\bar X - \mu) \cdot n \cdot (\bar X - \mu)+ (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2- (\bar X - \mu)^2 \right ] \\ &= E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \mu)^2 \right ]- E \bigg [(\bar X - \mu)^2 \bigg ] \\ &= \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] \end{aligned} E(S2)=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)i=1∑n(Xi−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−n2(Xˉ−μ)⋅n⋅(Xˉ−μ)+(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2−(Xˉ−μ)2]=E[n1i=1∑n(Xi−μ)2]−E[(Xˉ−μ)2]=σ2−E[(Xˉ−μ)2]
可以看到同样在除以 n n n的情况下只有当 X ˉ = μ \bar X = \mu Xˉ=μ时才有 E ( S 2 ) = σ 2 E(S^2)= \sigma^2 E(S2)=σ2,在其他情况下 E ( S 2 ) E(S^2) E(S2)都是小于 σ 2 \sigma^2 σ2的。这一个结果也很好理解,只要样本均值 X ˉ \bar X Xˉ越偏离总体均值 μ \mu μ,样本也就越偏离总体均值。
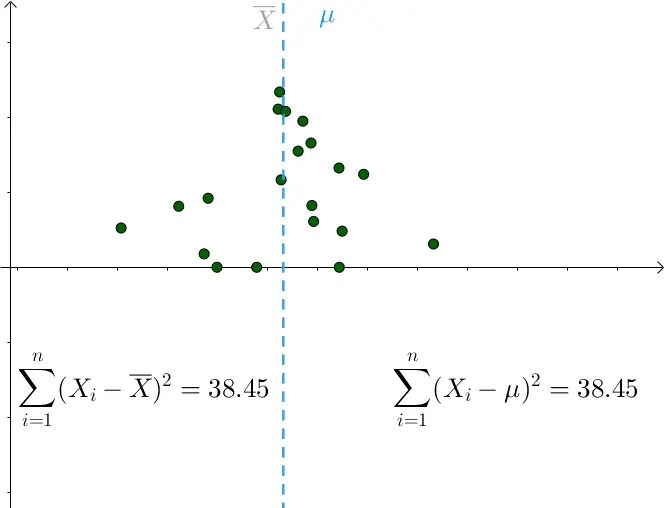
接下来就是要计算出差异 E [ ( X ˉ − μ ) 2 ] E \bigg [(\bar X - \mu)^2 \bigg ] E[(Xˉ−μ)2]是多少
由
E ( X ˉ ) = E ( 1 n ∑ i = 1 n X i ) = 1 n ∑ i = 1 n E ( X i ) = 1 n ∑ i = 1 n μ = μ E(\bar{X}) = E\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg) = \frac{1}{n}\sum_{i=1}^nE(X_i) = \frac{1}{n}\sum_{i=1}^n \mu = \mu E(Xˉ)=E(n1i=1∑nXi)=n1i=1∑nE(Xi)=n1i=1∑nμ=μ
D ( a X i ) = a 2 D ( X i ) D(aX_i) = a^2 D(X_i) D(aXi)=a2D(Xi)
代入有:
E [ ( X ˉ − μ ) 2 ] = E [ ( X ˉ − E ( X ˉ ) ) 2 ] = D ( X ˉ ) = D ( 1 n ∑ i = 1 n X i ) = 1 n 2 ∑ i = 1 n D ( X i ) = 1 n 2 ⋅ n σ 2 = σ 2 n \begin{aligned} E \bigg [(\bar X - \mu)^2 \bigg ] &= E \bigg [(\bar X - E(\bar{X}))^2 \bigg ] \\ &=D(\bar{X})\\ &=D\bigg(\frac{1}{n} \sum_{i=1}^{n} X_i\bigg)\\ &=\frac{1}{n^2} \sum_{i=1}^{n} D(X_i) \\ &=\frac{1}{n^2} \cdot n \sigma^2 \\ &=\frac{\sigma^2}{n} \end{aligned} E[(Xˉ−μ)2]=E[(Xˉ−E(Xˉ))2]=D(Xˉ)=D(n1i=1∑nXi)=n21i=1∑nD(Xi)=n21⋅nσ2=nσ2
所以
E ( S 2 ) = σ 2 − E [ ( X ˉ − μ ) 2 ] = n − 1 n σ 2 E(S^2) = \sigma^2-E \bigg [(\bar X - \mu)^2 \bigg ] =\frac{n-1}{n}\sigma^2 E(S2)=σ2−E[(Xˉ−μ)2]=nn−1σ2
进行一下调整,即有
n n − 1 E ( S 2 ) = n n − 1 E [ 1 n ∑ i = 1 n ( X i − X ˉ ) 2 ] = E [ 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 ] = σ 2 \frac{n}{n-1}E(S^2)=\frac{n}{n-1} E \left [ \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=E \left [ \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \bar X)^2 \right ]=\sigma^2 n−1nE(S2)=n−1nE[n1i=1∑n(Xi−Xˉ)2]=E[n−11i=1∑n(Xi−Xˉ)2]=σ2
这样得到的就是无偏的估计
https://www.zhihu.com/question/20099757
https://www.zhihu.com/question/22983179
相关文章:

为什么样本方差(sample variance)的分母是 n-1?
样本均值与样本方差的定义 首先来看一下均值,方差,样本均值与样本方差的定义 总体均值的定义: μ 1 n ∑ i 1 n X i \mu\frac{1}{n}\sum_{i1}^{n} X_i μn1i1∑nXi 也就是将总体中所有的样本值加总除以个数,也可以叫做总…...

编解码器架构
一、定义 0、机器翻译是序列转换模型的一个核心问题, 其输入和输出都是长度可变的序列。 为了处理这种类型的输入和输出, 我们设计一个包含两个主要组件的架构: 第一个组件是一个编码器(encoder): 它接受一…...

追问试面试系列:JVM运行时数据区
hi 欢迎来到追问试面试系列之JVM运行时数据区,在面试中出现频率非常高,并且其中还存在一些误导性的面试,一定要注意。 什么误导性呢?面试中,有的面试官本来是想问JVM运行时数据区,不过提问时难免有些让你觉得很不爽。比如:你说说java内存模型,还比如说说JVM内存模型,…...

React Native在移动端落地实践
在移动互联网产品迅猛发展的今天,技术的不断创新使得企业越来越注重降低成本、提升效率。为了在有限的开发资源下迅速推出高质量、用户体验好的产品,以实现公司发展,业界催生了许多移动端跨平台解决方案。这些方案不仅简化了开发流程…...

《操作系统》(学习笔记)(王道)
一、计算机系统概述 1.1 操作系统的基本概念 1.1.1 操作系统的概念 1.1.2 操作系统的特征 1.1.3 操作系统的目标和功能 1.2 操作系统的发展与分类 1.2.1 手工操作阶段(此阶段无操作系统) 1.2.2 批处理阶段(操作系统开始出现࿰…...

LabVIEW学习-LabVIEW处理带分隔符的字符串从而获取数据
带分隔符的字符串很好处理,只需要使用"分隔符字符串至一维字符串数组"函数或者"一维字符串数组至分隔符字符串"函数就可以很轻松地处理带分隔符地字符串。 这两个函数所在的位置为: 函数选板->字符串->附加字符串函数->分…...

freesql简单使用操作mysql数据库
参考:freesql中文官网指南 | FreeSql 官方文档 这两天准备做一个测试程序,往一个系统的数据表插入一批模拟设备数据,然后还要模拟设备终端发送数据包,看看系统的承压能力。 因为系统使用的第三方框架中用到了freesql,…...

使用Java和Spring Retry实现重试机制
使用Java和Spring Retry实现重试机制 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将探讨如何在Java中使用Spring Retry来实现重试机制。重试机制在处理临时性故障和提高系统稳…...
:自定义配置与插件管理)
Linux Vim教程(十):自定义配置与插件管理
目录 1. 概述 2. Vim 配置文件 2.1 .vimrc 文件 2.2 .gvimrc 文件 3. 自定义配置 3.1 自定义快捷键 3.2 自动命令 3.3 函数定义 4. 插件管理 4.1 插件管理工具 4.1.1 安装 vim-plug 4.1.2 配置 vim-plug 4.1.3 安装插件 4.2 常用插件 4.2.1 NERDTree 4.2.2 Fzf…...

代理协议解析:如何根据需求选择HTTP、HTTPS或SOCKS5?
代理IP协议是一种网络代理技术,可以实现隐藏客户端IP地址、加速网站访问、过滤网络内容、访问内网资源等功能。常用的IP代理协议主要有Socks5代理、HTTP代理、HTTPS代理这三种。代理IP协议主要用于分组交换计算机通信网络的互联系统中使用,只负责数据的路…...
Verilog语言和C语言的本质区别是什么?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「C语言的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 用老石的一句话其实很好说…...

Delphi5实现鱼C屏幕保护程序
效果图 鱼C屏幕保护程序 添加背景图片 在additional添加image组件,修改picture属性上传图片。 这个图片可以截屏桌面,方便后面满屏不留白操作。实现无边框 即上面的“- □ ”不显示 将Form1的borderstyle属性改为bsnone实现最大化,满屏 将…...

【计算机毕业设计】844学籍管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

Java之开发 系统设计 分布式 高性能 高可用
1、restful api 基于rest构建的api 规范: post delete put get 增删改查路径 接口命名 过滤信息状态码 2、软件开发流程 3、命名规范 类名:大驼峰方法名:小驼峰成员变量、局部变量:小驼峰测试方法名:蛇形命名 下划…...

java连接redis和基础操作命令
引入依赖 <!--引入java连接redis的驱动--><dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId><version>4.3.1</version></dependency> 单机模式连接redis main(){ //连接redis的信息 默认连接…...

土耳其云手机提升TikTok电商效率
在数字化飞速发展的今天,TikTok不仅是一个社交平台,更是一个巨大的电商市场。随着TikTok电商功能在全球范围内的扩展,土耳其的商家和内容创作者正面临着前所未有的机遇。本文将详细介绍土耳其云手机怎样帮助商家抓住机遇,实现业务…...

《Utilizing Ensemble Learning for Detecting Multi-Modal Fake News》
系列论文研读目录 文章目录 系列论文研读目录论文题目含义ABSTRACTINDEX TERMSI. INTRODUCTIONII. RELATED WORKA. FAKE NEWS CLASSIFICATION APPROACHES FOR SINGLE-MODALITY 单模态虚假新闻分类方法1) SINGLE-MODALITY BASED CLASSIFICATION APPROACHES USING TEXTUAL FEATUR…...

Oracle集群RAC磁盘管理命令asmcmd的使用
文章目录 ASM磁盘共享简介ASM磁盘共享的优势ASM磁盘组成ASM磁盘共享的应用场景Asmcmd简介Asmcmd的功能Asmcmd的命令Asmcmd的使用注意事项Asmcmd运行模式交互模式运行非交互模式运行ASMCMD命令分类实例管理命令:文件管理命令:磁盘组管理命令:模板管理命令:文件访问管理命令:…...

vscode插件开发笔记——大模型应用之AI编程助手
系列文章目录 文章目录 系列文章目录前言一、代码补全 前言 最近在开发vscode插件相关的项目,网上很少有关于大模型作为AI 编程助手这方面的教程。因此,借此机会把最近写的几个demo分享记录一下。 一、代码补全 思路: 读取vscode插件上鼠…...

@JSONField(format = “yyyyMMddHH“)的作用和使用
JySellerItqrdDataDO对象中的字段为: private Date crdat; 2.数据库中的相应字段为: crdat datetime DEFAULT NULL COMMENT 创建时间,2. 打印出的结果为: “crdat”:“2024072718” 年月日时分秒 3. 可以调整format的格式 4. 这样就把Date类…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...
