图中的最短环

2608. 图中的最短环

现有一个含 n 个顶点的 双向 图，每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接，并且不存在与自身相连的顶点。

返回图中 最短 环的长度。如果不存在环，则返回 -1 。

环 是指以同一节点开始和结束，并且路径中的每条边仅使用一次。

示例 1：

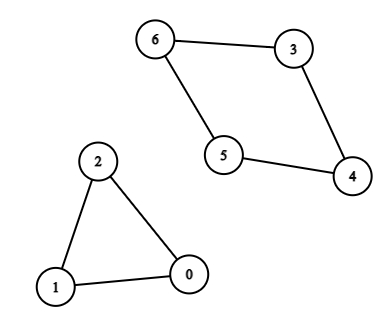
**输入：**n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
**输出：**3
**解释：**长度最小的循环是：0 -> 1 -> 2 -> 0

示例 2：

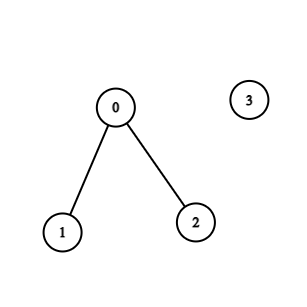
**输入：**n = 4, edges = [[0,1],[0,2]]
**输出：**-1
**解释：**图中不存在循环

提示：

• 2 <= n <= 1000
• 1 <= edges.length <= 1000
• edges[i].length == 2
• 0 <= ui, vi < n
• ui != vi
• 不存在重复的边

还是删除边比较容易写

class Solution {
public:int findShortestCycle(int n, vector<vector<int>>& edges) {for (int i = 0; i < 1000; i++) fa[i] = i;vector<pair<int, int>> sto; // 存储环的起始和结束节点for (auto u : edges) {int x = find(u[0]), y = find(u[1]);if (x != y) {fa[x] = y;}else {sto.push_back({ u[0],u[1] });}e[u[0]].push_back(u[1]);e[u[1]].push_back(u[0]);}if (sto.size() == 0) return -1;int ans = 0xffffff;for (auto [u,v] : sto) {queue<pair<int, int>> q;vector<bool> vis(n + 1, 0);q.push({ u,1 });while (q.size()) {auto [node, step] = q.front(); q.pop();if (node == v) {ans = min(ans, step); break;}if (vis[node]) continue;vis[node] = 1;for (auto to : e[node]) {if (node == u && to == v) continue; // 跳开一条断边q.push({ to,step + 1 });}}}return ans;}int find(int x) {if (x == fa[x]) return x;return fa[x] = find(fa[x]);}int fa[1001];vector<int> e[1001];};

我们再看一个题目，如果权重

#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
using namespace std;const int N = 105;
int e[N][N];
int n,m;
const int M = (int)5e3+5;
int edge[M],ne[M],h[N],idx = 0;
int w[M];
int fa[N];void add(int a,int b,int wei){edge[++idx] = b, ne[idx] = h[a], h[a] = idx;w[idx] = wei;
}int find(int x){if(x==fa[x]) return x;return fa[x] = find(fa[x]);
}int main(){cin >> n >> m;// 开始处理fafor(int i=0;i<=n;i++) fa[i] = i; vector<pair<int,int>> sto;for(int i=1;i<=m;i++){int u,v,d;cin >> u >> v >> d;if(e[u][v]==0){e[u][v] = d;e[v][u] = d;}else{if(e[u][v]>d){e[u][v] = d;e[v][u] = d;}}}	for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){if(e[i][j]){int x = find(i), y = find(j);if(x!=y) fa[x] = y;else {sto.push_back({i,j});}add(i,j,e[i][j]);add(j,i,e[i][j]);}}}
//	if(sto.size()==0) {
//		cout << "No solution."; return 0;
//	}int ans = 0x7fffffff;for(auto x:sto){vector<bool> vis(n+1);int u = x.first, v = x.second;priority_queue<pair<int,int>> q;q.push({0,u});while(q.size()){int d = -q.top().first, node = q.top().second; q.pop();if(vis[node]) continue;vis[node] = 1;if(node==v){ans = min(ans,d+e[v][u]); break;}for(int i=h[node];i;i=ne[i]){int to = edge[i], ww = w[i];if(node==u&&to==v) continue;q.push({-(d+ww),to});}}}if(ans!=0x7fffffff)cout << ans;else cout << "No solution."; return 0;
}