计算机中的浮点数运算
计算机中的浮点数
计算机中以固定长度存储浮点数的方式,造成了浮点数运算过程容易产生上溢和下溢。以float32为例, 其标记位占1bit,指数位占8bit,小数部分占23bit

经典下溢场景
不满足精度导致截断误差
#include <iostream>
#include <iomanip>
using namespace std;
int main() {float a = 1.f;float eps = 1e-8f;float c = a + eps;cout << setprecision(16) << a << "+" << eps << "=" << c << endl;return 0;
}
微小的误差很容易被放大
这里以二元一次方程的求根为例
ax2+bx+c=0ax^{2}+bx+c=0ax2+bx+c=0
根据基础数学知识,你会给出这样一个解决方案
x1,2=−b±b2−4ac2ax_{1,2} = \frac{-b\pm \sqrt {b^2-4ac}}{2a}x1,2=2a−b±b2−4ac
由此设计程序
#include<iostream>
#include<cmath>
using namespace std;int main() {float a, b, c;float temp, root, r1, r2;cout << "该程序用于求一元二次方程ax^2+bx+c=0的解" << endl;cout << "请依次输入a b c的值(a不要为0)" << endl;cin >> a >> b >> c;temp = b * b - 4 * a * c;root = sqrt(temp);if (temp < 0) {cout << "改方程无解\n";return -1;}r1 = (-b + root) / 2.0 / a;r2 = (-b - root) / 2.0 / a;cout << "一元二次方程的解为:" << r1 << " , " << r2 << endl;return 0;
}
使用这段程序输入 0.01,1000,10.01,1000,10.01,1000,1
输出−0.00305176,−100000-0.00305176 , -100000−0.00305176,−100000
而保留小数点后六位有效数字应该是−0.001000,−99999.990000-0.001000,-99999.990000−0.001000,−99999.990000
此时,第一项的相对误差为百分之两百,而第二项的相对误差为千万分之一。
显然,两个相近的数相减会使得运算后的有效位数变少,也就是在a,ca,ca,c的值很小时, $ -b + \sqrt {b^2-4ac}$ 这一操作过后,使得实际结果的有效位变低了(或者说引入了较大的误差),并且这个误差会在后续的运算中被放大。
这时可以通过数学手段减少误差
既然 x1,2=−b±b2−4ac2ax_{1,2} = \frac{-b\pm \sqrt {b^2-4ac}}{2a}x1,2=2a−b±b2−4ac
分子分母同时乘以 −b−b2−4ac,−b+b2−4ac-b - \sqrt {b^2-4ac},-b + \sqrt {b^2-4ac}−b−b2−4ac,−b+b2−4ac 可得
$x_{1} = \frac{2c}{-b - \sqrt {b^2-4ac}} , x_{2} =\frac{2c}{-b + \sqrt {b^2-4ac}} $
根据b 的正负性,两个求根公式各取一半得到新的算法
新算法的结果为−0.001,−10000-0.001 , -10000−0.001,−10000
#include<iostream>
#include<cmath>
using namespace std;int main() {float a, b, c;float temp, root, r1, r2;cout << "该程序用于求一元二次方程ax^2+bx+c=0的解" << endl;cout << "请依次输入a b c的值(a不要为0)" << endl;cin >> a >> b >> c;temp = b * b - 4 * a * c;root = sqrt(temp);if (temp < 0) {cout << "改方程无解\n";return -1;}if (b > 0) {r1 = 2 * c / (-b - root);r2 = (-b - root) / 2 / a;}else if (b < 0) {r1 = (-b + root) / 2 / a;r2 = 2 * c / (-b + root);}else {temp = c / a;r1 = sqrt(-temp);r2 = -sqrt(-temp);}cout << "一元二次方程的解为:" << r1 << " , " << r2 << endl;return 0;
}
相关文章:

计算机中的浮点数运算
计算机中的浮点数 计算机中以固定长度存储浮点数的方式,造成了浮点数运算过程容易产生上溢和下溢。以float32为例, 其标记位占1bit,指数位占8bit,小数部分占23bit 经典下溢场景 不满足精度导致截断误差 #include <iostream> #include <iomanip> usin…...

看了字节跳动月薪20K+测试岗面试题,让我这个工作3年的测试工程师,冷汗直流....
朋友入职已经两周了,整体工作环境还是非常满意的!所以这次特意抽空给我写出了这份面试题,而我把它分享给伙伴们,面试&入职的经验! 大概是在2月中的时候他告诉我投递了字节跳动并且简历已通过,2月23经过…...
这两天最好的ChatGPT应用;使用Notion AI提升效率的经验(13);AI编程与程序员的生存 | ShowMeAI日报
👀日报合辑 | 🎡生产力工具与行业应用大全 | 🧡 点赞关注评论拜托啦! 🤖 硅谷银行风波中,OpenAI 创始人大方帮助硅谷初创公司:钱先拿着用,有了再还 OpenAI 创始人 Sam Altman 的弟弟…...

Linux 内核likely与unlikey
内核源码的时候经常可以看到likely()和unlikely()函数,这两个函数的作用是什么?-- 先得学一学GCC提供的内建函数!! likely和unlikely内核中的定义 # define likely(x) __builtin_expect(!!(x), 1) # define unlikely(x) __built…...

成功解决主从同步异常之Slave_IO_Running显示为No的问题
前言 MySQL主从同步在做的过程中很容易出问题, 尤其是双主配置,参数多,需要在两台服务器中反复操作,容易搞错导致失败,这里汇总的是主从同步异常之Slave_IO_Running显示为No的解决方案。 文章目录 前言一. 问题重现二. 排查过程2.1 查看UUID是否相同,并修改2.2 修改完UU…...

面试阿里测开岗失败后,被面试官在朋友圈吐槽了......
前一阵子有个徒弟向我诉苦,说自己在参加某大厂测试面试的时候被面试官怼得哑口无言,场面让他一度十分尴尬印象最深的就是下面几个问题:根据你以前的工作经验和学习到的测试技术,说说你对质量保证的理解?非关系型数据库…...

蓝桥杯嵌入式--字符串比较在串口通信中的应用
前言今天做了个模拟题,大致意思是接收上位机发的字符串,然后执行相应操作。思路很明确,就是把接收到的内容进行比较,但是从前我只学过比较数字的方式,即直接用“”进行比较,但是字符串不能使用这个方法&…...
考研408每周一题(2019 41)
2019年(单链表) 41.(13分)设线性表L(a1,a2,a3,...,a(n-2),a(n-1),an)采用带头结点的单链表保存,链表中的结点定义如下: typedef struct node {int data;struct node *next; } NODE; 请设计一个空间复杂度为O(1)且时间上尽可能高效的算法&…...
)
Angular学习笔记(一)
以下内容基于Angular 文档中文版的学习 目录 使用Angular CLI 工具创建项目 HTML标签中{{}}插入值,[]绑定属性,()绑定事件,[(ngModel)]双向绑定 绑定属性 类和样式绑定 事件绑定 双向绑定 循环 IF 定义输入属性 定义输出事件 特殊符号 模板引用变量 页面跳转(路由…...
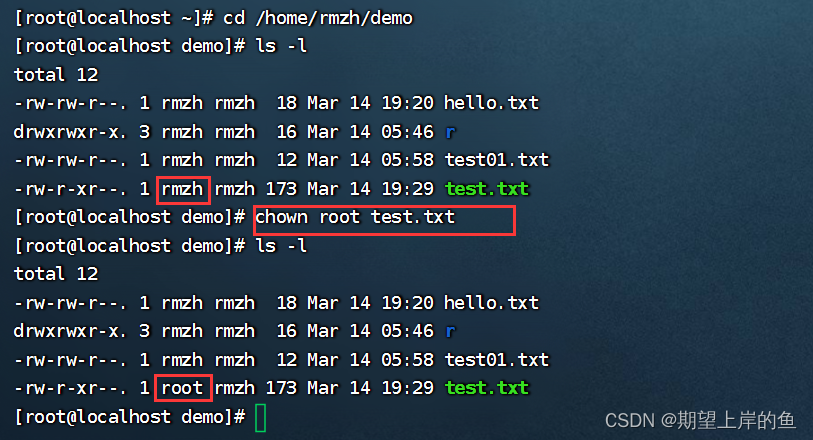
Linux用户和权限 —— 操作演示
Linux用户和权限——操作演示认知root用户用户、用户组管理查看权限控制修改权限控制- chmod修改权限控制- chownLinux系列: Linux基本命令 —— 操作演示 认知root用户 root用户(超级管理员) 无论是Windows、MacOS、Linux均采用多用户的管理模式进行权限管理。…...

【华为OD机试真题2023 JAVA】单核CPU任务调度
华为OD机试真题,2023年度机试题库全覆盖,刷题指南点这里 单核CPU任务调度 知识点队列优先级队列 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 现在有一个CPU和一些任务需要处理,已提前获知每个任务的任务ID、优先级、所需执行时间和到达时间。 CPU同时只…...

News乐鑫科技亮相德国嵌入式展 Embedded World 2023!
3 月 14 日,德国纽伦堡嵌入式展 Embedded World 2023 火热启幕。本届 Embedded World 主题为 “embedded. responsible. sustainable”,乐鑫科技 (688018.SH) 携众多 AIoT 科技成果亮相展会,致力于打造更智能、更互联、更绿色的物联网未来。…...
java如何创建线程
java如何创建线程1. java如何创建线程1.1 通过继承Thread类来创建线程1.2 通过实现Runnable接口来创建线程1.3 通过匿名内部类来创建线程1.4 lambda表达式1.5 通过实现Runnable接口的方式创建线程目标类的优缺点1. java如何创建线程 一个线程在Java中使用一个Thread实例来描述…...

要是早看到这篇文章,你起码少走3年弯路,20年老程序员的忠告
文章目录前言一、程序员的薪资是怎么样的?二、我现在的情况适合做程序员吗?三、大学期间到底应该学些什么?四、工作还是考研?五、总结前言 我是龙叔,一名工作了20多年的退休老程序员。 如果你在工作之前看到这篇文章…...

IP地址的分类
1. 前言 最初设计互联网络时,为了便于寻址以及层次化构造网络,每个IP地址包括两个标识码(ID),即网络ID和主机ID。 同一个物理网络上的所有主机都使用同一个网络ID,网络上的一个主机(包括网络上工…...
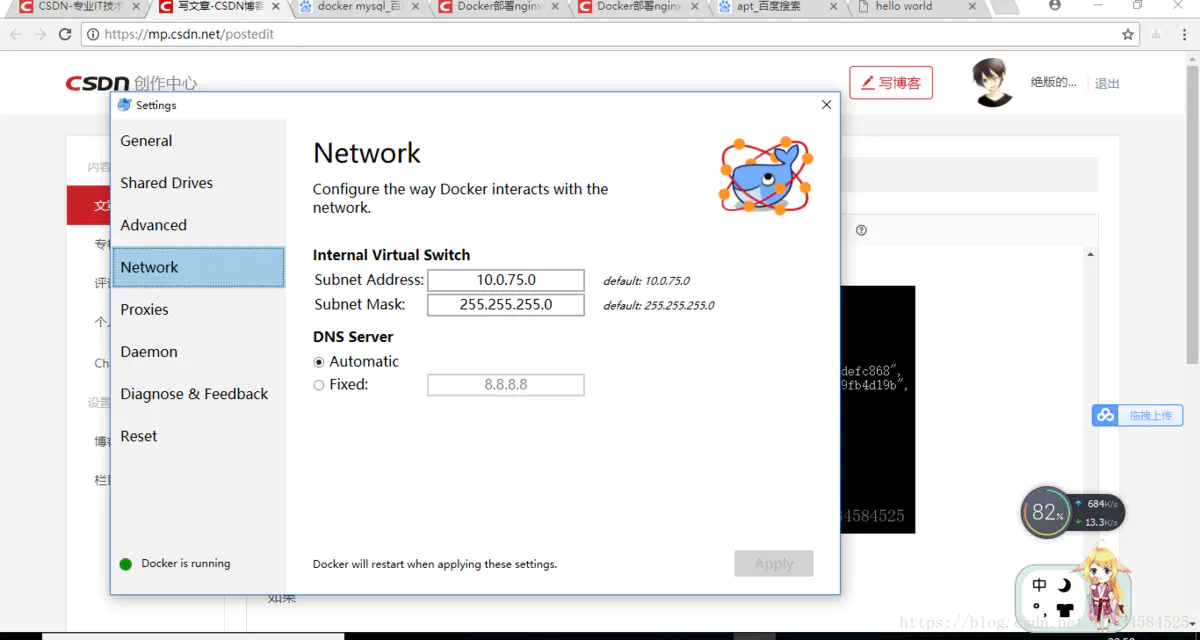
win10下使用docker运行部署nginx,mysql
一、docker的步骤:1.进入docker官网下载安装包2.打开控制面板 - 程序和功能 - 启用或关闭Windows功能,勾选Hyper-V,然后点击确定即可,如图:3.重新启动电脑4.启动Docker在桌面找到Docker for Windows快捷方式࿰…...
sprinboot车辆充电桩
sprinboot车辆充电桩演示录像2022开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:ecli…...
仿京东放大镜效果的实现
仿京东放大镜 (1) 整个案例可以分为三个功能模块 (2) 鼠标经过小图片盒子, 黄色的遮挡层 和 大图片盒子显示,离开隐藏2个盒子功能 (3)黄色的遮挡层跟随鼠标功能。 (4&…...

ESP32设备驱动-LM35温度传感器驱动
LM35温度传感器驱动 文章目录 LM35温度传感器驱动1、LM35介绍2、硬件准备3、软件准备4、驱动实现1、LM35介绍 LM35 系列是精密集成电路温度传感器,其输出电压与摄氏(摄氏度)温度成线性比例。 因此,LM35 优于以开尔文校准的线性温度传感器,因为用户无需从其输出中减去较大…...
基于深度学习的犬种识别软件(YOLOv5清新界面版,Python代码)
摘要:基于深度学习的犬种识别软件用于识别常见多个犬品种,基于YOLOv5算法检测犬种,并通过界面显示记录和管理,智能辅助人们辨别犬种。本文详细介绍博主自主开发的犬种检测系统,在介绍算法原理的同时,给出Py…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
